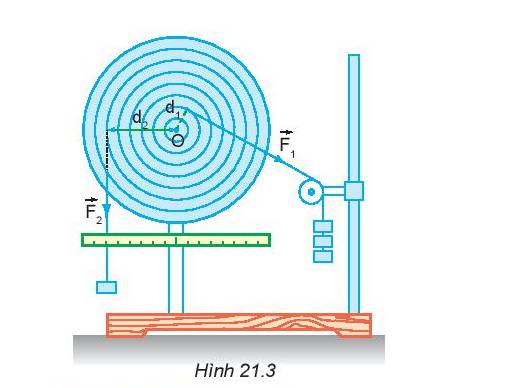
1. Nếu bỏ lực \(\overrightarrow{F_1}\) thì đĩa quay theo chiều nào?
2. Nếu bỏ lực \(\overrightarrow{F_2}\) thì đĩa quay theo chiều nào?
3. Khi đĩa cân bằng lập tích F1.d1 và F2.d2 rồi so sánh.
|
Hình 30.3 mô ta khung dây dẫn ABCD (có thể quay quanh trục OO’) có dòng điện chạy qua đặt trong từ trường, chiều của dòng điện và tên các cực của nam châm đã chỉ rõ trên hình. a) Hãy vẽ lực \(\overrightarrow{F_1}\) tác dụng lên đoạn dây dẫn AB và lực \(\overrightarrow{F_2}\) tác dụng lên đoạn dây CD. |
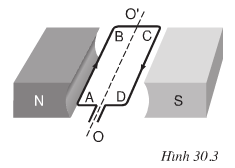 |
b) Cặp lực \(\overrightarrow{F_1}\), \(\overrightarrow{F_2}\) làm cho khung dây quay theo chiều nào?
c) Để cho khung dây ABCD quay theo chiều ngược lại thì phải làm thế nào?
a)Xem hình 30.3b
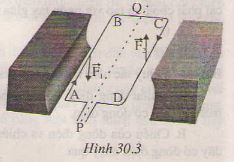
b) Cặp lực \(\overrightarrow{F1}\), \(\overrightarrow{F2}\) làm cho khung dây quay ngược chiều kim đồng hồ.
c)Khung dây quay theo chiều ngược lại khi cặp lực \(\overrightarrow{F1}\), \(\overrightarrow{F2}\) có chiều ngược lại, muốn vậy phải đổi chiều dòng điện trong khung dây hoặc phải đổi chiều từ trường.
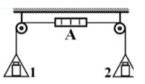
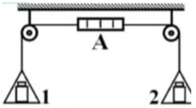
Trong hình vẽ, A là lực kế, mỗi đĩa có một quả cân 3kg thì chỉ số của lực kế A là x. Bỏ qua khối lượng của đĩa cân và của lực kế. Nếu bớt 1kg ở đĩa cân thì số chỉ của lực kế là y. Lấy g = 10m/s2. Giá trị của (x – y) gần giá trị nào nhất sau đây?
A. 35N.
B. 15N.
C. 55N.
D. 8N.
Trong hình vẽ, A là lực kế, mỗi đĩa có một quả cân 3kg thì chỉ số của lực kế A là x. Bỏ qua khối lượng của đĩa cân và của lực kế. Nếu bớt 1kg ở đĩa cân thì số chỉ của lực kế là y. Lấy g = 10m/s2. Giá trị của (x – y) gần giá trị nào nhất sau đây?
A. 35N.
B. 15N.
C. 55N.
D. 8N.
Chọn D.
Lúc đầu, cơ hệ cân bằng, số chỉ lực kế bằng lực căng sợi dây và bằng trọng lượng mỗi đĩa: x = mg = 30N.
Sau đó, hệ chuyển động với gia tốc có độ lớn a, số chỉ lực kế bằng lực căng T:
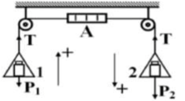
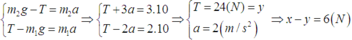
Đĩa cân bên phải có 3 quả cân nặng 600g, 300g, 100g. Đĩa cân bên trái có 2 quả lê và 1 quả táo. Nếu bỏ 1 quả lê và thêm 2 quả táo vào đĩa cân bên trái, muốn hai bên bằng nhau thì cần bỏ quả cân nào ở đĩa cân bên trái. Biết lúc đầu hai bên bằng nhau và 1 quả lê nặng 420g.
2 quả lê 1 quả táo nặng
600+300+100=1000 g
2 quả lê nặng
420x2=840 g
1 quả táo nặng
1000-840=160 g
Nếu bỏ 1 quả lê và thêm 2 quả táo thì đĩa cân bên trái có 1 quả lê và 3 quả táo có khối lượng là
420+3x160=900 g
quả cân phải bỏ ra là
1000-900=100 g
tôi là học sinh lớp 3 hỏi toán lớp 4
Chất điểm A chịu tác động của ba lực \(\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}} ,\;\overrightarrow {{F_3}} \) như hình 4.30 và ở trạng thái cân bằng (tức là \(\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} + \;\overrightarrow {{F_3}} = \overrightarrow 0 \)). Tính độ lớn của các lực \(\overrightarrow {{F_2}} ,\;\overrightarrow {{F_3}} \) biết \(\overrightarrow {{F_1}} \) có độ lớn là 20N.

Tham khảo:
Bước 1: Đặt \(\overrightarrow u = \overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} \). Ta xác định các điểm như hình dưới.

Dễ dàng xác định điểm C, là điểm thứ tư của hình bình hành ABCD. Do đó vecto \(\overrightarrow u \) chính là vecto \(\overrightarrow {AC} \)
Vì chất điểm A ở trang thái cân bằng nên \(\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} + \;\overrightarrow {{F_3}} = \overrightarrow 0 \) hay \(\;\overrightarrow u + \;\overrightarrow {{F_3}} = \overrightarrow 0 \)
\( \Leftrightarrow \;\overrightarrow u \) và \(\;\overrightarrow {{F_3}} \) là hai vecto đối nhau.
\( \Leftrightarrow A\) là trung điểm của EC.
Bước 2:
Ta có: \(\left| {\overrightarrow {{F_1}} } \right| = AD = 20,\;\left| {\overrightarrow {{F_2}} } \right| = AB,\;\left| {\overrightarrow {{F_3}} } \right| = AC.\)
Do A, C, E thẳng hàng nên \(\widehat {CAB} = {180^o} - \widehat {EAB} = {60^o}\)
\(\begin{array}{l} \Rightarrow \widehat {CAD} = {90^o} - {60^o} = {30^o}\\ \Rightarrow \left\{ \begin{array}{l}AC = \frac{{AD}}{{\cos {{30}^o}}} = \frac{{40\sqrt 3 }}{3};\;\\AB = DC = AC.\sin {30^o} = \frac{{20\sqrt 3 }}{3}.\end{array} \right.\end{array}\)
Vậy \(\;\left| {\overrightarrow {{F_2}} } \right| = \frac{{20\sqrt 3 }}{3},\;\;\left| {\overrightarrow {{F_3}} } \right| = \frac{{40\sqrt 3 }}{3}.\)
Hai lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) tác dụng lên một vật. Làm thế nào xác định hợp lực của hai lực này bằng dụng cụ thí nghiệm?
- Xác định xem hai lực đó là lực đồng quy hay hai lực song song, cùng chiều.
- Sử dụng các bộ dụng cụ thí nghiệm thích hợp.

Bài 1 : Tính hợp lực của 2 lực đồng quy F1=16N , F2=12N trong các tường hợp góc hợp bởi hai lực lần lược là
\(\alpha=0^o,\alpha=30^o,\alpha=60^o,\alpha=90^o,\alpha=120^o,\alpha=180^o\)
Trong 4 trường hợp áp dụng
\(F^2=F_1^2+F_1^2+2F_1F_2\cos\)
\(\overrightarrow{F_1}\uparrow\uparrow\overrightarrow{F_2}\Rightarrow F=F_1+F_2\)
\(\overrightarrow{F_1}\uparrow\downarrow\overrightarrow{F_2}\Rightarrow F=F_1-F_2\)
\(\overrightarrow{F_1}L\overrightarrow{F_2}\Rightarrow F=\sqrt{F_1^2+F_2^2}\) chữ ''L'' là vuông góc nha
Bài 2: Một lò xo có chiều dài tự nhiên Lo=12cm khi bị kéo dãn lò xo dài 24cm và lực đàn hồi của nó là 5N .
Hỏi khi lực đàn hồi của lò xo là 10N thì chiều dài của lò xo = bao nhiêu ?
Công thức
\(F_2=K.\Delta l\)
\(=K\left|l-l_o\right|\)
\(F_2=K\left|l_{2_{ }}-lo\right|\)
Bài 3: Một vật trượt trên 1 sàn nằm ngang với vận tốc ban đầu vo=10m/s hệ số ma sát trượt là \(\mu=0,1\) . Hỏi
vật đi được quảng đường = bao nhiêu thì dừng lại cho g=10m/s2
Bài 1:
\(\alpha= 0\) \(\Rightarrow F = F_1+F_2 = 16+12=28N\)
\(\alpha = 30^0\)\(\Rightarrow F^2=16^2+12^2+2.16.12.\cos30^0=...\Rightarrow F\)
Các trường hợp khác bạn tự tính nhé.
Bài 2:
Ta có: \(F_1=k.\Delta \ell_1=k.(0,24-0,12)=0,12.k=5\) (1)
\(F_1=k.\Delta \ell_2=k.(\ell-0,12)=10\) (2)
Lấy (2) chia (1) vế với vế: \(\dfrac{\ell-0,12}{0,12}=2\)
\(\Rightarrow \ell = 0,36m = 36cm\)
Bài 3:
Áp lực lên sàn: \(N=P=mg\)
Áp dụng định luật II Niu tơn ta có: \(F=m.a\Rightarrow -F_{ms}=ma\)
\(\Rightarrow a = \dfrac{-F_{ms}}{m}= \dfrac{-\mu.N}{m}== \dfrac{-\mu.mg}{m}=-\mu .g =- 0,1.10=-1\)(m/s2)
Quãng đường vật đi được đến khi dừng lại là \(S\)
Áp dụng công thức độc lập: \(v^2-v_0^2=2.a.S\)
\(\Rightarrow 0^2-10^2=2.1.S\Rightarrow S = 50m\)
giải nhanh giúp mình trước thứ 3 nha mấy bạn
Bạn đã có các công thức ở trên rồi đó, hãy thay vào công thức và tính thôi nhé.
Hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cho trước cùng tác dụng lên một vật tại điểm O và tạo với nhau một góc \((\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ) = \alpha \) làm cho vật di chuyển theo hướng từ O đến C (Hình 74). Lập công thức tính cường độ của hợp lực \(\overrightarrow F \) làm cho vật di chuyển theo hướng từ O đến C (giả sử chỉ có đúng hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) làm cho vật di chuyển).
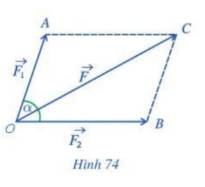
Ta có: \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\;\overrightarrow {{F_2}} = \overrightarrow {OB}= \overrightarrow {AC} \)
Khi đó: Hợp lực \(\overrightarrow F \) là \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \).
Áp dụng định lí cosin cho tam giác OAC, ta có:
\(\begin{array}{*{20}{l}}
{\;\;\;{\mkern 1mu} {\kern 1pt} \;O{C^2} = O{A^2} + A{C^2} - 2.OA.AC.\cos A}\\
\begin{array}{l}
\Leftrightarrow O{C^2} = O{A^2} + A{C^2} - 2.OA.AC.\cos ({180^o} - \alpha )\\
\Leftrightarrow O{C^2} = O{A^2} + A{C^2} + 2.OA.AC.\cos \alpha
\end{array}\\
{ \Leftrightarrow \left| {\vec F} \right| = \sqrt {{{\left| {\overrightarrow {{F_1}} } \right|}^2} + {{\left| {\overrightarrow {{F_2}} } \right|}^2} + 2.\left| {\overrightarrow {{F_1}} } \right|.\left| {\overrightarrow {{F_2}} } \right|.\cos \alpha } }
\end{array}\)
đĩa xích của xe đạp có 50 răng , đĩa líp 20 răng. Tính tỉ số truyền i và cho biết đĩa nào quay nhanh hơn và nhanh hơn bao nhiêu lần. nếu đĩa xích quay với tốc độ 200 vòng/phút thì tốc độ của đĩa líp bằng bao nhiêu?