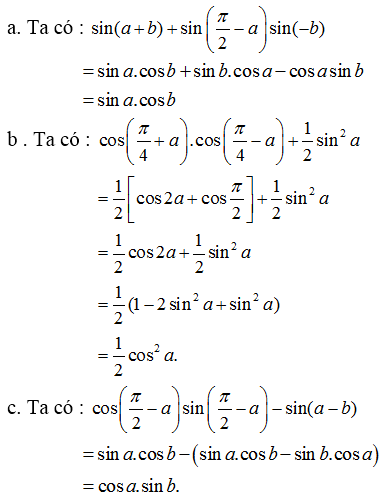rút gọn C=\(\dfrac{cos2a-sin\left(b-a\right)}{2cosa.cosb-cos\left(a-b\right)}\)

Những câu hỏi liên quan
rút gọn: (cos2a-sin(b-a))(2cosa.cosb-cos(a-b))
rút gọn: (cos2a-sin(b-a))(2cosa.cosb-cos(a-b))
Chứng minh các hệ thức sau :
a) sinalpha+sinleft(alpha+dfrac{14}{3}piright)+sinleft(alpha-dfrac{8}{3}piright)0
b) dfrac{sin4a}{1+cos4a}.dfrac{cos2a}{1+cos2a}cotleft(dfrac{3}{2}pi-aright)
c) left(cos a-cos bright)^2-left(sin a-sin bright)^2-4sin^2dfrac{a-b}{2}cosleft(a+bright)
d) sin^2left(45^0+alpharight)-sin^2left(30^0-alpharight)-sin15^0cosleft(15^0+2alpharight)sin2alpha
Đọc tiếp
Chứng minh các hệ thức sau :
a) \(\sin\alpha+\sin\left(\alpha+\dfrac{14}{3}\pi\right)+\sin\left(\alpha-\dfrac{8}{3}\pi\right)=0\)
b) \(\dfrac{\sin4a}{1+\cos4a}.\dfrac{\cos2a}{1+\cos2a}=\cot\left(\dfrac{3}{2}\pi-a\right)\)
c) \(\left(\cos a-\cos b\right)^2-\left(\sin a-\sin b\right)^2=-4\sin^2\dfrac{a-b}{2}\cos\left(a+b\right)\)
d) \(\sin^2\left(45^0+\alpha\right)-\sin^2\left(30^0-\alpha\right)-\sin15^0\cos\left(15^0+2\alpha\right)=\sin2\alpha\)
Rút gọn các biểu thức :
a) \(\sin\left(a+b\right)+\sin\left(\dfrac{\pi}{2}-a\right)\sin\left(-b\right)\)
b) \(\cos\left(\dfrac{\pi}{4}+a\right)\cos\left(\dfrac{\pi}{4}-a\right)+\dfrac{1}{2}\sin^2a\)
c) \(\cos\left(\dfrac{\pi}{2}-a\right)\sin\left(\dfrac{\pi}{2}-b\right)-\sin\left(a-b\right)\)
rút gọn biểu thức:
E=cos(\(\dfrac{3\pi}{3}-\alpha\))-sin(\(\dfrac{3\pi}{2}-\alpha\))+sin(\(\alpha+4\pi\))
Đúng 0
Bình luận (0)
Rút gọn cac biểu thức sau:Asinleft(dfrac{5pi}{2}-alpharight)+cosleft(13pi+alpharight)-3sinleft(alpha-5piright)Bsinleft(x+dfrac{85pi}{2}right)+cosleft(2017pi+xright)+sin^2left(33pi+xright)+sin^2left(x-dfrac{5pi}{2}right)+cosleft(x+dfrac{3pi}{2}right)Csinleft(x+dfrac{2017pi}{2}right)+2sin^2left(x-piright)+cosleft(x+2019piright)+cos2x+sinleft(x+dfrac{9pi}{2}right)
Đọc tiếp
Rút gọn cac biểu thức sau:
\(A=sin\left(\dfrac{5\pi}{2}-\alpha\right)+cos\left(13\pi+\alpha\right)-3sin\left(\alpha-5\pi\right)\)
\(B=sin\left(x+\dfrac{85\pi}{2}\right)+cos\left(2017\pi+x\right)+sin^2\left(33\pi+x\right)+sin^2\left(x-\dfrac{5\pi}{2}\right)+cos\left(x+\dfrac{3\pi}{2}\right)\)\(C=sin\left(x+\dfrac{2017\pi}{2}\right)+2sin^2\left(x-\pi\right)+cos\left(x+2019\pi\right)+cos2x+sin\left(x+\dfrac{9\pi}{2}\right)\)
\(A=sin\left(\dfrac{\pi}{2}-\alpha+2\pi\right)+cos\left(\pi+\alpha+12\pi\right)-3sin\left(\alpha-\pi-4\pi\right)\)
\(=sin\left(\dfrac{\pi}{2}-\alpha\right)+cos\left(\pi+\alpha\right)-3sin\left(\alpha-\pi\right)\)
\(=cos\alpha-cos\alpha+3sin\left(\pi-\alpha\right)\)\(=3sin\alpha\)
\(B=sin\left(x+\dfrac{\pi}{2}+42\pi\right)+cos\left(x+\pi+2016\pi\right)+sin^2\left(x+\pi+32\pi\right)+sin^2\left(x-\dfrac{\pi}{2}-2\pi\right)+cos\left(x-\dfrac{\pi}{2}+2\pi\right)\)
\(=sin\left(x+\dfrac{\pi}{2}\right)+cos\left(x+\pi\right)+sin^2\left(x+\pi\right)+sin^2\left(x-\dfrac{\pi}{2}\right)+cos\left(x-\dfrac{\pi}{2}\right)\)
\(=cosx-cosx+sin^2x+cos^2x+sinx\)
\(=1+sinx\)
\(C=sin\left(x+\dfrac{\pi}{2}+1008\pi\right)+2sin^2\left(\pi-x\right)+cos\left(x+\pi+2018\pi\right)+cos2x+sin\left(x+\dfrac{\pi}{2}+4\pi\right)\)
\(=sin\left(x+\dfrac{\pi}{2}\right)+2sin^2\left(\pi-x\right)+cos\left(x+\pi\right)+cos2x+sin\left(x+\dfrac{\pi}{2}\right)\)
\(=cosx+2sin^2x-cosx+1-2sin^2x+cosx\)
\(=1+cosx\)
Đúng 1
Bình luận (2)
rút gọn: (cos2a-sin(b-a))(2cosa.cosb-cos(a-b))
rút gọn: (cos2a-sin(b-a))(2cosa.cosb-cos(a-b))
Rút gọn biểu thức \(M = \cos \left( {a + b} \right)\cos \left( {a - b} \right) - \sin \left( {a + b} \right)\sin \left( {a - b} \right)\), ta được
A. \(M = \sin 4a\)
B. \(M = 1 - 2{\cos ^2}a\)
C. \(M = 1 - 2{\sin ^2}a\)
D. \(M = \cos 4a\)
\(\cos \left( {a + b} \right)\cos \left( {a - b} \right) - \sin \left( {a + b} \right)\sin \left( {a - b} \right)\)
\( = \frac{1}{2}\left[ {\cos \left( {a + b - a + b} \right) + \cos \left( {a + b + a - b} \right)} \right] - \frac{1}{2}\left[ {\cos \left( {a + b - a + b} \right) - \cos \left( {a + b + a - b} \right)} \right]\)
\( = \frac{1}{2}\left( {\cos 2b + \cos 2a - \cos 2b + \cos 2a} \right) = \frac{1}{2}.2\cos 2a = \cos 2a = 1 - 2{\sin ^2}a\)
Vậy chọn đáp án C
Đúng 0
Bình luận (0)
Sử dụng công thức cộng, rút gọn mỗi biểu thức sau:
\(\cos \left( {a + b} \right) + \cos \left( {a - b} \right);\,\,\cos \left( {a + b} \right) - \cos \left( {a - b} \right);\,\,\sin \left( {a + b} \right) + \sin \left( {a - b} \right)\)
\(\begin{array}{l}\cos \left( {a + b} \right) + \cos \left( {a - b} \right) = \cos a.\cos b - \sin a.\sin b + \sin a.\sin b + \cos a.\cos b = 2\cos a.\cos b\\\cos \left( {a + b} \right) - \cos \left( {a - b} \right) = \cos a.\cos b - \sin a.\sin b - \sin a.\sin b - \cos a.\cos b = - 2\sin a.\sin b\\\sin \left( {a + b} \right) + \sin \left( {a - b} \right) = \sin a.\cos b + \cos a.\sin b + \sin a.\cos b - \cos a.\sin b = 2\sin a.\cos b\end{array}\)
Đúng 0
Bình luận (0)