Cho tứ giác ABCD nội tiếp (O;R) với độ dài các dây AB=R,BC=R\(\sqrt{2}\) ,DC=R\(\sqrt{3}\).Gọi M là giao điểm của hai đường thẳng AD và BC.Khi đó số đo góc AMB là
A.900 B.600 C.450 D.300
Những câu hỏi liên quan
Cho tứ giác ABCD. Gọi O1, O2, O3, O4 là tâm đường tròn nội tiếp tam giác ABD, ABC, BCD, CDA. CMR: Nếu O1O2O3O4 là hình chữ nhật thì tứ giác ABCD là tứ giác nội tiếp
đề sai. muốn c/m đề sai thì nói. mình c/m cho
28 tháng 2 2021 lúc 10:53
Cho tứ giác ABCD, gọi O là giao điểm hai đường chéo và I là giao điểm hai cạnh bên AD và BC. Chứng minh rằng:
a) Tứ giác ABCD nội tiếp khi và chỉ khi OA.OC = OB.OD
b) Tứ giác ABCD nội tiếp khi và chỉ khi IA. ID = IB. IC
a) Chúng ta sẽ dùng cách chứng minh phản chứng
Để ABCD là tứ giác nội tiếp thì OA=OB=OC=OD(O là tâm của đường tròn ngoại tiếp tứ giác nội tiếp ABCD vì O là giao điểm của hai đường chéo)
hay \(OA\cdot OC=OB\cdot OD\)(đpcm)
Đúng 0
Bình luận (1)
Cho tứ giác ABCD nội tiếp (O;r) và ngoại tiếp (O;r').CMR:r≥2√r′
Cho tứ giác ABCD, gọi O là giao điểm hai đường chéo và I là giao điểm hai cạnh bên AD và BC. Chứng minh rằng:
a) Tứ giác ABCD nội tiếp khi và chỉ khi OA.OC = OB.OD
b) Tứ giác ABCD nội tiếp khi và chỉ khi IA. ID = IB. IC
bài này em ko bt em mới học lp 6 thôi
Đúng 0
Bình luận (0)
Cho tứ giác ABCD nội tiếp đường tròn tâm O đường kính AD hai đường chéo AC và BD cắt nhau tại E kẻ EF vuông góc ad a) Chứng minh tứ giác ECDF nội tiếp Xác định tâm I b) Chứng minh CA là phân giác của góc BCF c) Chứng minh tứ giác bcef nội tiếp
a) Xét (O) có
ΔACD nội tiếp đường tròn(A,C,D\(\in\)(O))
AD là đường kính(gt)
Do đó: ΔACD vuông tại C(Định lí)
Suy ra: AC\(\perp\)CD tại C
hay \(EC\perp CD\) tại C
Xét tứ giác ECDF có
\(\widehat{EFD}\) và \(\widehat{ECD}\) là hai góc đối
\(\widehat{EFD}+\widehat{ECD}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ECDF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)
cho tứ giác ABCD nội tiếp đường tròn (O). Chứng minh AB.CD+AD.BC=AC.BD
Ta có: `hat(ABD) = hat(ACD)`.
Lấy `M in AC` sao cho `hat(ADB) = hat(MDC)`.
`=> triangle ABD ~ triangle MCD`.
`=> (AB)/(MC) = (BD)/(CD) => AB . CD = BD . MC`.
Xét `2 triangle ADM, BDC`, ta có:
`hat(ADM) = hat(BDC)`.
`(DA)/(DM) = (BD)/(DC) ( triangle ABD ~ triangle MCD )`.
`=> triangle ADM ~ triangle BCD => (AD)/(AM) = (BD)/(CB) => AD . BC = BD . AM`
`=> AD . BC + AD . BC = BD . AM + BD . MC`
`=> AD . BC + AD . BC = BD(AM+MC)`
`=> AD.BC+AD.BC = BD . AC => dpcm`.
Đúng 3
Bình luận (3)
Cho tứ giác ABCD nội tiếp (O), M là điểm chính giữa của cung AB. Nối M với D, M với C cắt AB lần lượt ở E và P. Chứng minh PEDC là tứ giác nội tiếp
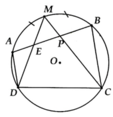
Ta có: A E D ^ = 1 2 s đ A D ⏜ + s đ M B ⏜
= 1 2 s đ D M ⏜ = M C D ^ => D E P ^ + P C D ^ = 180 0
=> PEDC nội tiếp
Đúng 0
Bình luận (0)
Cho tứ giác ABCD, gọi O là giao điểm hai đường chéo và I là giao điểm hai cạnh bên AD và BC. Chứng minh rằng:
a) Tứ giác ABCD nội tiếp khi và chỉ khi OA.OC = OB.OD
b) Tứ giác ABCD nội tiếp khi và chỉ khi IA. ID = IB. IC
Cho tứ giác ABCD nội tiếp đường tròn (O) (hình 1) . Chọn khẳng định sai? A.
B
D
C
^
B
A
C
^
B.
A
B
C
^
+
A
D...
Đọc tiếp
Cho tứ giác ABCD nội tiếp đường tròn (O) (hình 1) . Chọn khẳng định sai?
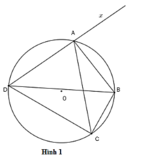
A. B D C ^ = B A C ^
B. A B C ^ + A D C ^ = 180 0
C. B D C ^ = B A x ^
D. B A C ^ = B A x ^
Chọn đáp án D
(góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó )
Phương án A, B, C đúng
Đúng 0
Bình luận (0)
cho tứ giác abcd nội tiếp đt (o). cm rằng: AB.CD+BC.AD=AC.BD
gợi ý:
lúc đầu nó là 1 bdt vì nó nội tiếp nên dấu = xảy ra!
Đúng 0
Bình luận (0)
bđt ptoleme nhé bạn.
Trên cung nhỏ BC, ta có các góc nội tiếp ∠BAC = ∠BDC, và trên cung AB, ∠ADB = ∠ACB
Đúng 0
Bình luận (0)
Giả sử góc ACD > góc ACB. Lấy E trên BD sao cho góc DCE = góc ACB.
Ta có : 2 tam giác ABC và DEC đồng dạng (DCE = ACB; BAC = BDC (chắn cung BC)) => \(\frac{AB}{DE}=\frac{AC}{CD}\) => AB.CD = AC.DE (1)
Tương tự, ta có 2 tam giác ACD và BCE đồng dạng => AD.BC = BE.AC (2)
Từ (1) và (2) => AB.CD + AD.BC = AC.DE + BE.AC hay AB.CD + BC.AD = AC.BD
Đúng 0
Bình luận (0)