Câu c làm sao ạ, trình bày chi tiết giúp em nh

em hãy nêu chi tiết đặc sắc trong văn bản Thánh Gióng và giải thích vì sao chi tiết đó lại là đặc sắc( trình bày thành 1 đoạn văn từ 4-5 câu )
giúp em làm gấp cái ạ mai em kt rùi
Sau khi học bài''Thánh Giong''chi tiết mà làm em thấy hấp dẫn nhát vẫn là chi tiết''Lúc xung trận, khi roi sắt gãy, Gióng nhổ tre bên đường đánh giặc.''Chi tiết này khẳng định rằng: gậy sắt là vũ khí của người anh hùng nhưng khi cần thì cả cỏ cây cũng biến thành vũ khí. Điều đó thể hiện sự linh hoạt, sáng tạo trong chiến đấu của nhân dân ta. Trong nhiều cuộc kháng chiến chống ngoại xâm, cha ông ta đã dùng đến cả gậy tầm vông, giáo mác, cày, cuốc,... để đối chọi với súng ống, xe tăng của giặc. Và cuối cùng Gióng đánh giặc xong, cởi áo giáp sắt để lại và bay thẳng lên trời.
Mọi người giúp em câu 1 với ạ trình bày chi tiết giúp em luôn ạ (em đang cần gấp)
Câu 1:
\(\left\{{}\begin{matrix}y-2x< =2\\2y-x>=4\\x+y< =5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y< =2x+2\\2y>=x+4\\y< =-x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y< =2x+2\\y< =-x+5\\y>=\dfrac{1}{2}x+2\end{matrix}\right.\)
y<=2x+2
=>y-2x-2<=0
Vẽ đường thẳng y=2x+2
Khi x=0 và y=0 thì \(y-2x-2=0-0-2=-2< =0\)(đúng)
=>Miền nghiệm của BPT y<=2x+2 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y<=-x+5
=>x+y-5<=0
Khi x=0 và y=0 thì \(x+y-5=0+0-5< =0\)(đúng)
=>Miền nghiệm của BPT y<=-x+5 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y>=1/2x+2
=>\(-\dfrac{1}{2}x+y-2>=0\)
Khi x=0 và y=0 thì \(-\dfrac{1}{2}x+y-2=-\dfrac{1}{2}\cdot0+0-2=-2< 0\)
=>O(0;0) không thỏa mãn BPT \(-\dfrac{1}{2}x+y-2>=0\)
=>Miền nghiệm của BPT \(y>=\dfrac{1}{2}x+2\) là nửa mặt phẳng chứa biên nhưng không chứa điểm O(0;0)
Vẽ đồ thị:
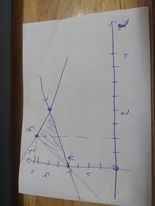
Theo hình vẽ, ta có: Miền nghiệm của hệ BPT sẽ là ΔABC, với A(0;2); B(1;4); C(2;3)
Khi x=0 và y=2 thì F=2-0=2
Khi x=1 và y=4 thì F=4-1=3
Khi x=2 và y=3 thì F=3-2=1
=>Chọn A
Trình bày tự luận chi tiết dẽ hiểu giúp em câu 1208 với ạ
d nhận \(\overrightarrow{u}=\left(1;-1;2\right)\) là 1 vtcp và (P) nhận \(\overrightarrow{n}=\left(1;2;-2\right)\) là 1 vtpt
Ta có: \(\overrightarrow{a}=\left[\overrightarrow{u};\overrightarrow{n}\right]=\left(-2;4;3\right)\)
\(\Rightarrow\left[\overrightarrow{a};\overrightarrow{n}\right]=\left(-14;-1;-8\right)=-1\left(14;1;8\right)\)
Phương trình d dạng tham số: \(\left\{{}\begin{matrix}x=t\\y=-t\\z=2t+1\end{matrix}\right.\)
Gọi M là giao điểm d và (P), tọa độ M thỏa:
\(t+2\left(-t\right)-2\left(2t+1\right)+2=0\Rightarrow t=0\Rightarrow M\left(0;0;1\right)\)
Hình chiếu vuông góc của d lên (P) nhân (14;1;8) là 1 vtpt và đi qua M nên có dạng:
\(\dfrac{x}{14}=\dfrac{y}{1}=\dfrac{z-1}{8}\)
Câu 1. Trình bày và phân tích quyền lợi, trách nhiệm đoàn viên( càng dài càng chi tiết giúp em ạ)
Giúp em trình bày chi tiết ạ em cảm ơn
\(y=\dfrac{x-1}{x+2}\left(x\ne-2\right)\Rightarrow y'=\dfrac{\left(x+2\right)-\left(x-1\right)}{\left(x+2\right)^2}=\dfrac{3}{\left(x+2\right)^2}\)
Giả sử d là tiếp tuyến cần tìm của đths trên
a. d đi qua \(N\left(-1;-2\right)\) . Suy ra : HSG của d : \(\dfrac{3}{\left(-1+2\right)^2}=3\)
PTTT d : \(y=3\left(x+1\right)-2=3x+1\)
b.d có hđtđ \(x_o=3\) \(\Rightarrow y_o=\dfrac{3-1}{3+2}=\dfrac{2}{5};y'=\dfrac{3}{25}\)
PTTT d : \(y=\dfrac{3}{25}\left(x-3\right)+\dfrac{2}{5}=\dfrac{3x}{25}+\dfrac{1}{25}\)
c. Tung độ tiếp điểm yo = 9 nên : \(\dfrac{x_o-1}{x_o+2}=9\Leftrightarrow x_o=-\dfrac{19}{8}\)
y' = 64/3
PTTT d : \(y=\dfrac{64}{3}\left(x+\dfrac{19}{8}\right)+9=\dfrac{64}{3}x+\dfrac{179}{3}\)
d. Ta có : \(\dfrac{3}{\left(x_o+2\right)^2}=\dfrac{1}{3}\Leftrightarrow\left[{}\begin{matrix}x_o+2=3\\x_o+2=-3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x_o=1\\x_o=-5\end{matrix}\right.\)
Với xo = 1 \(\Rightarrow y_o=0\) . PTTT d : y = 1/3(x-1) = 1/3x - 1/3
Với xo = -5 \(\Rightarrow y_o=2\) . PTTT d : \(y=\dfrac{1}{3}\left(x+5\right)+2=\dfrac{1}{3}x+\dfrac{11}{3}\)
Giúp e trình bày chi tiết câu 8 đi ạ 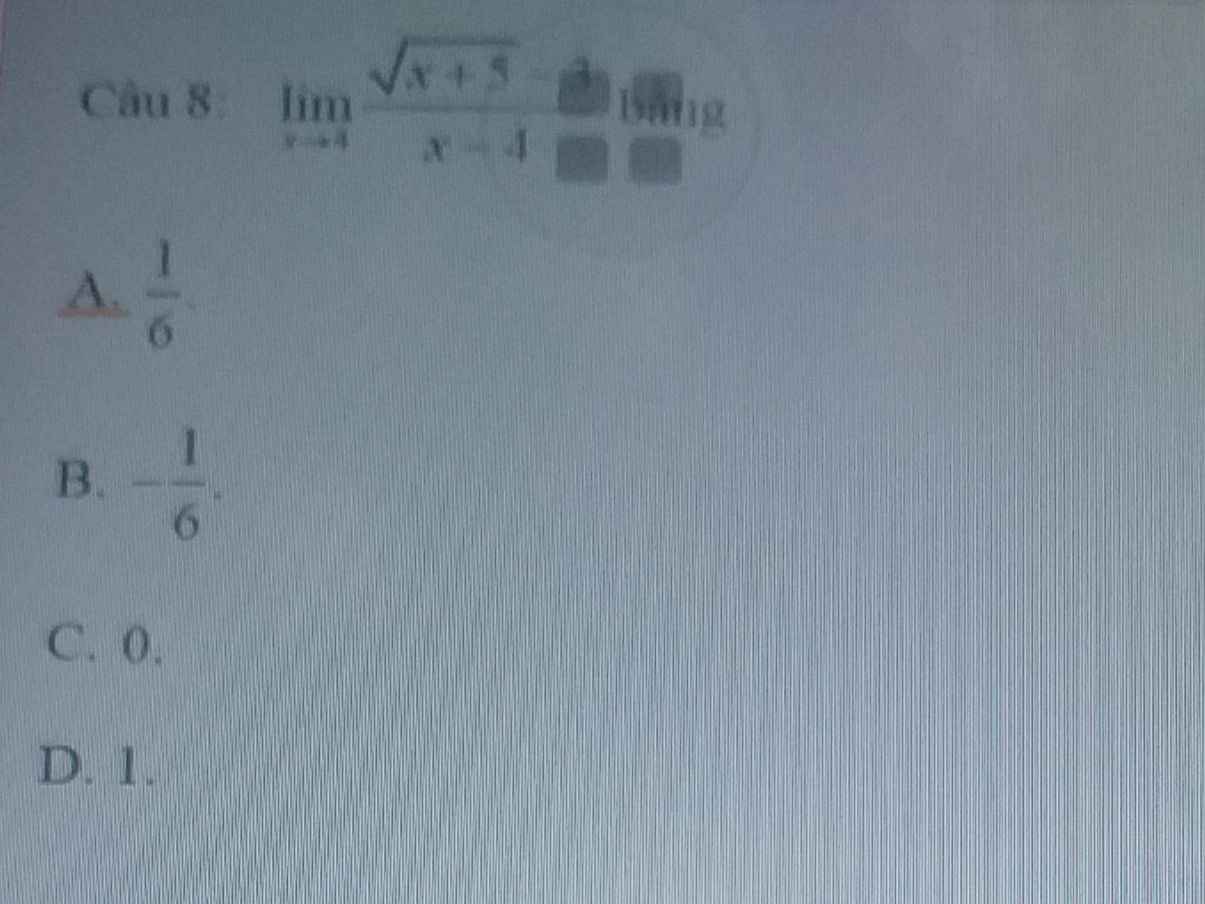
\(\lim\limits_{x\rightarrow4}\dfrac{\sqrt{x+5}-3}{x-4}=\lim\limits_{x\rightarrow4}\dfrac{\left(\sqrt{x+5}-3\right)\left(\sqrt{x+5}+3\right)}{\left(x-4\right)\left(\sqrt{x+5}+3\right)}\)
\(=\lim\limits_{x\rightarrow4}\dfrac{x-4}{\left(x-4\right)\left(\sqrt{x+5}+3\right)}=\lim\limits_{x\rightarrow4}\dfrac{1}{\sqrt{x+5}+3}=\dfrac{1}{3+3}=\dfrac{1}{6}\)

làm bài 6 thôi
trình bày chi tiết giúp với ạ
Bài 6:
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
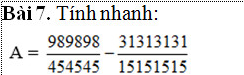
Trình bày chi tiết giúp em với ạ!Em cảm ơn
`(989898)/(454545)` – `(31313131)/(15151515)`
= `(98.10101)/(45.10101)` – `(31.1010101)/(15.1010101)`
= `(98)/(45)` – `(31)/(15)` = `(1)/(9)`
Bài toán này rút gọn phân số nhé cậu
=> A = \(\dfrac{98}{45}\)- \(\dfrac{31}{15}\)=> A = \(\dfrac{98}{45}\)-\(\dfrac{93}{45}\)=> A = \(\dfrac{5}{45}\)= \(\dfrac{1}{9}\)
P/s 989898/454545 mình rút gọn cho 10101
P/s 31313131/15151515 mình rút gọn cho 1010101

giải, trình bày và vẽ hình chi tiết giúp em ạ
Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)