Tìm các giá trị nguyên x để biểu thức A= 3x+1/x+2 nhận giá trị nguyên

Những câu hỏi liên quan
Cho biểu thức
M=căn x +1/2
A)Tìm các giá trị nguyên của x để M nhận giá trị nguyên
B)Tìm giá trị lớn nhất của biểu thức M
c)Tìm các giá trị nguyên của x để A nhận giá trị nguyên
Bài1: Cho biểu thức:
A= x^3 - 3x^2 + 4x - 1 / x-3
a) Tìm điều kiện xác định
b) Tìm giá trị nguyên của x để biểu thức có giá trị nguyên.
Bài 2:Cho biểu thức:
P= x^3 - 3x^2 + 6 / x^2 - 3x
a) Tìm điều kiện xác định
b) Tính giá trị của P khi x = 2
c) Tìm giá trị nguyên của x để P nhận giá trị nguyên
BÀI 1:
a) \(ĐKXĐ:\) \(x-3\)\(\ne\)\(0\)
\(\Leftrightarrow\)\(x\)\(\ne\)\(3\)
b) \(A=\frac{x^3-3x^2+4x-1}{x-3}\)
\(=\frac{\left(x^3-3x^2\right)+\left(4x-12\right)+11}{x-3}\)
\(=\frac{x^2\left(x-3\right)+4\left(x-3\right)+11}{x-3}\)
\(=x^2+4+\frac{11}{x-3}\)
Để \(A\)có giá trị nguyên thì \(\frac{11}{x-3}\)có giá trị nguyên
hay \(x-3\)\(\notinƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
Ta lập bảng sau
\(x-3\) \(-11\) \(-1\) \(1\) \(11\)
\(x\) \(-8\) \(2\) \(4\) \(14\)
Vậy....
Đúng 0
Bình luận (0)
cảm ơn bạn nha nhưng bạn có chắc là nó đúng ko
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho biểu thức B = \(\dfrac{x+1}{x}+\dfrac{2}{1-x}+\dfrac{3x+1}{x^2-x}\)
a) Rút gọn B
b) Tìm B biết |x| = 1
c) Tìm các giá trị nguyên của x để B nhận giá trị nguyên.
a: \(B=\dfrac{x^2-1-2x+3x+1}{x\left(x-1\right)}=\dfrac{x^2+x}{x\left(x-1\right)}=\dfrac{x+1}{x-1}\)
Đúng 2
Bình luận (0)
a) B = \(\dfrac{x+1}{x}-\dfrac{2}{x-1}+\dfrac{3x+1}{x\left(x-1\right)}\) (ĐK: \(x\ne0;1\))
= \(\dfrac{\left(x+1\right)\left(x-1\right)}{x\left(x-1\right)}-\dfrac{2x}{x\left(x-1\right)}+\dfrac{3x+1}{x\left(x-1\right)}\)
= \(\dfrac{x^2-1-2x+3x+1}{x\left(x-1\right)}=\dfrac{x^2+x}{x\left(x-1\right)}=\dfrac{x+1}{x-1}\)
b) \(\left|x\right|=1< =>\left[{}\begin{matrix}x=1\left(L\right)\\x=-1\left(C\right)\end{matrix}\right.\)
Thay x = -1 vào B, ta có:
\(\dfrac{-1+1}{-1-1}=0\)
c) B nguyên <=> \(\dfrac{x+1}{x-1}\) nguyên <=> \(1+\dfrac{2}{x-1}\) nguyên
<=> 2\(⋮x-1\)
<=> x-1 \(\in\left\{-2;-1;1;2\right\}\)
| x-1 | -2 | -1 | 1 | 2 |
| x | -1 | 0 | 2 | 3 |
| C | L | C | C |
KL: x \(\in\left\{-1;2;3\right\}\)
Đúng 2
Bình luận (0)
a) Tìm các giá trị nguyên của x để biểu thức Mdfrac{8x+1}{4x-1}nhận giá trị nguyênb) Tìm giá trị nguyên của biến x để biểu thức Adfrac{5}{4-x}có giá trị lớn nhấtc) Tìm giá trị nguyên của biến x để biểu thức Bdfrac{8-x}{x-3}có giá trị nhỏ nhất(Hơi khó mọi người giúp mình với ạ)
Đọc tiếp
a) Tìm các giá trị nguyên của \(x\) để biểu thức M=\(\dfrac{8x+1}{4x-1}\)nhận giá trị nguyên
b) Tìm giá trị nguyên của biến \(x\) để biểu thức \(A=\dfrac{5}{4-x}\)có giá trị lớn nhất
c) Tìm giá trị nguyên của biến \(x\) để biểu thức \(B=\dfrac{8-x}{x-3}\)có giá trị nhỏ nhất
(Hơi khó mọi người giúp mình với ạ)
a) Ta có: \(M=\dfrac{8x+1}{4x-5}=\dfrac{8x-10+11}{4x-5}=\dfrac{2\left(x-5\right)+11}{4x-5}=2+\dfrac{11}{4x-5}\)
Để M nhận giá trị nguyên thì \(2+\dfrac{11}{4x-5}\) nhận giá trị nguyên
\(\Rightarrow\dfrac{11}{4x-5}\) nhận giá trị nguyên
\(\Rightarrow11⋮4x-5\)
Vì \(x\in Z\) nên \(4x-5\in Z\)
\(\Rightarrow4x-5\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
\(\Rightarrow x\in\left\{1;\pm1,5;4\right\}\)
Vậy \(x\in\left\{1;4\right\}\) thỏa mãn \(x\in Z\).
b) Ta có: \(A=\dfrac{5}{4-x}\). ĐK: \(x\ne4\)
Nếu 4 - x < 0 thì x > 4 \(\Rightarrow A>0\)
4 - x > 0 thì x < 4 \(\Rightarrow A< 0\)
Để A đạt GTLN thì 4 - x là số nguyên dương nhỏ nhất
\(\Rightarrow4-x=1\Rightarrow x=3\)
\(\Rightarrow A=\dfrac{5}{4-3}=5\)
Vậy MaxA = 5 tại x = 3
c) \(B=\dfrac{8-x}{x-3}\). ĐK: \(x\ne3\).
Ta có: \(B=\dfrac{8-x}{x-3}=\dfrac{-\left(x-8\right)}{x-3}=\dfrac{-\left(x-3\right)+5}{x-3}=\dfrac{5}{x-3}-1\)
Để B đạt giá trị nhỏ nhất thì \(\dfrac{5}{x-3}-1\) nhỏ nhất
\(\Rightarrow\dfrac{5}{x-3}\) nhỏ nhất
Nếu x - 3 > 0 thì x > 3 \(\Rightarrow\dfrac{5}{x-3}>0\)
x - 3 < 0 thì x < 3 \(\Rightarrow\dfrac{5}{x-3}< 0\)
Để \(\dfrac{5}{x-3}\) nhỏ nhất thì x - 3 là số nguyên âm lớn nhất
\(\Rightarrow x-3=-1\Rightarrow x=2\)
\(\Rightarrow B=\dfrac{8-2}{2-3}=-6\)
Vậy MaxB = -6 tại x = 2.
Đúng 1
Bình luận (1)
a) Để M nhận giá trị nguyên thì \(8x+1⋮4x-1\)
\(\Leftrightarrow8x-2+3⋮4x-1\)
mà \(8x-2⋮4x-1\)
nên \(3⋮4x-1\)
\(\Leftrightarrow4x-1\inƯ\left(3\right)\)
\(\Leftrightarrow4x-1\in\left\{1;-1;3;-3\right\}\)
\(\Leftrightarrow4x\in\left\{2;0;4;-2\right\}\)
\(\Leftrightarrow x\in\left\{\dfrac{1}{2};0;1;-\dfrac{1}{2}\right\}\)
mà x là số nguyên
nên \(x\in\left\{0;1\right\}\)
Vậy: \(x\in\left\{0;1\right\}\)
Đúng 0
Bình luận (0)
Cho biểu thức: A = (x/x^2-4-4/2-x+1/x+2):3x+3/x^2+2x
a) Tìm điều kiện xác định của A và rút gọn biểu thức A;
b) Tính giá trị của biểu thức A khi |2x-3|-x+1=0
c) Tìm giá trị nguyên của x để A nhận giá trị nguyên.
a: \(A=\left(\dfrac{x}{x^2-4}+\dfrac{4}{x-2}+\dfrac{1}{x+2}\right):\dfrac{3x+3}{x^2+2x}\)
\(=\dfrac{x+4x+8+x-2}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x\left(x+2\right)}{3\left(x+1\right)}\)
\(=\dfrac{6\left(x+1\right)\cdot x\left(x+2\right)}{3\left(x+1\right)\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x}{x-2}\)
Đúng 1
Bình luận (0)
Cho biểu thức A = \(\frac{3x^2+3x-3}{x^2+x-2}-\frac{x+1}{x+2}+\frac{x-2}{x}\times\left(\frac{1}{1-x}-1\right)\)
a) Rút gọn biểu thức A
b) Tìm các giá trị nguyên của x để A nhận giá trị nguyên
c) Tìm x sao cho A < 0
a) A = \(\frac{3x^2+3x-3}{x^2+x-2}-\frac{x+1}{x+2}+\frac{x-2}{x}\cdot\left(\frac{1}{1-x}-1\right)\)
A = \(\frac{3x^2+3x-3}{x^2+2x-x-2}-\frac{x+1}{x+2}+\frac{x-2}{x}\cdot\left(\frac{1-1+x}{1-x}\right)\)
A = \(\frac{3x^2+3x-3}{\left(x-1\right)\left(x+2\right)}-\frac{x+1}{x+2}+\frac{x-2}{x}\cdot\frac{x}{1-x}\)
A = \(\frac{3x^2+3x-3}{\left(x-1\right)\left(x+2\right)}-\frac{x+1}{x+2}-\frac{x-2}{x-1}\)
A = \(\frac{3x^2+3x-3}{\left(x-1\right)\left(x+2\right)}-\frac{\left(x+1\right)\left(x-1\right)}{\left(x-1\right)\left(x+2\right)}-\frac{\left(x-2\right)\left(x+2\right)}{\left(x-1\right)\left(x+2\right)}\)
A = \(\frac{3x^2+3x-3-x^2+1-x^2+4}{\left(x-1\right)\left(x+2\right)}\)
A = \(\frac{x^2+3x+2}{\left(x-1\right)\left(x+2\right)}\)
A = \(\frac{x^2+2x+x+2}{\left(x-1\right)\left(x+2\right)}\)
A = \(\frac{\left(x+1\right)\left(x+2\right)}{\left(x-1\right)\left(x+2\right)}\)
A = \(\frac{x+1}{x-1}\) (Đk: \(x-1\ge0\) => x \(\ge\)1)
b) Ta có: A = \(\frac{x+1}{x-1}=\frac{\left(x-1\right)+2}{x-1}=1+\frac{2}{x-1}\)
Để A \(\in\)Z <=> 2 \(⋮\)x - 1
<=> x - 1 \(\in\)Ư(2) = {1; -1; 2; -2}
<=> x \(\in\){2; 0; 3; -1}
c) Ta có: A < 0
=> \(\frac{x+1}{x-1}< 0\)
=> \(\hept{\begin{cases}x+1< 0\\x-1>0\end{cases}}\) hoặc \(\hept{\begin{cases}x+1>0\\x-1< 0\end{cases}}\)
=> \(\hept{\begin{cases}x< -1\\x>1\end{cases}}\)(loại) hoặc \(\hept{\begin{cases}x>-1\\x< 1\end{cases}}\)
=> -1 < x < 1
Edogawa Conan
Thiếu dòng đầu \(ĐKXĐ:\hept{\begin{cases}x\ne1\\x\ne-2\\x\ne0\end{cases}}\)
ĐKXĐ : \(\) x # +1 ; x # - 1 ; x # -2 ; x # 0 ; x # 2
Ta có: \(A=\frac{3x^2+3x-3}{x^2+x-2}-\frac{x+1}{x+2}+\frac{x-2}{x}.\left(\frac{1}{1-x}-1\right)\)
\(=\frac{3x^2+3x-3}{x^2+x-2}-\frac{x+1}{x+2}+\frac{x-2}{x}.\frac{x}{1-x}\)
\(=\frac{3x^2+3x-3}{x^2+x-2}-\frac{x+1}{x+2}+\frac{x-2}{1-x}\)
\(=\frac{3x^2+3x-3}{x^2+x-2}-\left(\frac{x+1}{x+2}+\frac{x-2}{x-1}\right)\)
\(=\frac{3x^2+3x-3}{x^2+x-2}-\frac{2x^2-5}{x^2+x-2}\)
\(=\frac{x^2+3x+2}{x^2+x-2}=\frac{\left(x+1\right)\left(x+2\right)}{\left(x-1\right)\left(x+2\right)}\)
\(\frac{x+1}{x-1}\)
b. Ta có: \(A=\frac{x+1}{x-1}=\frac{x-1+2}{x-1}=1+\frac{2}{x-1}\)
Để A nhận giá trị nguyên thì: \(2⋮\left(x-1\right)\Rightarrow\left(x-1\right)\inƯ\left(2\right)\)
+) x - 1 = 1 => x = 2 (loại)
+) x - 1 = 2 => x = 3
+) x - 1 = -1 => x = 0 (loại)
+) x - 1 = -2 => x = -1 (loại)
Vậy x = 3 là giá trị cần tìm.
c. \(A< 0\Leftrightarrow\frac{x+1}{x-1}< 0\)
\(\Leftrightarrow\hept{\begin{cases}x+1>0\\x-1< 0\end{cases}}\) hoặc \(\hept{\begin{cases}x+1< 0\\x-1>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>-1\\x< 1\end{cases}}\) hoặc \(\hept{\begin{cases}x< -1\\x>1\end{cases}}\)(vô lý)
Vậy \(-1< x< 1\) và x # 0 là giá trị cần tìm
Cho biểu thức A = 2x mũ 2 + 3x+3/2x+1. Tìm giá trị nguyễn x để A nhận giá trị nguyên
Ta có : \(ĐKXĐ:x\ne-\frac{1}{2}\)
\(A=\left(x+1\right)+\frac{2}{2x+1}\) vì \(x\in Z\) nên A nguyên thì \(\frac{2}{2x+1}\) nguyên
Hay \(2x+1\) là ước của 2 . Nên :
\(2x+1=2\Rightarrow x=\frac{1}{2}\) ( loại )
\(2x+1=1\Rightarrow x=0\) ( t/m)
\(2x+1=-1\Rightarrow x=-1\) ( t/m)
\(2x+1=-2\Rightarrow x=-\frac{3}{2}\) ( loại )
Với \(x=0;x=-1\) thì A nhận giá trị nguyên
Chúc bạn học tốt !!!
Đúng 0
Bình luận (0)
Cho biểu thức: \(A=\left(\frac{2}{3x}-\frac{2}{x+1}.\left(\frac{x+1}{3x}-x-1\right)\right):\frac{x-1}{x}\)
a) Rút gọn biểu thức A
b) Tìm giá trị nguyên của x để A nhận giá trị nguyên
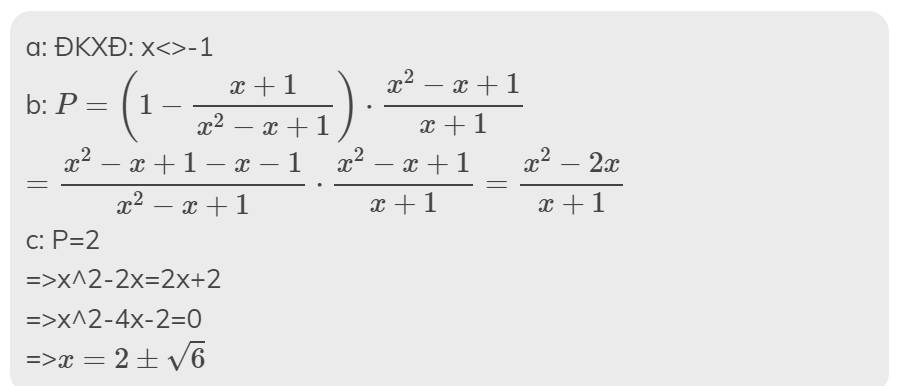
P = \(\left(1-\dfrac{x^2}{x^2-x+1}\right):\dfrac{x^2+2x+1}{x^3+1}\)
a)Tìm điều kiện của x để biểu thức P xác định
b)Rút gọn biểu thức P
c)Với giá trị nào của x thì P = 2
d)Tìm các giá trị nguyên của x để P nhận giá trị nguyên











![[MINT HANOUE]](https://hoc24.vn/images/avt/avt83544866_256by256.jpg)