
Những câu hỏi liên quan
Cho hình bình hành ABCD có cạnh AB = CD = 25m; xác định vị trí của điểm E trên cạnh AB sao cho diện tích hình thang AECD gấp 4 lần diện tích tam giác EBC.
(hình ảnh chỉ mang tính chất minh họa)
Xem chi tiết
Cho hình bình hành ABCD có CD 4cm, đường cao vẽ từ A đến cạnh CD bằng 3cm. Gọi M là trung điểm của AB. DM cắt AC tại N. Tính diện tích hình bình hành ABCD, diện tích tam giác ADM A.
S
A
B
C
D
12
c
m
2
;
S
A
D
M...
Đọc tiếp
Cho hình bình hành ABCD có CD = 4cm, đường cao vẽ từ A đến cạnh CD bằng 3cm. Gọi M là trung điểm của AB. DM cắt AC tại N. Tính diện tích hình bình hành ABCD, diện tích tam giác ADM
A. S A B C D = 12 c m 2 ; S A D M = 3 c m 2
B. S A B C D = 12 c m 2 ; S A D M = 6 c m 2
C. S A B C D = 24 c m 2 ; S A D M = 3 c m 2
D. S A B C D = 24 c m 2 ; S A D M = 6 c m 2
SABCD = AH.CD = 4.3 = 12(cm2)
Vì M là trung điểm của AB nên AM = 1 2 AB = 1 2 .4 = 2(cm)
Ta có chiều cao từ đỉnh D đến cạnh AM của tam giác ADM bằng chiều cao AH của hình bình hành.
=> SADM = 1 2 AH.AM = 1 2 .3.2 = 3(cm2)
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có AB = 12 cm, BC = 8 cm, AH = 6 cm (AH là đường cao ứng với cạnh CD). Tính chu vi và diện tích của hình bình hành ABCD
Chu vi hình bình hành ABCD là:
\(\left(12+8\right)\times2=40\left(cm\right)\)
Diện tích hình bình hành ABCD là:
\(12\times6=72\left(cm^2\right)\)
Giải
Chu vi hình bình hành ABCD đó là :
\(\left(12+8\right)\times2=40\) ( cm )
Diện tích hình bình hành ABCD đó là :
\(12\times6=72\)( cm2 )
Đáp số : Chu vi : \(40\)cm ; Diện tích : \(72\)cm2
Cho hình bình hành ABCD. Trên cạnh AB lấy điểm M, trên cạnh CD lấy điểm N sao cho AM=CN
a, CM AMCN là hình bình hành
b, CM DMBN là hình bình hành
a: Xét tứ giác AMCN có
AM//NC
AM=CN
=>AMCN là hình bình hành
b:
AM+MB=AB
CN+ND=CD
mà AM=CN và AB=CD
nên MB=ND
Xét tứ giác DMBN có
BM//DN
BM=DN
=>DMBN là hình bình hành
Đúng 1
Bình luận (0)
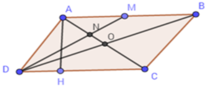
Cho hình bình hành MNPQ có các đỉnh M, N, P, Q laanf lượt nằm trên các cạnh AB, BC, CD, DA của hình bình hành ABCD
Chứng minh rằng hai hình bình hành đó có cùng tâm O.
hình bình hành abcd có độ dài cạnh ab là 8dm độ dài cạnh cd là 6dm chu vi của hình bình hành đó là
Chu vi của hình bình hành ABCD là :
(8 + 6) x 2 = 28 (dm)
Đ/S : 28 dm
= Công thức C = (A+B) X 2. Đúng thì k nhé!
hình bình hành abcd có độ dài cạnh cd là 25m,chiều ao ah là 12 cm . lấy m là trung điểm ab.tính
a diện tích hình thang amcd
b diện tích hình tam giác mbc
a) Vì ABCD là hình bình hành nên AB=CD=25cm.
=>AM=BM=25:2=12,5(cm)(1)
S hình thang AMCD là:
\(\frac{\left(25+12,5\right)\cdot12}{2}=225\left(cm^2\right)\)
b)Vì AH và BH cùng là chiều cao nên AH=BH=12cm
Từ (1), suy ra S hình tam giác MBC là:
\(\frac{12,5\cdot12}{2}=75\left(cm^2\right)\)
đ/s
Cho hình thang ABCD có AB//CD và AB=1/2CD. Gọi E là trung điểm của cạnh CD. Chứng minh các tứ giác ABED,ABCE là các hình bình hành
Ta có: \(AB=\dfrac{1}{2}CD\)(gt)
mà \(ED=EC=\dfrac{CD}{2}\)(E là trung điểm của CD)
nên AB=ED=EC
Xét tứ giác ABED có
AB//DE
AB=DE(cmt)
Do đó: ABED là hình bình hành
Xét tứ giác ABCE có
AB//CE
AB=CE
Do đó: ABCE là hình bình hành
Đúng 0
Bình luận (0)
- Do E là trung điểm của CD
\(=>DE=CE=\dfrac{CD}{2}\)
Mà \(AB=\dfrac{1}{2}CD\) (gt)
\(=>AB=DE=CD\)
- DE và CE trùng CD, AB // CD => AB // DE // CE
Tứ giác ABED có:
- AB=DE (cmt)
- AB // DE (cmt)
Vậy: Tứ giác ABED là hình bình hành (đpcm)
- Tương tự: Tứ giác ABCE có
- AB=CE (cmt)
- AB // CE (cmt)
Vậy tứ giác ABCE là hình bình hành (đpcm)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD ( AB//CD ) có AB CD 4cm, độ dài đường cao hình bình hành là h 2cm. Diện tích của hình bình hành là? A. 4
c
m
2
B. 8
c
m
2
C. 6
c
m
2
D. 3
c
m
2
Đọc tiếp
Cho hình bình hành ABCD ( AB//CD ) có AB = CD = 4cm, độ dài đường cao hình bình hành là h = 2cm. Diện tích của hình bình hành là?
A. 4 c m 2
B. 8 c m 2
C. 6 c m 2
D. 3 c m 2
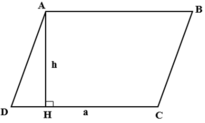
Ta có : S = a.h
Khi đó ta có: S = 4.2 = 8 c m 2 .
Chọn đáp án B.
Đúng 1
Bình luận (0)




















