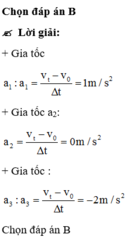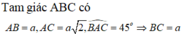Gọi A1,A2,A3 lần lượt là hình chiếu vuông góc của A=(-1;2;3) lên các mặt phẳng (oxy),(oxz),(oyz) phương trình mặt phẳng(A1A2A3) là?

Những câu hỏi liên quan
Gọi A1,A2,A3 lần lượt là hình chiếu vuông góc của A=(-1;2;3) lên các mặt phẳng (oxy),(oxz),(oyz) phương trình mặt phẳng(A1A2A3) là?
Trong không gian Oxyz, gọi
A
1
,
A
2
,
A
3
lần lượt là hình chiếu vuông góc của điểm A(4;3;2) trên các trục Ox, Oy, Oz. Trong các khẳng định sau, khẳng định nào sai? A.
OA
→
OA
1
→
+...
Đọc tiếp
Trong không gian Oxyz, gọi A 1 , A 2 , A 3 lần lượt là hình chiếu vuông góc của điểm A(4;3;2) trên các trục Ox, Oy, Oz. Trong các khẳng định sau, khẳng định nào sai?
A. OA → = OA 1 → + OA 2 → + OA 3 →
B. Phương trình mặt phẳng A 1 A 2 A 3 là x 4 + y 3 + z 2 = 1
C. Thể tích của tứ diện OA 1 A 2 A 3 bằng 4
D. Mặt phẳng ( A 1 A 2 A 3 ) đi qua điểm A
Đáp án C
Vì A 1 , A 2 , A 3 lần lượt là hình chiếu vuông góc của điểm A(4;3;2) lên các trục Ox, Oy, Oz nên ta có A 1 (4; 0; 0), A 2 (0; 3; 0), A 3 (0; 0; 2).
Từ đó suy ra các khẳng định A và B là đúng.
Thể tích của khối tứ diện
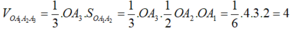
Vậy khẳng định C là đúng.
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho điểm . Gọi
A
1
,
A
2
,
A
3
lần lượt là hình chiếu vuông góc của A lên các trục Ox, Oy, Oz. Phương trình của mặt phẳng
A
1
A
2
A
3
là
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm . Gọi A 1 , A 2 , A 3 lần lượt là hình chiếu vuông góc của A lên các trục Ox, Oy, Oz. Phương trình của mặt phẳng A 1 A 2 A 3 là
![]()
![]()
![]()
![]()
Cho tam giác ABC nhọn và M là điểm tuỳ ý trong tam giác. A1, A2, A3 lần lượt là hình chiếu vuông góc của M trên cạnh BC, AC, AB. Tìm vị trí của M để MA1+MA2+MA3 đạt giá trị nhỏ nhất
điểm m là giao điểm của 3 đường phân giác
Đúng 0
Bình luận (0)
Dựa vào đồ thị vận tốc – thời gian của chất điểm được mô tả như hình bên. Gọi
a
1
;
a
2
và
a
3
lần lượt là gia tốc chuyển động của chất điểm trên đoạn OA; AB và BC. Giá trị
a
1
+
a
2
+
a
3
bằng A. 1m/s2. B. 2m/s2. C. 0m/s2. D....
Đọc tiếp
Dựa vào đồ thị vận tốc – thời gian của chất điểm được mô tả như hình bên. Gọi a 1 ; a 2 và a 3 lần lượt là gia tốc chuyển động của chất điểm trên đoạn OA; AB và BC. Giá trị a 1 + a 2 + a 3 bằng
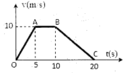
A. 1m/s2.
B. 2m/s2.
C. 0m/s2.
D. -1m/s2.
Chọn đáp án A
a 1 = 10 − 0 5 − 0 = 2 m / s 2 a 2 = 0 c h u y ể n đ ộ n g đ ề u a 3 = 0 − 10 20 − 10 = − 1 m / s 2 ⇒ a 1 + a 2 + a 3 = 1 m / s 2
Đúng 0
Bình luận (0)
Đồ thị vận tốc − thời gian của một vật chuyển động được biểu diễn như hình vẽ. Gọi
a
1
,
a
2
,
a
3
lần lượt là gia tốc của vật trong các giai đoạn tương ứng là từ t 0 đến
t
1
20
s
: từ
t
1
...
Đọc tiếp
Đồ thị vận tốc − thời gian của một vật chuyển động được biểu diễn như hình vẽ. Gọi a 1 , a 2 , a 3 lần lượt là gia tốc của vật trong các giai đoạn tương ứng là từ t = 0 đến t 1 = 20 s : từ t 1 = 20 s đến b = 60 s; từ t 2 = 60 s đến t 3 = 80 s . Giá trị của a 1 , a 2 , a 3 lần lượt là
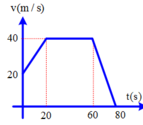
A. − 1 m / s 2 ; 0 ; 2 m / s 2
B. 1 m / s 2 ; 0 ; - 2 m / s 2
C. 1 m / s 2 ; 2 m / s 2 ; 0
D. 1 m / s 2 ; 0 ; 2 m / s 2
Cho hình chóp S.ABC có SA vuông góc với (ABC),
A
B
a
;
A
C
a
2
,
B
A
C
^
45
o
.
Gọi lần lượt là hình chiếu vuông góc của A lên SB, SC. Thể tích khối cầu ngoại tiếp hình chóp
A
....
Đọc tiếp
Cho hình chóp S.ABC có SA vuông góc với (ABC), A B = a ; A C = a 2 , B A C ^ = 45 o . Gọi lần lượt là hình chiếu vuông góc của A lên SB, SC. Thể tích khối cầu ngoại tiếp hình chóp A . B C C 1 B 1 bằng
A. π a 3 2 .
B. π a 3 2 .
C. 4 3 π a 3 .
D. π a 3 2 3 .
Cho hình chóp S.ABC có SA vuông góc với
A
B
C
,
A
B
a
;
C
A
a
2
;
B
A
C
45
°
. Gọi
B
1
;
C
1
lần lượt là hình chiếu vuông góc của A lên SB, SC...
Đọc tiếp
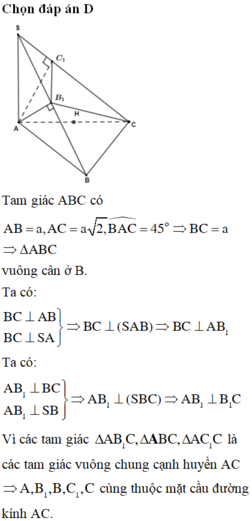
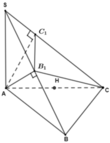
Cho hình chóp S.ABC có SA vuông góc với A B C , A B = a ; C A = a 2 ; B A C = 45 ° . Gọi B 1 ; C 1 lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích mặt cầu ngoại tiếp hình chóp A . B C C 1 B 1
A. V = π a 3 2 3
B. V = π a 3 2
C. V = 4 3 π a 3
D. V = π a 3 2
Đáp án A
Công thức
R = B C 2 sin B A C ⏜ = a 2 + 2 a 2 − 2 a . a 2 cos 45 ° 2 sin 45 ° = a 2 ⇒ V = 4 3 π R 3 = π a 3 2 3
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có SA vuông góc với (ABC),
A
B
a
;
A
C
a
2
;
B
A
C
^
45
o
.Gọi
B
1
;
C
1
lần lượt là hình chiếu vuông góc của A lên SB, SC. Thể tích khối cầu ngoại tiếp hình chóp...
Đọc tiếp
Cho hình chóp S.ABC có SA vuông góc với (ABC), A B = a ; A C = a 2 ; B A C ^ = 45 o .Gọi B 1 ; C 1 lần lượt là hình chiếu vuông góc của A lên SB, SC. Thể tích khối cầu ngoại tiếp hình chóp A . B C C 1 B 1 bằng
A. πa 3 2
B. πa 3 2
C. 4 3 πa 3
D. πa 3 2 3