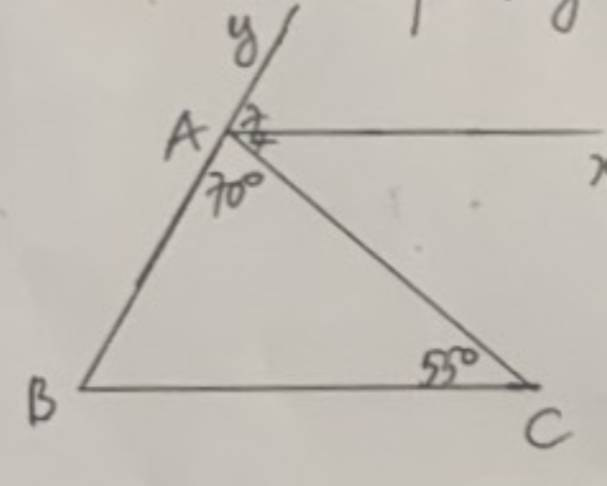
 chứng minh Ax//BC
chứng minh Ax//BC

Những câu hỏi liên quan
Cho tam giác ABC vuông tại C ,có AC <BC .vẽ tia phân giác Ax của góc Bac cắt BC tại I .qua B Vẽ đường thẳng vuông góc với Ax cắt tia Ax tại H
a, chứng minh tam giác AIC đồng dạng với tam giác BIH
b, cho AC=15cm,AC=25cm.Tính BC và CI
c, chứng minh HB^2=HI.HA
a) Xét tam giác AIC và tam giác BIH có:
\(\widehat{AIC}=\widehat{BIH}\)(đối đỉnh)
\(\widehat{ACI}=\widehat{BHI}=90^0\)
\(\Rightarrow\Delta AIC\sim\Delta BIH\left(g.g\right)\)
Câu b em xem lại đề nhé ! Sao AC=15cm và AC=25cm được nhỉ ?
Đúng 0
Bình luận (0)
Cho Δ ABC có B = C. Kẻ AH vuông góc với BC (H \(\in\) BC)
a) Chứng minh BAH = HAC
b) Kẻ Ax là tia phân giác của góc ngoài ở đỉnh A. Chứng minh Ax // BC
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là tia phân giác
hay \(\widehat{BAH}=\widehat{CAH}\)
b: \(\widehat{xAC}=\dfrac{180^0-\widehat{BAC}}{2}\)
\(\widehat{ACB}=\dfrac{180^0-\widehat{BAC}}{2}\)
Do đó: \(\widehat{xAC}=\widehat{ACB}\)
mà hai góc này ở vị trí so le trong
nên Ax//BC
Đúng 0
Bình luận (0)
tam giác ABC, kẻ Ax//BC (Ax và C nằm khác phía đối với AB. Trên Ax lấy M sao cho AM=BC. Chứng minh a; MB=AC b; MB=AC
Xét tứ giác AMBC có
AM//BC
AM=BC
Do đó: AMBC là hình bình hành
=>MB=AC
Đúng 1
Bình luận (0)
Vẽ tam góc ABC có AB bằng BC . Vẽ tia phân giác Ax của góa ngoài tại đỉnh A . Chứng minh rằng Ax // với BC
Cho tam giác ABC có AB =AC. Gọi M là trung điểm của BC. chứng minh : a) AM là đường trung trực của BC. b) kẽ đường phân giác Ax của góc ngoài A. chứng minh : Ax // BC
a) Xét △AMC và △AMB có:
AM chung
AC=AB (gt)
MC=MB (gt)
⇒ △AMC=△AMB (ccc)
\(\Rightarrow\widehat{AMC}=\widehat{AMB}=90^0\)
⇒AM⊥BC mà M là trung điểm của BC nên AM là đường trung trực của BC (đpcm)
b)Gọi \(\widehat{BAy}\) là góc ngoài tại đỉnh A của △ABC
Ta có:
\(\widehat{BAy}=180^0-\widehat{BAC}\)
\(\Rightarrow\frac{1}{2}\widehat{BAy}=\frac{180^0-\widehat{BAC}}{2}\)
\(\Rightarrow\widehat{BAx}=\widehat{ABC}\) mà 2 góc này ở vị trí so le trong nên Ax//BC (đpcm)
cho ΔABCt ừ A vẽ tia Ax // BC trên Ax lấy M sao cho AM=BC
chứng minh MC=AB
Bạn tự vẽ hình nha
Ax // BC
=> CAM = ACB (2 góc so le trong)
Xét tam giác ACB và tam giác CAM có:
AC là cạnh chung
ACB = CAM (chứng minh trên)
CB = AM (gt)
=> Tam giác ACB = Tam giác CAM (c.g.c)
=> AB = CM (2 cạnh tương ứng)
Chúc bạn học tốt ^^
Đúng 0
Bình luận (0)
xét tam giác ABC và AMC :
AM = BC (gt)
Ax // BC => góc MAC = góc ACB slt
AC là cạnh chung
vậy tam giác AMC = tam giác ABC (c.g.c)
=> AB // MC
Đúng 0
Bình luận (0)
Câu 13: (2 điểm) Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC. a) Chứng minh: ABM = ACM. b) Gọi Ay là tia đối của tia AB và Ax là tia phân giác góc ngoài ở đỉnh A. Chứng minh: Ax // BC.
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
Đúng 1
Bình luận (1)
Câu 13: (2 điểm) Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC. a) Chứng minh: ABM = ACM. b) Gọi Ay là tia đối của tia AB và Ax là tia phân giác góc ngoài ở đỉnh A. Chứng minh: Ax // BC.
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
Đúng 0
Bình luận (0)
1. Cho đường tròn (O), đường kính AB, dây AM. Kéo dài AM một đoạn MC AMa) Chứng minh AB BCb) Gọi N là trung điểm BC. Chứng minh tứ giác BOMN là hình thoi.2. Cho đường tròn (O), đường kính AB, tiếp tuyến Ax. Trên Ax lấy điểm M, vẽ tiếp tuyếnMC với đường tròn (C là tiếp điểm).a) Chứng minh OM // BCb) Từ O vẽ đường thẳng vuông góc AB cắt BC tại N. Chứng minh BOMN là hình bình hànhc) Chứng minh COMN là hình thang cân3.Cho đường tròn (O), đường kính AB, tiếp tuyến Ax. Trên Ax lấy điểm M, vẽ tiếp tu...
Đọc tiếp
1. Cho đường tròn (O), đường kính AB, dây AM. Kéo dài AM một đoạn MC = AM
a) Chứng minh AB = BC
b) Gọi N là trung điểm BC. Chứng minh tứ giác BOMN là hình thoi.
2. Cho đường tròn (O), đường kính AB, tiếp tuyến Ax. Trên Ax lấy điểm M, vẽ tiếp tuyến
MC với đường tròn (C là tiếp điểm).
a) Chứng minh OM // BC
b) Từ O vẽ đường thẳng vuông góc AB cắt BC tại N. Chứng minh BOMN là hình bình hành
c) Chứng minh COMN là hình thang cân
3.Cho đường tròn (O), đường kính AB, tiếp tuyến Ax. Trên Ax lấy điểm M, vẽ tiếp tuyến
MC với đường tròn (C là tiếp điểm).Kẻ CH vuông góc với AB tại H
a) Chứng minh CA là phân giác góc HCM
b) Kẻ CH vuông góc Ax tại K, gọi I là giao điểm của AC và HK. Chứng minh tam giác AIO vuông
c) Chứng minh 3 điểm M, I, O thẳng hàng
















