Tìm tất cả giá trị của m để khoảng cách từ gốc tọa độ đến (d):y=(m-2)x + 3 bằng 1

Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
-
3
m
x
2
+
3
(
m
2
-
1
)
x
-...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + 3 ( m 2 - 1 ) x - m 3 + m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O
A. m = - 3 - 2 2 h o ặ c m = - 1
B. m = - 3 + 2 2 h o ặ c m = - 1
C. m = - 3 + 2 2 h o ặ c m = - 3 - 2 2 .
D. m = - 3 + 2 2
Chọn C
Ta có y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 )
Hàm số (1) có cực trị thì PT y ' = 0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nhiệm phân biệt
![]()
Khi đó, điểm cực đại A ( m - 1 ; 2 - 2 m ) và điểm cực tiểu B ( m + 1 ; - 2 m )
Ta có O A = 2 O B ⇔ m 2 + 6 m + 1 = 0
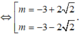
Đúng 0
Bình luận (0)
Giúp mình với ạ
cho hàm số: y=(m-2)x+m-1
với m≠1, Tìm tất cả giá trụ của m để khoảng cách từ gốc tọa độ đến (d) bằng 2(đvđd)
Sửa đề: \(m\ne2\)
\(y=\left(m-2\right)x+m-1\)
=>\(\left(m-2\right)x-y+m-1=0\)
Khoảng cách từ O(0;0) đến (d) là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot\left(m-2\right)+0\cdot\left(-1\right)+m-1\right|}{\sqrt{\left(m-2\right)^2+\left(-1\right)^2}}\)
\(=\dfrac{\left|m-1\right|}{\sqrt{\left(m-2\right)^2+1}}\)
Để \(d\left(O;\left(d\right)\right)=2\) thì \(\dfrac{\left|m-1\right|}{\sqrt{\left(m-2\right)^2+1}}=2\)
=>\(\left|m-1\right|=\sqrt{4\left(m-2\right)^2+4}\)
=>\(\sqrt{4\left(m-2\right)^2+4}=\sqrt{\left(m-1\right)^2}\)
=>\(4\left(m-2\right)^2+4=\left(m-1\right)^2\)
=>\(4\left(m^2-4m+4\right)+4-m^2+2m-1=0\)
=>\(4m^2-16m+16-m^2+2m+3=0\)
=>\(3m^2-14m+19=0\)(1)
\(\text{Δ}=\left(-14\right)^2-4\cdot3\cdot19\)
\(=196-12\cdot19=-32< 0\)
=>Phương trình (1) vô nghiệm
Vậy: \(m\in\varnothing\)
Đúng 2
Bình luận (0)
Cho đường thẳng: y=(m-2)x +2 (d) a, Chứng minh rằng đường thẳng d luôn đi qua một điểm cố định với mọi giá trị của m b, Tìm giá trị của m để khoảng cách từ gốc tọa độ đến đường thẳng d bằng 1 c, Tìm giá trị của m để khoảng cách từ gốc tọa độ đến đường thẳng d có giá trị lớn nhất
Cho đường thẳng y = (m - 2)x +2 (d)
a) Chứng minh rằng đường thẳng d luôn đi qua một điểm cố định với mọi giá trị của m
b) Tìm giá trị của m để khoảng cách từ gốc tọa độ đến đường thẳng d bằng 1
c) Tìm giá trị của m để khoảng cách từ gốc tọa độ đến đường thẳng d có giá trị lớn nhất
Tính tổng tất cả các giá trị thực của tham số m để hàm số y x3-3mx2+ 3( m2-1) x- m3+ m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng
2
lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O. A. -4 B. -5 C. -6. D. -7
Đọc tiếp
Tính tổng tất cả các giá trị thực của tham số m để hàm số y= x3-3mx2+ 3( m2-1) x- m3+ m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O.
A. -4
B. -5
C. -6.
D. -7
Ta có y’ = 3x2- 6mx + 3( m2-1).
Hàm số đã cho có cực trị thì phương trình y’ =0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nghiệm phân biệt ⇔ ∆ = 1 > 0 , ∀ m
Khi đó, điểm cực đại A( m-1; 2-2m) và điểm cực tiểu B( m+1; -2-2m)
Ta có
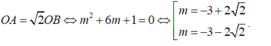
Tổng hai giá trị này là -6.
Chọn C.
Đúng 0
Bình luận (0)
cho đường thẳng (d): y=m(2x-1)+3-2x
a) Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng (d) bằng 1.
a) Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng (d) đạt giá trị lớn nhất.
cho đường thẳng y=(m-2) x+2 (d) a, CMR: đường thẳng (d) luôn đi qua 1 điểm cố định với mọi m b,tìm già trị của m để khoảng cách từ gốc tọa độ đến đương thẳng (d) =1 c, tìm giá trị của m để khoảng cách từ gốc tọa độ đến đường thẳng m là lớn nhất
\(a,\) Gọi điểm cố định (d) luôn đi qua là \(A\left(x_0;y_0\right)\)
\(\Leftrightarrow y_0=\left(m-2\right)x_0+2\Leftrightarrow mx_0-2x_0+2-y_0=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0=0\\2-2x_0-y_0=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=0\\y_0=2\end{matrix}\right.\Leftrightarrow A\left(0;2\right)\)
Vậy \(A\left(0;2\right)\) là điểm cố định mà (d) lun đi qua
\(b,\) PT giao Ox,Oy: \(y=0\Leftrightarrow x=\dfrac{2}{2-m}\Leftrightarrow B\left(\dfrac{2}{2-m};0\right)\Leftrightarrow OB=\dfrac{2}{\left|m-2\right|}\\ x=0\Leftrightarrow y=2\Leftrightarrow C\left(0;2\right)\Leftrightarrow OC=2\)
Gọi H là chân đường cao từ O đến (d) \(\Leftrightarrow OH=1\)
Áp dụng HTL: \(\dfrac{1}{OH^2}=1=\dfrac{1}{OB^2}+\dfrac{1}{OC^2}=\dfrac{\left(m-2\right)^2}{4}+\dfrac{1}{4}\)
\(\Leftrightarrow m^2-4m+4+1=4\\ \Leftrightarrow m^2-4m+1=0\\ \Leftrightarrow\left[{}\begin{matrix}m=2+\sqrt{3}\\m=2-\sqrt{3}\end{matrix}\right.\)
\(c,\) Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OC^2}+\dfrac{1}{OB^2}=\dfrac{\left(m-2\right)^2}{4}+\dfrac{1}{4}\)
Đặt \(OH^2=t\)
\(\Leftrightarrow\dfrac{1}{t}=\dfrac{m^2-4m+5}{4}\Leftrightarrow t=\dfrac{4}{\left(m-2\right)^2+1}\le\dfrac{4}{0+1}=4\\ \Leftrightarrow OH\le2\\ OH_{max}=2\Leftrightarrow m=2\)
Đúng 1
Bình luận (0)
Cho đường thẳng: y(m-2)x +2 (d)a, Chứng minh rằng đường thẳng d luôn đi qua một điểm cố định với mọi giá trị của mb, Tìm giá trị của m để khoảng cách từ gốc tọa độ đến đường thẳng d bằng 1c, Tìm giá trị của m để khoảng cách từ gốc tọa độ đến đường thẳng d có giá trị lớn nhất
Đọc tiếp
Cho đường thẳng: y=(m-2)x +2 (d)
a, Chứng minh rằng đường thẳng d luôn đi qua một điểm cố định với mọi giá trị của m
b, Tìm giá trị của m để khoảng cách từ gốc tọa độ đến đường thẳng d bằng 1
c, Tìm giá trị của m để khoảng cách từ gốc tọa độ đến đường thẳng d có giá trị lớn nhất
Cho đường thẳng: y(m-2)x +2 (d)a, Chứng minh rằng đường thẳng d luôn đi qua một điểm cố định với mọi giá trị của mb, Tìm giá trị của m để khoảng cách từ gốc tọa độ đến đường thẳng d bằng 1c, Tìm giá trị của m để khoảng cách từ gốc tọa độ đến đường thẳng d có giá trị lớn nhất
Đọc tiếp
Cho đường thẳng: y=(m-2)x +2 (d)
a, Chứng minh rằng đường thẳng d luôn đi qua một điểm cố định với mọi giá trị của m
b, Tìm giá trị của m để khoảng cách từ gốc tọa độ đến đường thẳng d bằng 1
c, Tìm giá trị của m để khoảng cách từ gốc tọa độ đến đường thẳng d có giá trị lớn nhất













