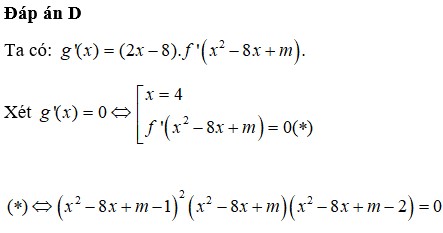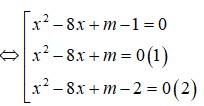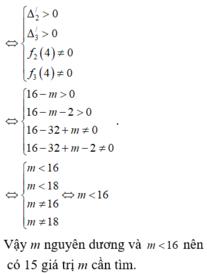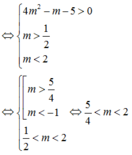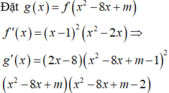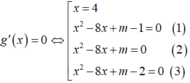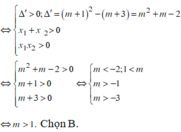cho y=f(x)= x^3 -2x^2+(2-m)x+1 tìm m để hs y=f(|x|) có 5 đ cực trị

Những câu hỏi liên quan
Cho hàm số yf(x) có đạo hàm f’(x)(x-1)2(x2-2x) với mọi
x
∈
R
. Có bao nhiêu giá trị nguyên dương của tham số m để hàm yf(x2-8x+m) có 5 điểm cực trị A. 15 B. 17 C. 18 D. 16
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f’(x)=(x-1)2(x2-2x) với mọi x ∈ R . Có bao nhiêu giá trị nguyên dương của tham số m để hàm y=f(x2-8x+m) có 5 điểm cực trị
A. 15
B. 17
C. 18
D. 16
a) f(x)= -1/3x^3 + x^2 -2x +10 tìm điểm cực trị của hs
b) tìm m để hs y=x^3 +3mx^2 + 3(m^2 - 1 )x + m^2 - 3m đạt CĐ,CT tại x1,x2 sao cho x1^2 + x2^2 = 10
Cho hàm số yf(x) có đạo hàm
f
(
x
)
(
x
-
1
)
2
(
x
2
-
2
x
)
, với mọi
x
∈
R
. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = ( x - 1 ) 2 ( x 2 - 2 x ) , với mọi x ∈ R . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f ( x 2 - 8 x + m ) có 5 điểm cực trị?
A. 16
B. 18
C. 17
D. 15
Cho hàm số yf(x) có đạo hàm
f
(
x
)
(
x
-
1
)
2
(
x
2
-
2
x
)
với mọi x thuộc R. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số
y
f
(
x
2
-...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = ( x - 1 ) 2 ( x 2 - 2 x ) với mọi x thuộc R. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f ( x 2 - 8 x + m ) có 5 điểm cực trị?
A. 15
B. 17
C. 16.
D. 18
1.y=\(\dfrac{1}{3}x^3-2mx^2+3x+1\) tìm m để hs có cực đại, cực tiểu
2. y=\(x^3-mx^2+\left(m^2-6\right)x+1\) tìm m để hs đạt cực trị tại x=1, khi đó hs là điểm cực đại hay cực tiểu
Cho HS y = x^3 - (2m-1).x^2 + (2-m).x +2. Tìm m để HS có cực đại, cực tiểu và các điểm cực trị của HS có hoành độ dương.
\(y'=3x^2-2\left(2m-1\right)x+2-m\)
Hàm có các cực trị dương khi pt \(y'=0\) có 2 nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=\left(2m-1\right)^2-3\left(2-m\right)>0\\x_1+x_2=\dfrac{2\left(2m-1\right)}{3}>0\\x_1x_2=\dfrac{2-m}{3}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4m^2-m-5>0\\m>\dfrac{1}{2}\\m< 2\end{matrix}\right.\) \(\Rightarrow\dfrac{5}{4}< m< 2\)
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
x
3
–
(
2
m
-
1
)
x
2
+
(
2
-
m
)
x
+
2
. Tìm tất cả các giá trị thực của tham số m để hàm số yf(|x|) có 5 cực trị A.
-
10
m
5
4
B.
-...
Đọc tiếp
Cho hàm số f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tìm tất cả các giá trị thực của tham số m để hàm số y=f(|x|) có 5 cực trị
A. - 10 < m < 5 4
B. - 2 < m < 5
C. - 2 < m < 5 4
D. 5 4 < m < 2
Cho hàm số yf(x) có đạo hàm f(x)
(
x
-
1
)
2
(
x
2
-
2
x
)...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f'(x) = ( x - 1 ) 2 ( x 2 - 2 x ) với ∀ x ∈ ℝ . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số có 5 điểm cực trị?
A. 15
B. 17
C. 16
D. 18
Cho hàm số
y
1
3
x
3
-
(
m
+
1
)
x
2
+
(
m
+
3
)
x
+
m
-
4
. Tìm m để hàm số yf(|x|) có 5 điểm cực trị A. -3m-1 B. m1 C. m4 D. m0
Đọc tiếp
Cho hàm số y = 1 3 x 3 - ( m + 1 ) x 2 + ( m + 3 ) x + m - 4 . Tìm m để hàm số y=f(|x|) có 5 điểm cực trị
A. -3<m<-1
B. m>1
C. m>4
D. m>0