Dạ mọi người giúp em câu này với ạ
Dạ mọi người giúp em câu này với ạ

a)\(\left\{{}\begin{matrix}\xi_b=\xi_1+\xi_2=6+3=9V\\r_b=r_1+r_2=2+1=3\Omega\end{matrix}\right.\)
b)CTM ngoài: \(R_1nt\left(R_2//R_3\right)\)
\(R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{2\cdot8}{2+8}=1,6\Omega\)
\(R_N=R_1+R_{23}=4,4+1,6=6\Omega\)
c)\(I_1=I_{23}=I=\dfrac{\xi_b}{r_b+R_N}=\dfrac{9}{3+6}=1A\)
\(U_1=I_1\cdot R_1=1\cdot4,4=4,4V\)
\(U_2=U_3=U_{23}=I_{23}\cdot R_{23}=1\cdot1,6=1,6V\)
Dạ mọi người chỉ em gấp bài này với ạ. Dạ mọi người chỉ ra dẫn chứng giúp em luôn với ạ




Dạ mọi người chỉ em gấp bài này với ạ. Dạ mọi người chỉ ra dẫn chứng giúp em luôn với ạ



Dạ mọi người chỉ em bài này với ạ. Dạ mọi người ghi rõ đáp án cần sửa là gì luôn giúp em với ạ


35 A => on the flip side
36 A => in
37 C => have been derived
38 D => tremediously
39 B => becomes
40 D => of which
41 C => minority languages
42 C => lie under
43 B => happens
44 B => percent
45 C => have been born
46 B=> of whom
47 C => as well as
48 A bỏ đi
49 C => ethnicity
50 C => sacrificing
Dạ mọi người giúp em bài 4 câu b với ạ Dạ em cảm ơn ạ
\(a^3+b^3=\sqrt{\left(\sqrt{6}-\sqrt{2}\right)^2}-\dfrac{4\left(\sqrt{6}-\sqrt{2}\right)}{\left(\sqrt{6}+\sqrt{2}\right)\left(\sqrt{6}-\sqrt{2}\right)}\)
\(=\sqrt{6}-\sqrt{2}-\dfrac{4\left(\sqrt{6}-\sqrt{2}\right)}{4}=0\)
\(\Rightarrow a=-b\Rightarrow a^5+b^5=0\)
Giúp em 2 bài này với ạ, dạ em ghi nhầm x thành n ạ mọi người giúp với bỏ qua cho em
3) \(\sqrt{\left(x-2\right)\left(x+1\right)}\) thì (x-2)(x+1)>0
=> x2 -x-2>0
=> x2 - x - \(\dfrac{1}{2}\)- \(\dfrac{3}{2}\)>0
= (x+\(\dfrac{1}{4}\))2 - 3/2 >0
=> x+ 1/4>3/2
=> x>5/4
4) Có x đâu mà tìm bạn??
4) \(\sqrt{x^2+2x+1}\) + \(\sqrt{x^2-2x+1}\)= \(\sqrt{\left(x+1\right)^2}\) + \(\sqrt{\left(x-1\right)^2}\)
=> /x+1/+/x-1/ = 2
=> /2x/ = 2
=> 2x=2
=> x=1
Để biểu thức có nghĩa thì (x-2)(x+1)>0
\(\Leftrightarrow\left[{}\begin{matrix}x>2\\x< -1\end{matrix}\right.\)
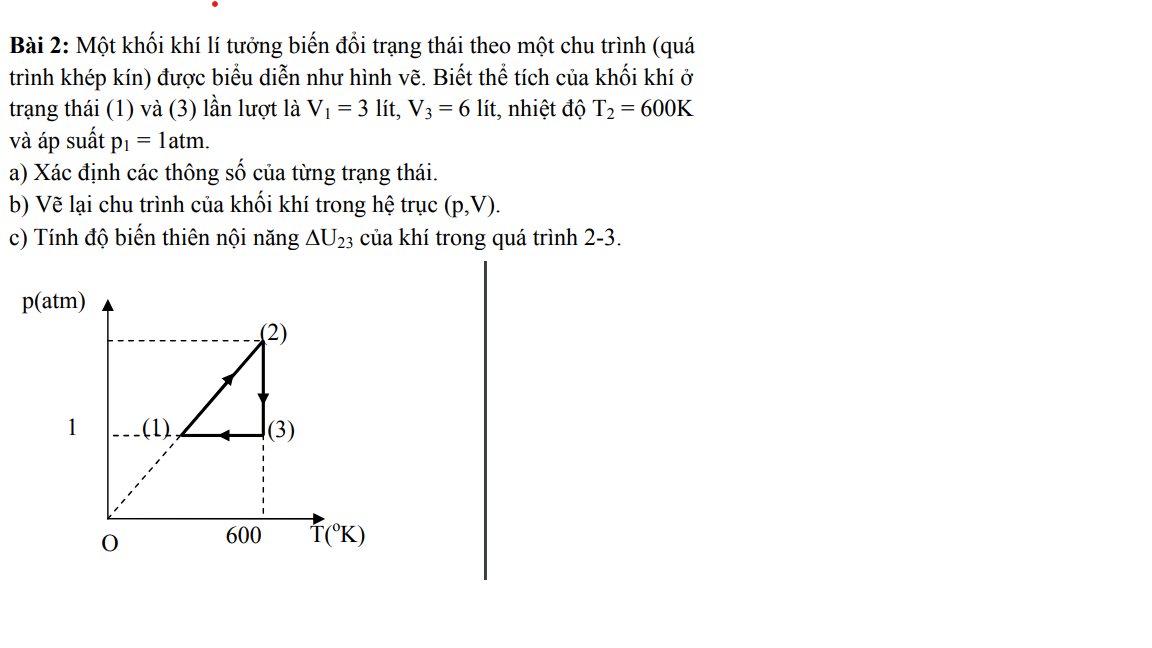
Dạ em chỉ cần câu c thôi ạ, mọi người giúp em với ạ
Dạ mọi người giúp em câu 3 với ạ

Dạ mọi người giúp em 3 câu 4,5,6 gấp với ạ

Để tính quãng đường đi được từ thời điểm t1 đến t2 cho vật giao động điều hòa dọc theo trục Ox, ta cần tính diện tích dưới đường cong x(t) trong khoảng thời gian từ t1 đến t2.
Trước tiên, chúng ta sẽ tính x(t) tại t1 và t2:
Tại t1 = 13/6 s: x(t1) = 3 * cos(4 * 3.14 - (3.14 / 3)) cm
Tại t2 = 23/6 s: x(t2) = 3 * cos(4 * 3.14 - (3.14 / 3)) cm
Tiếp theo, chúng ta cần tính diện tích dưới đường cong trong khoảng từ t1 đến t2. Để làm điều này, ta sẽ tính diện tích của hình giữa đồ thị và trục Ox trong khoảng từ t1 đến t2.
Diện tích A = ∫(t1 đến t2) x(t) dt
A = ∫(13/6 đến 23/6) [3 * cos(4 * 3.14 - (3.14 / 3))] dt
A = ∫(13/6 đến 23/6) [3 * cos(4 * 3.14 - 3.14/3)] dt
A = ∫(13/6 đến 23/6) [3 * cos(4 * 3.14 - 3.14/3)] dt
A = ∫(13/6 đến 23/6) [3 * cos(12.56 - 1.0467)] dt
A = ∫(13/6 đến 23/6) [3 * cos(11.5133)] dt
Giải tích phần này trở nên phức tạp, nhưng bạn có thể tính toán nó bằng máy tính hoặc phần mềm tính toán. Kết quả sẽ là diện tích A, tức là quãng đường đi được từ t1 đến t2.
(em thay pi=3,14 luôn nha anh )
em gúp anh đc câu 6 chứ mấy câu kia lười quá;-;