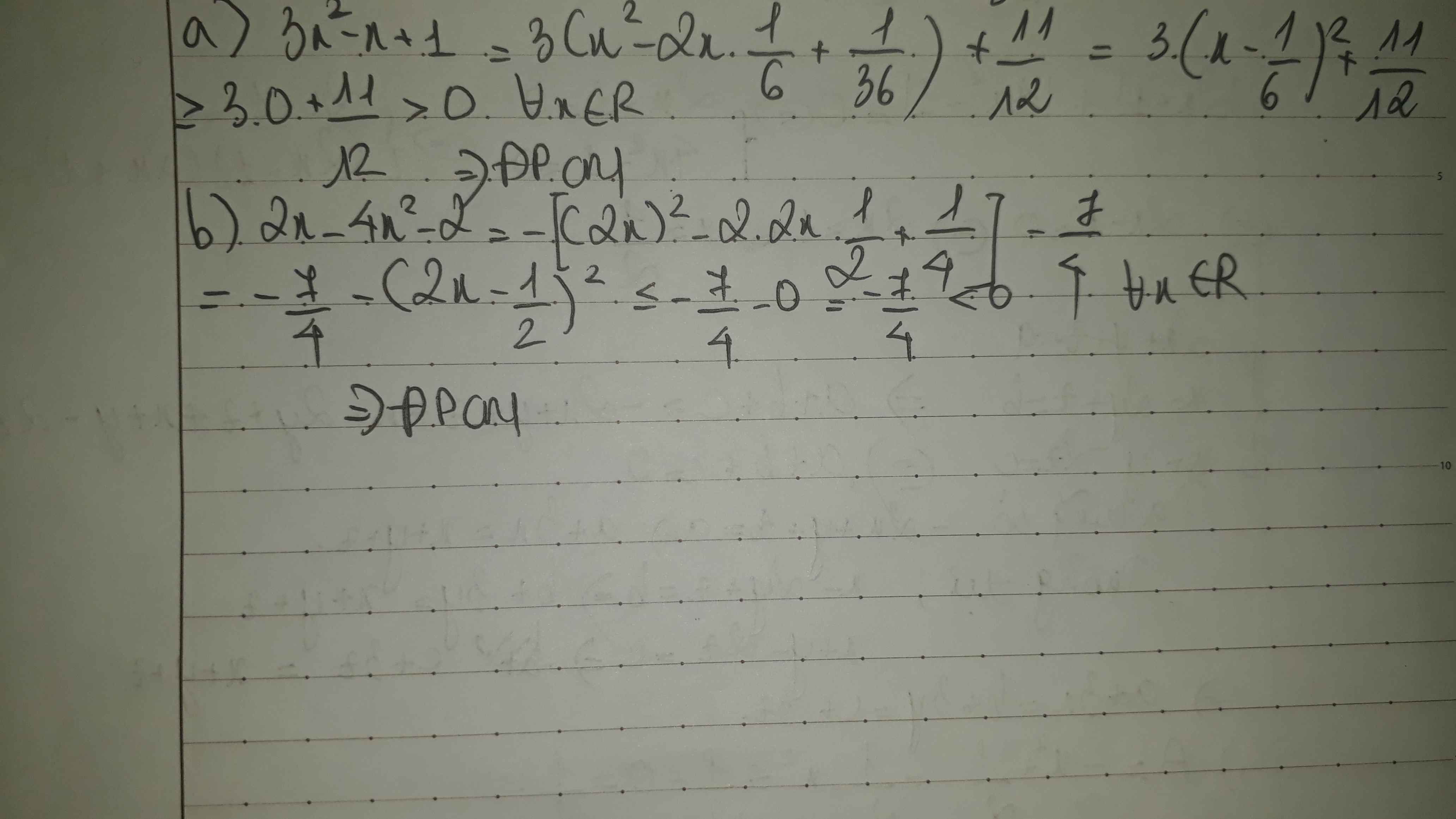\(-4x^2+4x-12< 0 \)
\(\Leftrightarrow-\left(4x^2-4x+1\right)-11< 0\)
\(\Leftrightarrow-\left(2x-1\right)^2-11< 0\left(đpcm\right)\)

Ta có:   \(-4x^2+4x-12=-\left(2x\right)^2+4x-1-11\)=\(\left[-\left(2x\right)^2+4x-1\right]-11\)

             \(=-\left(2x-1\right)^2-11\)

Vì \(\left(2x-1^2\right)>0\)\(\forall x\)

\(-\left(2x-1\right)^2< 0\)\(\forall x\)

\(-\left(2x-1\right)^2-11< -11< 0\)\(\forall x\)

hay \(-4x^2+4x-12< 0\)\(\forall x\)

a) Xét \(x^2-4x+4=\left(x-2\right)^2\ge0\)

<=> \(x^2-4x\ge-4>-5\)

b) \(2x^2+4y^2-4x-4xy+5\)

= \(\left(x^2-4x+4\right)+\left(x^2-4xy+4y^2\right)+1\)

= \(\left(x-2\right)^2+\left(x-2y\right)^2+1\ge1>0\)

Câu a :

\(x^2+x+1=x^2+x+\dfrac{1}{4}+\dfrac{3}{4}=\left(x+\dfrac{1}{2}\right)^2\ge\dfrac{3}{4}\)

Vậy biểu thức trên luôn lớn hơn 0 với mọi x

Làm Full cho you nhé,bạn kia sai r:

\(linh_1=x^2+x+1=x^2+x+\dfrac{1}{4}+\dfrac{3}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\left(đpcm\right)\)

\(linh_2=-4x^2-4x-2=-1\left(4x^2+4x+2\right)=-1\left(4x^2+4x+1+1\right)=-1\left(4x^2+4x+1\right)-1=-1\left(2x+1\right)^2-1< 0\left(đpcm\right)\)

1) \(A=x^2+2x+2=\left(x+1\right)^2+1\ge1>0\left(\forall x\right)\)

2) \(B=x^2+6x+11=\left(x+3\right)^2+2\ge2>0\left(\forall x\right)\)

3) \(C=4x^2+4x-2=\left(2x+1\right)^2-2\ge-2\) chưa chắc nhỏ hơn 0

4) \(D=-x^2-6x-11=-\left(x+3\right)^2-2\le-2< 0\left(\forall x\right)\)

5) \(E=-4x^2+4x-2=-\left(2x-1\right)^2-1\le-1< 0\left(\forall x\right)\)

1. \(A=x^2+2x+2=\left(x+1\right)^2+1\)

Vì \(\left(x+1\right)^2\ge0\forall x\)\(\Rightarrow\left(x+1\right)^2+1\ge1\)

=> Đpcm

2. \(B=x^2+6x+11=\left(x+3\right)^2+2\)

Vì \(\left(x+3\right)^2\ge0\forall x\)\(\Rightarrow\left(x+3\right)^2+2\ge2\)

=> Đpcm

3. \(C=4x^2+4x-2=-\left(4x^2-4x+2\right)\)

\(=-\left(4\left(x-\frac{1}{2}\right)^2+1\right)\)

Vì \(\left(x-\frac{1}{2}\right)^2\ge0\forall x\Rightarrow4\left(x-\frac{1}{2}\right)^2+1\ge1\)

\(\Rightarrow-\left(4\left(x-\frac{1}{2}\right)^2+1\right)\le1\)

=> Đpcm

4,5 làm tương tự

\(1.A=x^2+2x+2=\left(x+1\right)^2+1\)

Vì\(\left(x+1\right)^2\ge0\forall x\)

\(\Rightarrow\left(x+1\right)^2+1\ge1\forall x\)

hay\(\left(x+1\right)^2+1>0\forall x\)

\(2.B=x^2+2x.3+9+2=\left(x+3\right)^2+2\)

CM tương tự A

\(3.C=4x^2+4x-2=\left(2x+1\right)^2-2\)

Vì\(\left(2x+1\right)^2\ge0\forall x\)

\(\Rightarrow\left(2x+1\right)^2-2\ge-2\forall x\)(có thể >0)

4,5 Cm tương tự

Ta có : x² + 2x + 2

= x² + 2x + 1 + 1

= (x + 1)² + 1 \(\ge1\forall x\)

Vậy  x² + 2x + 2 \(>0\forall x\)

Ta có : x² + 2x + 2

=> x² + 2x + 1 + 1

=> ( x + 1)² + 1  >  1\(\forall x\)

Vậy x² + 2x + 2   > \(0\forall x\)

x^2 + 2x + 2 = x^2 + 2.x.1 + 1^2 +1 = (x + 1)^2 + 1 > 0

-x^2 + 4x - 4 = -(x^2 - 2.x.2 + 2^2) = -(x - 2)^2 <= 0

a) ta co ; x^2+ 2x+ 2= (x²+2x+1)+1=(x+1)²+1>0

vi (x+1)²>hoặc=0;1>0suy ra x^2+ 2x+ 2>0

b)ta co  -x²+4x-4=-(x²-4x+4)=-(x-2)²<0

a) x^2 + 2x + 2 = ( x^2 + 2x +1 ) + 1 =( x + 1)^2 +1 >0 với mọi x 

b) -x^2 + 4x - 4 = -( x^2 -4x + 4 ) = - ( x - 2)^2  ≤ 0 với mọi x

\(4x-x^2-5=-\left(x^2-4x+4\right)-1=-\left(x-2\right)^2-1\le-1< 0\)

câu a hình như bạn ghi sai đề rồi

câu b:

Ta có: \(x^2-4x+12=x^2-4x+4+8\)

\(=\left(x-2\right)^2+8\)

Ta có: \(\left(x-2\right)^2\ge0\forall x\in Q\)

\(\Rightarrow\text{​​}\left(x-2\right)^2+8\ge8>0\forall x\in Q\)

Do đó: \(x^2-4x+12>0\forall x\in Q\)(đpcm)