Cho 2 số a, b thỏa mãn a + b =2. Tìm giá trị nhỏ nhất của biểu thức M =a^4 + b^4+6a^2b^2

Những câu hỏi liên quan
Bài 6:Cho các số a,b,c khác 0 thỏa mãn
2a-2b+9c=9 Tính giá trị của M=a+3c/a+4b-3c
a-2b+6c=5
Bài 7 Cho a,b>0 thỏa mãn a+b=3.Tìm giá trị nhỏ nhất của biểu thức T=a^2+4/a+b^2/b+3
Bài 6:Cho các số a,b,c khác 0 thỏa mãn
2a-2b+9c=9 Tính giá trị của M=a+3c/a+4b-3c
a-2b+6c=5
Bài 7 Cho a,b>0 thỏa mãn a+b=3.Tìm giá trị nhỏ nhất của biểu thức T=a^2+4/a+b^2/b+3
câu1:
a) Cho các số thực không âm a, b, c thỏa mãn a + b + c =1. Tìm giá trị lớn nhất và giá trị nhỏ
nhất của biểu thức:
P=\(\frac{ab+bc+ca-abc}{a+2b+c}\)
b) Cho các số thực a, b, c thỏa mãn \(^{a^2+b^2+c^2=1}\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P =ab +bc + ca .
Cho hai số thực a,b thỏa mãn
a
0,0
b
2
. Tìm giá trị nhỏ nhất của biểu thức
P
(
2
b
)
a
2
a
−
b
a...
Đọc tiếp
Cho hai số thực a,b thỏa mãn a > 0,0 < b < 2 . Tìm giá trị nhỏ nhất của biểu thức P = ( 2 b ) a 2 a − b a 2 + 2 a + 2 b a 2 b a
A. P min = 9 4 .
B. P min = 7 4 .
C. P min = 13 4 .
D. P min = 4.
Đáp án C.
Ta có P = 2 b a 2 b a − 1 2 + 1 2 . 2 b a + 1. Đặt t = 2 b a , do 0 < b < 2 → t > 1.
Xét hàm số f ( t ) = t t − 1 2 + t 2 + 1 trên 1 ; + ∞ .
Đạo hàm
f ' ( t ) = ( t − 1 ) 2 − 2 t ( t − 1 ) ( t − 1 ) 4 + 1 2 = t + 1 ( t − 1 ) 3 + 1 2 ; f ' ( t ) = 0 ⇔ t = 3.
Lập bảng biến thiên của hàm số, ta thấy min f ( x ) = f ( 3 ) = 13 4 . Vậy P min = 13 4 .
Đúng 0
Bình luận (0)
Cho a , b là hai số thực dương thỏa mãn
log
5
4
a
+
2
b
+
5
a
+
b
a
+
3
b
-
4
. Tìm giá trị nhỏ nhất của biểu thức
T...
Đọc tiếp
Cho a , b là hai số thực dương thỏa mãn log 5 4 a + 2 b + 5 a + b = a + 3 b - 4 . Tìm giá trị nhỏ nhất của biểu thức T = a 2 + b 2
A. 1 2
B. 1.
C. 3 2
D. 5 2
Ta có:
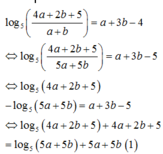
Xét hàm số
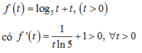
Hàm số f t đồng biến trên 0 ; + ∞
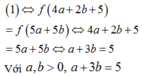
ta có:
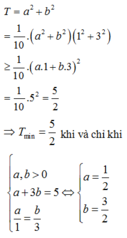
Chọn: D
Đúng 0
Bình luận (0)
Cho a;b là hai số thực dương thỏa mãn
log
5
4
a
+
2
b
+
5
a
+
b
a
+
3
b
−
4
. Tìm giá trị nhỏ nhất của biểu thức
T...
Đọc tiếp
Cho a;b là hai số thực dương thỏa mãn log 5 4 a + 2 b + 5 a + b = a + 3 b − 4 . Tìm giá trị nhỏ nhất của biểu thức T = a 2 + b 2
A. 1/2
B. 5/2
C. 3/2
D. 1
Đáp án B
Ta có: log 5 4 a + 2 b + 5 a + b = a + 3 b − 4
⇔ log 5 4 a + 2 b + 5 + 4 a + 2 b + 5 = log 5 5 a + 5 b + 5 a + 5 b
Xét hàm số f t = log 5 t + t t > 0 ⇒ f t đồng biến trên 0 ; + ∞
Do đó f 4 a + 2 b + 5 = f 5 a + 5 b ⇔ 4 a + 2 b + 5 = 5 a + 5 b
⇔ a + 3 b = 5 ⇒ T = 5 − 3 b 2 + b 2 = 10 b 2 − 30 b + 25 = 10 b − 3 2 2 + 5 2 ≥ 5 2
Đúng 0
Bình luận (0)
Cho hai số thực dương a, b thỏa mãn \(a+2b\ge3\). Tìm giá trị nhỏ nhất của biểu thức \(P=\dfrac{3a^2+a^2b+\dfrac{9}{2}ab^2+\left(8+a\right)b^3}{ab}\)
1. Cho số nguyên dương x, tìm giá trị nhỏ nhất của biểu thức:Pdfrac{left(x+1right)^6}{left(x^3+7right)left(x^3+3x^2+4right)}. 2. Cho a,bge0 thỏa mãn a-sqrt{a}sqrt{b}-b, tìm giá trị nhỏ nhất của biểu thức:Mleft(a-bright)left(a+b-1right). 3. Cho Delta OEF vuông tại O có OEa, OFb, EFc và widehat{OEF}alpha, widehat{OFE}beta.1)i, Chứng minh rằng không có giá trị nào của a,b,c để biểu thức Adfrac{a+b}{c}+dfrac{c}{a+b} nhận giá trị nguyên.ii, Giả sử csqrt{ab}sqrt{2} , tìm giá trị nhỏ nhất của biểu thức...
Đọc tiếp
1. Cho số nguyên dương x, tìm giá trị nhỏ nhất của biểu thức:
\(P=\dfrac{\left(x+1\right)^6}{\left(x^3+7\right)\left(x^3+3x^2+4\right)}\).
2. Cho \(a,b\ge0\) thỏa mãn \(a-\sqrt{a}=\sqrt{b}-b\), tìm giá trị nhỏ nhất của biểu thức:
\(M=\left(a-b\right)\left(a+b-1\right)\).
3. Cho \(\Delta OEF\) vuông tại O có \(OE=a\), \(OF=b\), \(EF=c\) và \(\widehat{OEF}=\alpha\), \(\widehat{OFE}=\beta\).
1)
i, Chứng minh rằng không có giá trị nào của a,b,c để biểu thức \(A=\dfrac{a+b}{c}+\dfrac{c}{a+b}\) nhận giá trị nguyên.
ii, Giả sử \(c\sqrt{ab}=\sqrt{2}\) , tìm giá trị nhỏ nhất của biểu thức \(B=\left(a+b\right)^2\).
2)
i, Tìm giá trị nhỏ nhất của biểu thức \(C=\dfrac{1}{\sin^2\alpha}+\dfrac{1}{\sin^2\beta}-2\left(\sin^2\alpha+\sin^2\beta\right)+\dfrac{\sin\alpha}{\tan\alpha}-\dfrac{\tan\alpha+\cos\beta}{\cot\beta}\) .
ii, Tìm điều kiện của \(\Delta OEF\) khi \(2\cos^2\beta-\cot^2\alpha+\dfrac{1}{\sin^2\alpha}=2\).
Cho a, b là 2 số thực dương thỏa mãn a + b ab. Tìm giá trị nhỏ nhất của biểu thức
P
1
a
2
+
2
a
+
1
b
2
+
2
b
+
1
+...
Đọc tiếp
Cho a, b là 2 số thực dương thỏa mãn a + b = ab. Tìm giá trị nhỏ nhất của biểu thức P = 1 a 2 + 2 a + 1 b 2 + 2 b + 1 + a 2 1 + b 2
Áp dụng bất đẳng thức trên ta có ( 1 + a 2 ) ( 1 + b 2 ) ≥ 1 + a b = 1 + a + b (1)
Với mọi x, y > 0, áp dụng bất đẳng thức Côsi cho 2 số dương ta có:
1 x + 1 y ( x + y ) ≥ 2 1 x . 1 y .2 x y = 4 ⇒ 1 x + 1 y ≥ 4 x + y (2)
Áp dụng (1) và (2) ta có:
P ≥ 4 a 2 + 2 a + b 2 + 2 b + 1 + a + b = 4 a 2 + b 2 + 2 a b + 1 + a + b = 4 ( a + b ) 2 + a + b 8 + 7 ( a + b ) 8 + 1
Áp dụng bất đẳng thức Côsi cho 2 số dương ta có:
a + b = a b ≤ ( a + b ) 2 4 ⇒ ( a + b ) 2 ≥ 4 ( a + b ) ⇒ a + b ≥ 4
Áp dụng bất đẳng thức Côsi cho 2 số dương ta có:
4 ( a + b ) 2 + a + b 16 + a + b 16 ≥ 3 4 ( a + b ) 2 . a + b 16 . a + b 16 3 = 3 4 ⇒ P ≥ 3 4 + 7 8 .4 + 1 = 21 4
Dấu bằng xảy ra khi a = b = 2. Vậy giá trị nhỏ nhất của P là 21/4
Đúng 0
Bình luận (0)







