( ab + 13 ) x cd = 2700
( ba + 13 ) x cd = 2160
a - b = 1
chú ý ab và cd là cùng 1 số
Cho hai phép tính sau với a-b=1
(ab+13)*cd=2700
(ba+13)*cd=2160
Hãy tìm ab,cd
Ta có (ab+13)*cd - (ba+13)*cd = 2700-2160 = 540
ab*cd+13*cd - ba*cd - 13*cd = 540
(ab-ba)*cd=540
(10xa+b-10xb-a)*cd=540
9*(a-b)*cd=540
9*1*cd=540 => cd=540:9=60
=> (ab+13)*cd=2700
=> ab+13=2700:60=45 => ab=45-13=32
Trong hai phép tính sau ,với a - b =1
(ab + 13) * cd = 2700
(ba + 13) * cd = 2160
Hãy tìm a, b, c, d ?
Ta có: \(\frac{\overline{ab}+13}{\overline{ba}+13}=\frac{2700}{2160}=\frac{5}{4}\)
<=> 4(ab+13)=5(ba+13)
<=> 4(10a+b+13)=5(10b+a+13)
<=> 40a+4b+4x13=50b+5a+5x13
<=> 35a-46b-13=0 (1)
Mà: a-b=1 => a=b+1. Thay vào (1):
35(b+1)-46b-13=0
<=> 35b+35-46b-13=0 <=> 11b=22 => b=22:11=2
a=b+1=2+1=3
Thay a, b vào trên ta có: (32+13).cd=2700 <=> 45cd=2700 => cd=2700:45=60
=> c=6; d=0
ĐS: a=3; b=2; c=6; d=0
Trong hai phép tính sau ,với a - b = 1
( ab +13) * cd =2700
( ba + 13)*cd =2160
Hãy tìm a,b,c,d?
Trong hai phép tính sau, với a - b = 1 ;
( ab + 13 ) x cd = 2700
( ba +13) x cd
Hãy tìm a, b, c , d
Ta thấy 2700 là có 2 số 0 thì phải nhân cho 100
=> ( ab + 13) = 100 => ab = 87
Vậy ta tìm được a=8 và b=7 thỏa mãn điều kiện a-b =1
=> 100 x cd = 2700 => cd= \(\frac{2700}{100}\)= 27
Vậy ta tìm được c=2 và d=7
Vậy a=8, b=7 ,c =2 và d=7
Còn ( ba + 13) x cd thì a=3, b= 2, c= 7 và d=5
giúp mình với : Tìm a , b , c , d trong phép tính sau : (ab + 13) nhân cd = 2700
tìm ab và cd biết a-b=1 ab x cd=903 ba x cd=516
tìm số ab,cd, biết: ab,cd x 4 = dc, ba
(gợi ý: tìm a trước, rồi tìm d, tìm b dựa vào dấu hiệu chia hết cho 4, và cuối cùng tìm c)
mình nghĩ đề của bạn bị sai ab,cd x 9 mới đúng
Cho từ giác ABCD có \(AB \bot CD;AB = 2;BC = 13;CD = 8;DA = 5\) (H.6.21). Gọi H là giao điểm của AB và CD và đặt x=AH. Hãy thiết lập một phương trình để tính độ dài x, từ đó tính diện tích tứ giác ABCD.
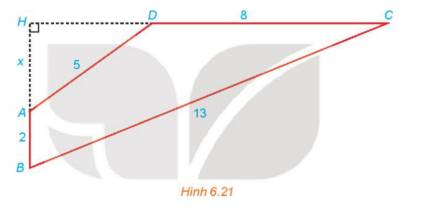
Ta có :AH=x (x>0)
Xét tam giác AHD vuông ở H, ta có:
\(A{D^2} = A{H^2} + H{D^2} \Leftrightarrow H{D^2} = A{D^2} - A{H^2} = 25 - {x^2}\)
\( \Rightarrow HD = \sqrt {25 - {x^2}} \)
Ta có: \(HC = HD + DC = \sqrt {25 - {x^2}} + 8\)
\(HB = AH + AB = x + 2\)
Xét tam giác HBC vuông tại H, ta có:
\(\begin{array}{l}B{C^2} = H{B^2} + H{C^2}\\ \Leftrightarrow {13^2} = {(x + 2)^2} + {\left( {\sqrt {25 - {x^2}} + 8} \right)^2}\\ \Leftrightarrow 169 = {x^2} + 4x + 4 + 25 - {x^2} + 16\sqrt {25 - {x^2}} + 64\\ \Leftrightarrow 16\sqrt {25 - {x^2}} = - 4x + 76\\ \Leftrightarrow 4\sqrt {25 - {x^2}} = - x + 19\end{array}\)
Bình phương hai vế của phương trình trên ta được:
\(\begin{array}{l}16(25 - {x^2}) = {x^2} - 38x + 361\\ \Leftrightarrow 17{x^2} - 38x - 39 = 0\end{array}\)
\( \Leftrightarrow x = 3\) hoặc \(x = \frac{{ - 13}}{{17}}\)
Thay lần lượt các giá trị trên vào phương trình, ta thấy hai giá trị đều thỏa mãn
Do x>0 nên ta chọn x = 3 => AH = 3
\(\begin{array}{l}HD = \sqrt {25 - {3^2}} = 4\\HC = 4 + 8 = 12\\HB = 3 + 2 = 5\end{array}\)
Diện tích tam giác HAD là \({S_1} = \frac{1}{2}.HA.HD = \frac{1}{2}.3.4 = 6\)
Diện tích tam giác HBC là \({S_2} = \frac{1}{2}.HB.HC = \frac{1}{2}.5.12 = 30\)
Vậy diện tích tứ giác ABCD là \(S = {S_2} - {S_1} = 30 - 6 = 24\)
tìm số ab,cd, biết: ab,cd x 4 = dc, ba
(Gợi ý: Tìm a trước, rồi tìm d, tìm b dựa vào dấu hiệu chia hết cho 4, và cuối cùng tìm c)