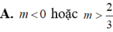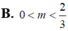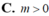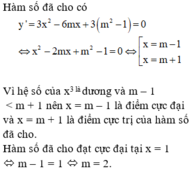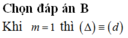Xkm2 + 42dam2 3m2= 7004203m2. Answer :X=

Những câu hỏi liên quan
Tìm tất cả các giá trị thực của m để hàm số
y
x
3
-
3
mx
2
+
3
m
2
-
1
x
-
3
m
2
+
5
đạt cực đại tại x 1. Ta có kết quả: A. m 0 hoặc m 2 B. m 2 C. m 1 D. m 0
Đọc tiếp
Tìm tất cả các giá trị thực của m để hàm số y = x 3 - 3 mx 2 + 3 m 2 - 1 x - 3 m 2 + 5 đạt cực đại tại x = 1. Ta có kết quả:
A. m = 0 hoặc m = 2
B. m = 2
C. m = 1
D. m = 0
25,7 - ( x + 1,05 ) = 38 tìm x
15dam2 3m2 = dam2
2,75 tấn = ... kg
25,7 - (x + 1,05) = 38
(P/S: Bạn xem lại đề bài, lớp 5 chưa học số âm đâu nhé.)
15dam23m2 = 15,03dam2
2,75 tấn = 2750kg
Đúng 1
Bình luận (0)
25,7 - (x + 1,05) = 38
(P/S: Bạn xem lại đề bài, lớp 5 chưa học số âm đâu nhé.)
15dam23m2 = 15,03dam2
2,75 tấn = 2750kg
Đúng 1
Bình luận (0)
Thực hiện phép tính:a)
(
x
+
3
)
3
; b)
x
−
2
5
3
;
c)
3
m...
Đọc tiếp
Thực hiện phép tính:
a) ( x + 3 ) 3 ; b) x − 2 5 3 ;
c) 3 m 2 + n 4 3 ; d) − 2 3 u 3 − 3 2 v 2 3 .
a) x 3 + 9 x 2 + 27x + 27.
b) x 3 − 6 5 x 2 + 12 25 x − 8 125 .
c) 27 m 6 + 27 4 m 4 n + 9 16 m 2 n 2 + n 3 64 .
d) − 8 27 u 9 − 2 u 6 v 2 − 9 2 u 3 v 4 − 27 8 v 6 .
Đúng 0
Bình luận (0)
x2-2(2m+1)x+3m2+6m/x-2=0 có 2 nghiệm x1;x2 thỏa x1+2x2=16
mn giúp với
Cho phương trình 3 x 2 + 2 ( 3 m - 1 ) x + 3 m 2 - m + 1 = 0 . Giải phương trình khi m = -1.
Khi m = -1 phương trình đã cho trở thành 3 x 2 - 8 x + 5 = 0 có hai nghiệm x 1 = 1 , x 2 = 5 / 3
Đúng 0
Bình luận (0)
cho pt x2- 2 ( m+1)x+4m=0 .Tìm m sao cho (x1+m) (x2+m) = 3m2 + 12
Lời giải:
Để pt có 2 nghiệm $x_1,x_2$ thì $\Delta'=(m+1)^2-4m\geq 0$
$\Leftrightarrow (m-1)^2\geq 0$
$\Leftrightarrow m\neq 1$
Khi đó, áp dụng định lý Viet:
$x_1+x_2=2(m+1)$
$x_1x_2=4m$
Khi đó:
$(x_1+m)(x_2+m)=3m^2+12$
$\Leftrightarrow x_1x_2+m(x_1+x_2)+m^2=3m^2+12$
$\Leftrightarrow 4m+2m(m+1)+m^2=3m^2+12$
$\Leftrightarrow 3m^2+6m=3m^2+12$
$\Leftrightarrow 6m=12$
$\Leftrightarrow m=2$ (tm)
Đúng 1
Bình luận (0)
Cho hàm số y=(2m2-4m+7)x+3m2-m-1.Chứng minh hàm số luôn đồng biến R
\(2m^2-4m+7\)
\(=2m^2-4m+2+5\)
\(=2\left(m^2-2m+1\right)+5\)
\(=2\left(m-1\right)^2+5>=5>0\forall m\)
Do đó: Hàm số \(y=\left(2m^2-4m+7\right)x+3m^2-m-1\) luôn đồng biến trên R
Đúng 1
Bình luận (0)
Cho
d
:
x
-
1
2
y
+
2
1
z
-
1
-
1
và
∆
:
x
-
3...
Đọc tiếp
Cho d : x - 1 2 = y + 2 1 = z - 1 - 1 và ∆ : x - 3 m 2 + 1 = y + m 1 = z - 1 . Tìm các giá trị của m để d ∥ ∆ .
![]()
![]()

![]()
Tìm m để
(
C
)
:
2
x
3
-
3
m
2
+
(
m
-
1
)
x
+
1
có 2 điểm cực trị thuộc về 2 phía của đường thẳng y1-x.
Đọc tiếp
Tìm m để ( C ) : 2 x 3 - 3 m 2 + ( m - 1 ) x + 1 có 2 điểm cực trị thuộc về 2 phía của đường thẳng y=1-x.