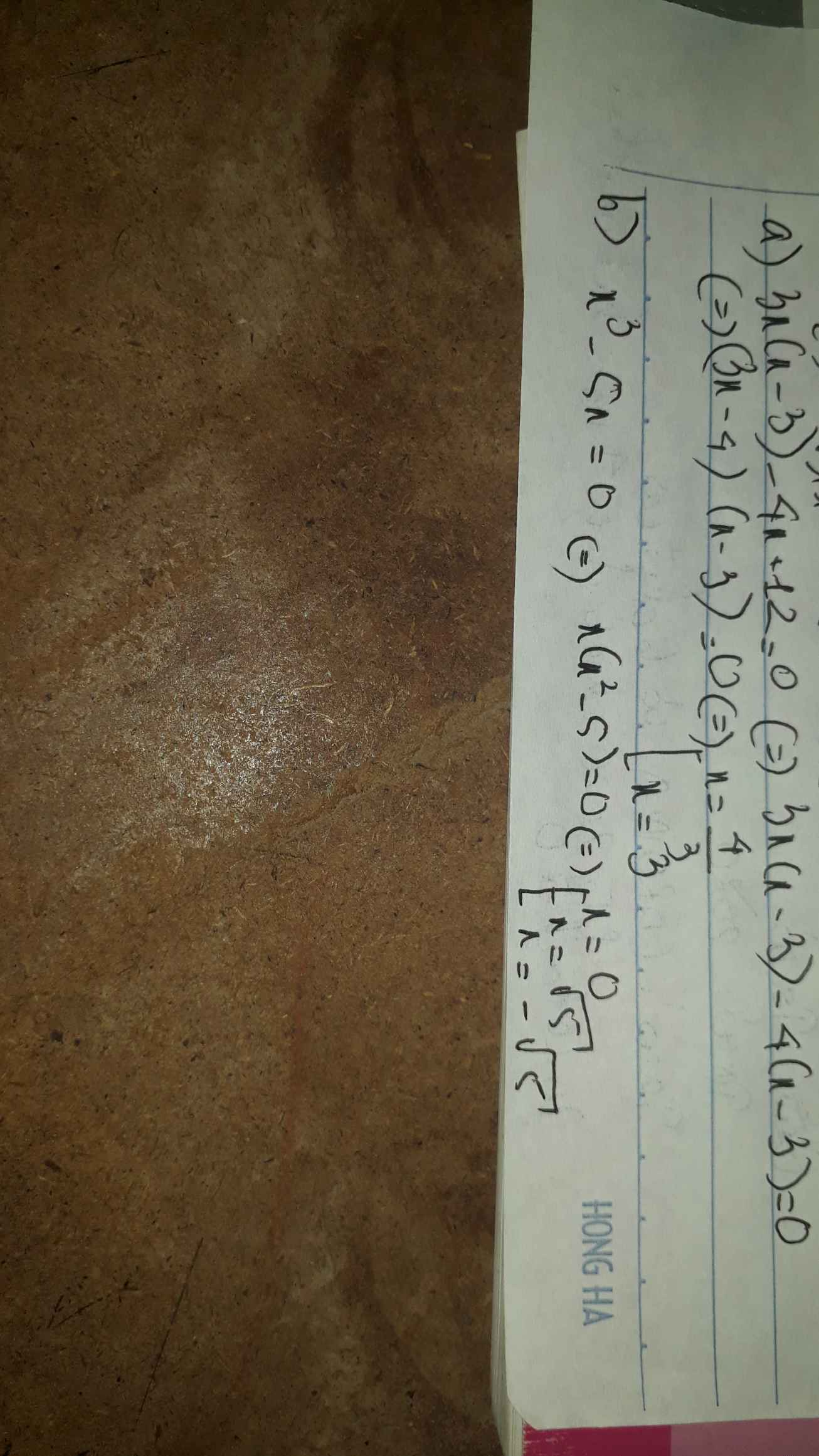0x=4

Những câu hỏi liên quan
3x(x-3)_4x+12=0
x^3-5x=0
(3x-2)^2-(x+2)^2=0
x^2-9-4(x+3)=0
chứng minh rằng với mọi x ϵ R
x^2-8x+17>0
x^2+4x+5>0
x^2-x+1>0
-x^2-4x-5<0
-x^2-3x-4<0
-x^2+10x-27<0
Chứng minh BĐT sau luôn đúng: x > 0
x + \(\dfrac{4}{x}\) \(\ge\) 4
Áp dụng BĐT Cô si ta có: x > 0 => x + \(\dfrac{4}{x}\) \(\ge\) 2 . \(\sqrt{\dfrac{4x}{x}}\)
<=> x + \(\dfrac{4}{x}\) \(\ge\) 4
Đúng 0
Bình luận (0)
Ta có: \(x+\dfrac{4}{x}\ge4\)
\(\Leftrightarrow\dfrac{x^2+4}{x}-\dfrac{4x}{x}\ge0\)
\(\Leftrightarrow x^2-4x+4\ge0\forall x\)
\(\Leftrightarrow\left(x-2\right)^2\ge0\forall x>0\)(luôn đúng)
Đúng 0
Bình luận (0)
`x+4/x>=4`
`<=>x-4+4/x>=0`
`<=>(sqrtx)^2-2.sqrtx. 2/sqrtx+(2/sqrtx)^2>=0(x>0)`
`<=>(sqrtx-2/sqrtx)^2>=0`(luôn đúng)
`=>` đpcm
Dấu "=" `<=>x=2`
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
ai giúp e với
tìm x :
3x ( x + 1 ) - 2x ( x + 2 ) = - 1 - x
4x ( x - 2019 ) - x + 2019 = 0
( x - 4 )^2 - 36 = 0
x^2 + 8x + 16 = 0
x ( x + 6 ) - 7x - 42 = 0
25x^2 - 9 = 0
\(a,PT\Leftrightarrow3x^2+3x-2x^2-4x=-1-x\Leftrightarrow x^2=-1\left(\text{vô nghiệm}\right)\)
Vậy: ...
\(b,PT\Leftrightarrow4x\left(x-2019\right)-\left(x-2019\right)=0\Leftrightarrow\left(x-2019\right)\left(4x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2019\\x=\dfrac{1}{4}\end{matrix}\right.\)
Vậy: ...
\(c,PT\Leftrightarrow\left(x-4-6\right)\left(x-4+6\right)=0\Leftrightarrow\left(x-10\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=10\\x=-2\end{matrix}\right.\)
Vậy: ...
\(d,PT\Leftrightarrow\left(x+4\right)^2=0\Leftrightarrow x=-4\)
Vậy: ...
\(e,PT\Leftrightarrow x\left(x+6\right)-7\left(x+6\right)=0\Leftrightarrow\left(x+6\right)\left(x-7\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-6\\x=7\end{matrix}\right.\)
Vậy: ...
\(f,PT\Leftrightarrow\left(5x-3\right)\left(5x+3\right)=0\Leftrightarrow x=\pm\dfrac{3}{5}\)
Vậy: ...
Đúng 1
Bình luận (1)
Hệ bất phương trình
(
x
+
3
)
(
4
-
x
)
0
x
m...
Đọc tiếp
Hệ bất phương trình ( x + 3 ) ( 4 - x ) > 0 x < m - 1 vô nghiệm khi
A. m ≤ -2
B. m > -2
C. m < 1
D. m > 2
Chọn A
Ta có:
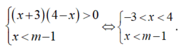
Hệ bất phương trình vô nghiệm khi và chỉ khi m-1≤ -3 hay m≤ - 2.
Đúng 0
Bình luận (0)
Hệ bất phương trình
(
x
+
3
)
(
4
-
x
)
0
x...
Đọc tiếp
Hệ bất phương trình ( x + 3 ) ( 4 - x ) > 0 x < m - 1 vô nghiệm khi
A. m ≤ -2
B. m > -2
C. m < -1
D. m = 0
Chọn A
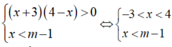
Hệ bất phương trình vô nghiệm khi và chỉ khi m-1≤ -3 hay m≤ -2.
Đúng 0
Bình luận (0)
Hệ bất phương trình
(
x
+
3
)
(
4
-
x
)
0
x
m
-...
Đọc tiếp
Hệ bất phương trình ( x + 3 ) ( 4 - x ) > 0 x < m - 1 vô nghiệm khi
A. m ≤ -2
B. m > -2
C. m < -1
D. m = 0
Chọn A.
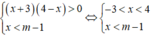
Hệ bất phương trình vô nghiệm m - 1 ≤ -3 ⇔ m ≤ -2
Đúng 0
Bình luận (0)
tìm x
460 + 85 x 4 = ( x + 200) x 4
(x-7)(2x-8)=0
x -280 : 35=5x54
324 + 16x(2x+3)=404
\(460+85\times4=\left(x+200\right)\times4\)
\(\left(x+200\right)\times4=460+340\)
\(\left(x+200\right)\times4=800\)
\(x+200=800:4\)
\(x+200=200\)
\(x=200-200\)
\(x=0\)
~~~
\(\left(x-7\right)\left(2x-8\right)=0\)
\(+, TH1: x - 7 = 0\)
\(x=0+7\)
\(x=7\)
\(+, TH2 : 2x - 8 = 0 \)
\(2x=0+8\)
\(2x=8\)
\(x=8:2\)
\(x=4\)
~~~
\(x-280:35=5\times54\)
\(x-8=270\)
\(x=270+8\)
\(x=278\)
~~~
\(324+16\times\left(2x+3\right)=404\)
\(16\times\left(2x+3\right)=404-324\)
\(16\times\left(2x+3\right)=80\)
\(2x+3=80:16\)
\(2x+3=5\)
\(2x=5-3\)
\(2x=2\)
\(x=2:2\)
\(x=1\)
#\(Toru\)
Đúng 2
Bình luận (0)
`460 + 85 xx 4 = ( x + 200) xx 4`
`460 + 340 = (x+200)xx4`
` 800= (x+200)xx4`
`x+200=800:4`
`x+200=200`
`x=200-200`
`x=0`
__
`(x-7)(2x-8)=0`
`@ TH1`
`x-7=0`
`x=0+7`
`x=7`
`@ TH2`
`2x-8=0`
`2x=0+8`
`2x=8`
`x=8:2`
`x=4`
__
`x -280 : 35=5xx54`
`x -280 : 35=270`
`x-8=270`
`x=270+8`
`x=278`
__
`324 + 16xx(2x+3)=404`
`16xx(2x+3)=404 -324`
`16xx(2x+3)=80`
`2x+3=80:16`
`2x+3=5`
`2x=5-3`
`2x=2`
`x=2:2`
`x=1`
Đúng 2
Bình luận (0)
với mỗi điểm khác điểm ở trên tia 0x với 100 điểm khác điểm 0 trên tia 0x thì tạo thành bao tia 0x
Xem thêm câu trả lời