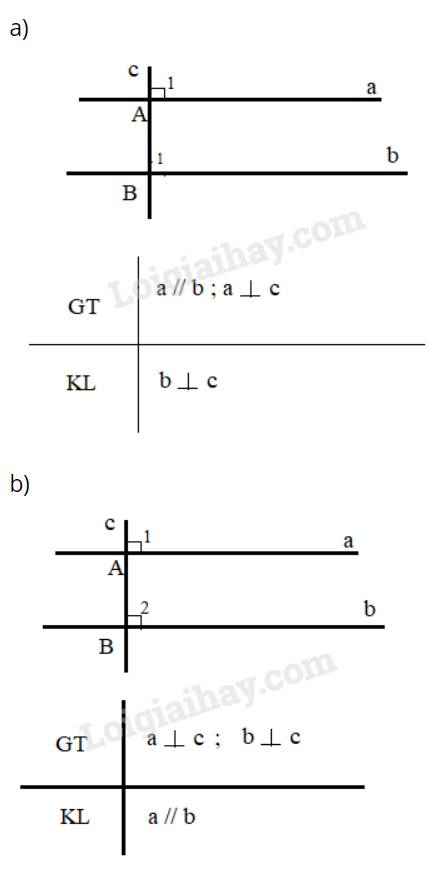
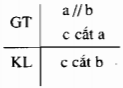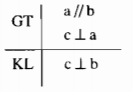chứng minh định lí sau :nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại

Những câu hỏi liên quan
Vẽ hình, viết giả thiết, kết luận bằng kí hiệu và chứng minh định lí: " Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng sẽ vuông góc với đường thẳng còn lại."
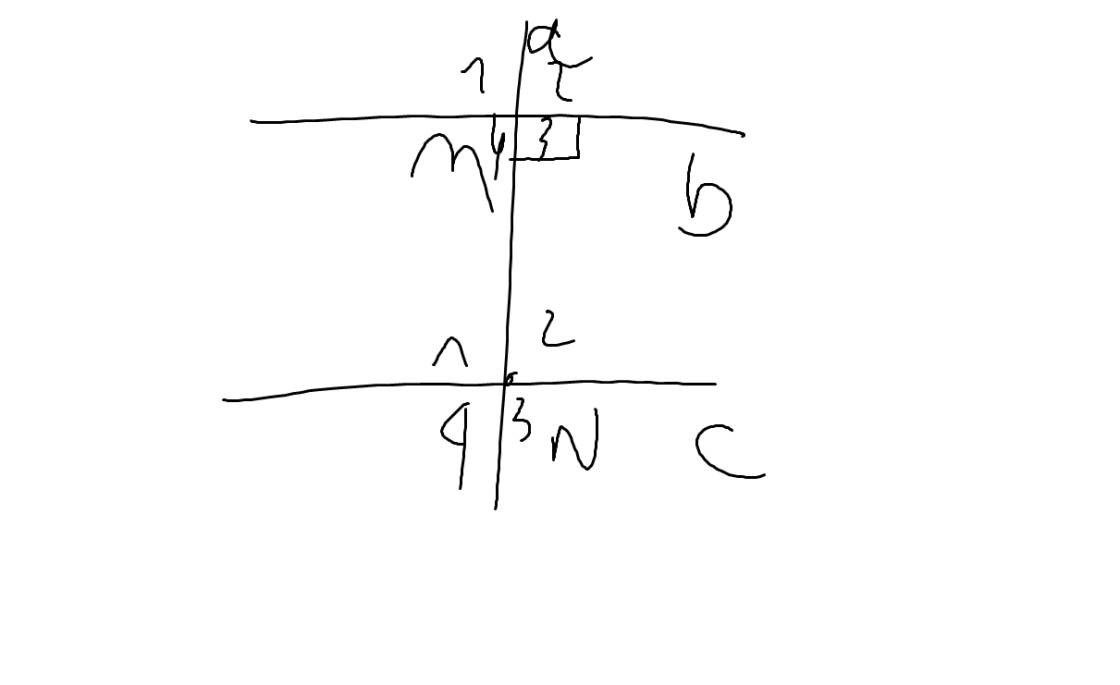
| GT | a\(\perp\)b tại M a cắt c tại N b//c |
| KL | a\(\perp\)c tại N |
Chứng minh định lí:
Ta có: b//c
=>\(\widehat{M_3}=\widehat{N_1}\)(hai góc so le trong)
mà \(\widehat{M_3}=90^0\)
nên \(\widehat{N_1}=90^0\)
=>a\(\perp\)c tại N
Đúng 0
Bình luận (0)
Chứng minh định lý:
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại.
Từ t/c :
Nếu đường thẳng a và đường thẳng b cùng vuông góc với 1 đường thẳng thì hai đường thẳng a và đường thẳng b song song với nhau.
=> đpcm.
Đúng 1
Bình luận (0)
Ta có : \(x||y\left(gt\right)\)
\(\Rightarrow\widehat{A_1}=\widehat{B_1}\)( hai góc so le trong )
Mà \(\widehat{A_1}=90^o\)
\(\Rightarrow\widehat{B_1}=90^o\)
Hay \(AB\perp y\)
Đúng 1
Bình luận (0)
Hãy chứng minh định lí nói ở Ví dụ trang 56: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”. Trong chứng minh đó, ta đã sử dụng những điều đúng đã biết nào?
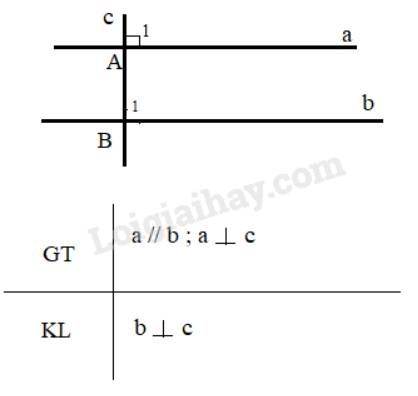
Giả sử cho 2 đường thẳng song song a và b, đường thẳng c vuông góc với a. Ta phải chứng minh c cũng vuông góc với b. Thật vậy:
Vì a//b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) ( 2 góc đồng vị), mà \(\widehat {{A_1}} = 90^\circ \) nên \(\widehat {{B_1}} = 90^\circ \) hay \(b \bot c\)
Vậy một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại.
Trong chứng minh trên, ta đã sử dụng tính chất của hai đường thẳng song song.
Đúng 0
Bình luận (0)
Vẽ hình, viết giả thiết, kết luận của định lí: “ Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”.

Giả sử cho 2 đường thẳng song song a và b, đường thẳng c vuông góc với a. Ta phải chứng minh c cũng vuông góc với b.
Thật vậy,
Vì a//b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) ( 2 góc đồng vị), mà \(\widehat {{A_1}} = 90^\circ \)nên \(\widehat {{B_1}} = 90^\circ \) hay \(b \bot c\)(đpcm)
Đúng 1
Bình luận (0)
Vẽ hình và viết giả thiết, kết luận của các định lí sau :
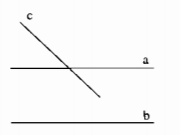
a) Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cắt đường thẳng kia
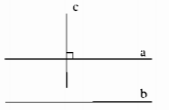
b) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia
Bài 18: Vẽ hình minh họa và viết GT, KL cho các định lí sau:a) Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.b) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thăng kia.c) Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.d) Hai góc đối đỉnh thì bằng nhau
Đọc tiếp
Bài 18: Vẽ hình minh họa và viết GT, KL cho các định lí sau:
a) Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
b) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thăng kia.
c) Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
d) Hai góc đối đỉnh thì bằng nhau
d:
Giả thiết: \(\widehat{xAy}\) và \(\widehat{x'Ay'}\) là hai góc đối đỉnh
Kết luận: \(\widehat{xAy}=\widehat{x'Ay'}\)
Đúng 1
Bình luận (0)
Vẽ hình minh họa và viết giả thiết, kết luận bằng kí hiệu cho mỗi định lí sau:a) Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lạib) Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.c) Qua một điểm cho trước có duy nhất một đường thẳng vuông góc với đường thẳng cho trước.
Đọc tiếp
Vẽ hình minh họa và viết giả thiết, kết luận bằng kí hiệu cho mỗi định lí sau:
a) Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại
b) Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.
c) Qua một điểm cho trước có duy nhất một đường thẳng vuông góc với đường thẳng cho trước.
bài 1: vẽ hình và viết GT,KL các định lí sau bằng kí hiệu.a) Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cùng vuông góc với đường thẳng kiab) Nếu 1 đường thẳng cắt hai đường thẳng song song thì 2 góc đồng vị bằng nhaumong các bạn giúp đỡ
Đọc tiếp
bài 1: vẽ hình và viết GT,KL các định lí sau bằng kí hiệu.
a) Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cùng vuông góc với đường thẳng kia
b) Nếu 1 đường thẳng cắt hai đường thẳng song song thì 2 góc đồng vị bằng nhau
mong các bạn giúp đỡ
Bài 1. Cho định lí:” Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia”.
Hãy vẽ hình minh họa định lí đó và viết giả thiết, kết luận bằng kí hiệu.
Các bạn giúp mik bài này với:
Vẽ hình và ghi GT-KL và chứng minh định lý sau:
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại
mik mới lập nick nên mn nhớ kb mik nha
giả thiết: 1 đường thẳng vuông góc với một trong 2 đường thẳng
kết luận: nó vuông góc với đường thẳng còn lại.
BẬT MÍ CHO BẠN NÈ: GIẢ THIẾT LÀ NHỮNG CHỮ Ở SAU TỪ ''NẾU''
KẾT LUẬN LÀ NHỮNG CHỮ SAU TỪ THÌ
Đúng 0
Bình luận (0)