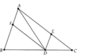
5. cho ABC và phân giác AD. Qua D kẻ đường thẳng song song với AC cắt AB tại E và qua D kẻ đường thẳng song song với AB cắt AC tại F. Chứng minh È là phân giác AED
6. cho ABC cân tại A và trung tuyến AM. qua M kẻ đương thẳng song song với AB cắt AC tại Q
a, tứ giác APMQ là hình gì? Vì sao ?
b, chứng minh PQ//BC