cho tam giác cân tại A E,F,D là TĐ AB,BC,AC CM ADEF LÀ HÌNH THOI

Những câu hỏi liên quan
Cho tam giác ABC cân tại A. Gọi D, E, F theo thứ tự là trung điểm của AB, BC, AC. Chứng minh rằng ADEF là hình thoi
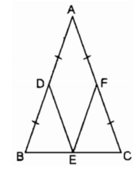
Ta có: E là trung điểm của BC (gt)
D là trung điểm của AB (gt) nên ED là đường trung bình của ∆ ABC
DE = AF = 1/2 AC (1)
F là trung điểm của AC (gt) nên EF là đường trung bình ∆ ABC ⇒ EF = AD = 1/2 AB (2)
AB = AC (gt)
Từ (1), (2) và (gt) suy ra: AD = DE = EF = AF
Vậy tứ giác ADEF là hình thoi.
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A. Gọi D;E;F theo thứ tự là trung điểm các cạnh AB,BC,CA.Chứng minh rằng tứ giác ADEF là hình thoi.
Cho tam giác ABC cân tại A. Gọi D, E, F theo thứ tự là trung điểm của AB, BC, AC
a) Chứng minh rằng ADEFF là hình thoi
b) Tam giác ABC có thêm điều kiện gì thì ADEF là hình vuông
a) Tứ giác ADEF có bốn cạnh bằng nhau nên là hình thoi.
b) Hình thoi ADEF là hình vuông \(\Leftrightarrow\widehat{A}=90^o\Leftrightarrow\Delta ABC\) vuông cân tại A.
Đúng 0
Bình luận (0)
Bài 3. Cho tam giác ABC cân tại A. Gọi D, E, F theo thứ tự là trung điểm của AB, BC, AC. Gọi M là điểm đối xứng với E qua F
a) ADEF là hình thoi
b) AECM là hình chữ nhật
c) AE, DF, BM đồng qui
d) Tam giác ABC có thêm điều kiện gì để ADEF là hình vuông
Cho tam giác ABC vuông tại A (AB<AC ) . E là trung điểm của BC . Kẽ EF vuông góc với AB tại F , ED vuông góc với AC tại D
a) chứng minh tứ giác ADEF là hình chữ nhật
b) Gọi K là điểm đối xứng của E qua D . Chứng minh tứ guacs AECK là hình thoi
a) Xét tứ giác ADEF có : góc A = 90 độ ( tam giác ABC vuông tại A)
góc EFA = 90 độ ( EF vuông góc với AB tại F)
góc EDA = 90 ( ED vuông góc với AC tại D)
suy ra : ADEF là hcn
b) Xét tam giác ABC có : BE = EC ( E là trung điểm của BC )
ED song song với AB ( EFAD là hcn )
suy ra : AD = DC
Xét tứ giác AECK có : ED = DK ( E đối xứng với K qua D )
AD = DC (cmt)
suy ra : tứ giác AECK là hình bình hành
mà ED vuông góc với AC
suy ra : hbh AECK là hình thoi
Đúng 1
Bình luận (0)
a) Xét tứ giác ADEF có : góc A = 90 độ ( tam giác ABC vuông tại A)
góc EFA = 90 độ ( EF vuông góc với AB tại F)
góc EDA = 90 ( ED vuông góc với AC tại D)
=> ADEF là hcn
b) Xét tam giác ABC có : BE = EC ( E là trung điểm của BC )
ED song song với AB ( EFAD là hcn )
=> AD = DC
Xét tứ giác AECK có : ED = DK ( E đối xứng với K qua D )
AD = DC (cmt)
=> tứ giác AECK là hình bình hành
Mà ED vuông góc với AC
=> hbh AECK là hình thoi
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Gọi D, E, F theo thứ tự là trung điểm của AB, BC, AC. Tam giác ABC có thêm điều kiện gì thì ADEF là hình vuông ?
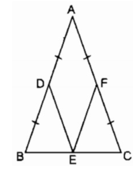
Hình thoi ADEF là hình vuông ⇒ ∠ A = 90 0
⇒ ∆ ABC vuông cân tại A
Ngược lại nếu ∆ ABC vuông cân tại A
⇒ Tứ giác ADEF là hình thoi có ∠ A = 90 0
⇒ Hình thoi ADEF là hình vuông
Vậy hình thoi ADEF là hình vuông thì ∆ ABC vuông cân tại A.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A . Gọi D , E , F theo thứ tự là trung điểm các cạnh AB , BC , CA . Chứng minh rằng :
a/ BDFC là hình thang cân
b/ ADEF là hình thoi
tam giác ABC cân (AB=AC) gọi D,E,F là trung điểm của AB,BC,CA . trên tia EF lấy M sao cho F là trung điểm EM
a, BDFC là hình gì?
b, ADEF là hình thoi
c, AECM là hcn
Cho tam giác ABC gọi D,E,F lần lượt là trung điểm của AB,BC,AC.
a) Chứng minh tứ giác ADEF là hình bình hành.
b) Tìm điều kiện của tam giác ABC để tứ giác ADEF là hình thoi.
a,Ta có: FA=FC=AC:2(gt)
EC=EB=BC:2(gt)
=>FE là đường TB của tam giác ABC => EF//AD
CMTT: DE//FA
=> ADEF là hình bình hành
b,ADEF LÀ HÌNH thoi => AF = AD
=> AC=AB =>ABC là tam giác cân
Vậy đấy dễ mà tick cko mk nha!!!
Đúng 0
Bình luận (0)
a.
Xét tam giác ABC có
AF = FC
BE = EC
=>FE là đường trung bình của tam giác ABC ( tính chất )
=> FE // AB mà D thuộc AB nên FE // AD (1)
Xét tiếp tam giác ABC có
DB = AD
BE = EC
=> DE là đường trung bình của tam giác ABC ( tính chất )
=> DE // AC mà F thuộc AC nên DE // AF (2)
Từ (1) và (2) => Tứ Giác ADEF là hình bình hành ( dấu hiệu ) ( đpcm)
b.
Để Tứ Giác ADEF là hình chữ nhật thì góc DAE = 90 độ ( hay góc BAC = 90 độ ) DE và EF phải lần lượt là trung trực của AB và AC, DE và EF phải giao nhau tại trung điểm của BC ( là điểm E )
1 . Cho tam giác giác ABC cân tại A , trung tuyến AM . Gọi D là điểm đối xứng với A qua M và K là trung điểm của MC , E là điểm đối xứng của D qua K .a . Chứng minh tứ giác ABCD là hình thoi b . Tứ giác AMCE là hình gì ?c . AM cắt BE { I } . Chứng minh I là trung điểm của BEd . CMR : AK , CI , EM đồng qui2 . Cho tam giác ABC cân tại A ( AB AC ) . Gọi D , E , F theo thứ tự là trung điểm của các cạnh AB , BC , CA . CMR :a . Tứ giác BDFC là hình thang cân b . Tứ giác ADEF là hình thoi c . Tìm đi...
Đọc tiếp
1 . Cho tam giác giác ABC cân tại A , trung tuyến AM . Gọi D là điểm đối xứng với A qua M và K là trung điểm của MC , E là điểm đối xứng của D qua K .
a . Chứng minh tứ giác ABCD là hình thoi
b . Tứ giác AMCE là hình gì ?
c . AM cắt BE = { I } . Chứng minh I là trung điểm của BE
d . CMR : AK , CI , EM đồng qui
2 . Cho tam giác ABC cân tại A ( AB = AC ) . Gọi D , E , F theo thứ tự là trung điểm của các cạnh AB , BC , CA . CMR :
a . Tứ giác BDFC là hình thang cân
b . Tứ giác ADEF là hình thoi
c . Tìm điều kiện của tam giác ABC để tứ giác ADEF là hình vuông .
Bài 2:
a: Xet ΔABC có AD/AB=AF/AC
nen DF//BC và DF=1/2BC
=>BDFC là hình thang
mà góc B=góc C
nên BDFC là hình thang cân
b Xet ΔABC có
CE/CB=CF/CA
nên EF//AB và EF=AB/2
=>EF//AD và EF=AD
=>ADEF là hình bình hành
mà AD=AF
nen ADEF là hình thoi
c: Để ADEF là hình vuông thì góc BAC=90 độ
Đúng 0
Bình luận (0)





















