Tọa độ giao điểm của (d1) và (d2) là:

\(\left\{{}\begin{matrix}2x+3=x-4\\y=x-4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x-x=-4-3=-7\\y=x-4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=-7\\y=-7-4=-11\end{matrix}\right.\)

Thay x=-7 và y=-11 vào (d3), ta được:

-7m+m+1=-11

=>-6m=-11-1=-12

=>m=12/6=2

Xét pthđ giao điểm của d1 và d2
x-4=2x+3
<=> x= -7
Thay x=-7 vào d1 
y=-7-4=-11 => A(-7:-11) là giao điểm d1 và d2
Thay x=-7 vào d3 -> y=m(-7)+m+1=-6m+1=-11
- Để d1 d2 d3 đq -> A \(\in\)d3
-> -6m+1=-11
-6m=-12
m=2 
Vậy m=2 thì 3 đường thẳng d1 , d2 , d3 đq 
chúa bạn học tốt

tks Anhh

No prbls :)

b) d 1  cắt trục hoành tại điểm có hoành độ bằng – 3 khi:

0 = -3m + 2m - 1 ⇔ -m - 1 = 0 ⇔ m = -1

Vậy với m = -1 thì  d 1  cắt trục hoành tại điểm có hoành độ bằng – 3

Tọa độ giao điểm của (d1) và (d2) là:

\(\left\{{}\begin{matrix}x-1=-x+3\\y=x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

Thay x=2 và y=1 vào (d3),ta được

2m-2-m=1

=>m-2=1

hay m=3

Lời giải:

Giao điểm của 2 đường thẳng thuộc trục hoành nên có dạng $(a,0)$. Vì điểm này thuộc $(d_1):x+y=-1$ nên $a+0=-1\Rightarrow a=-1$

Vậy giao điểm của 2 ĐT trên là $(-1,0)$

Giao điểm này $\in (d_2)$ khi mà $m.(-1)+0=1$

$\Leftrightarrow m=-1$

1: d1: y=mx-m+1

=m(x-1)+1

Điểm mà (d1) luôn đi qua có tọa độ là:

x-1=0 và y=1

=>x=1 và y=1

2: Tọa độ giao điểm của (d2) và (d3) là:

2x+3=x+1 và y=x+1

=>x=-2 và y=-1

Thay x=-2 và y=-1 vào (d1), ta được:

-2m-m+1=-1

=>-3m=-2

=>m=2/3

Để hai đường thẳng vuông góc thì m(2m-3)=-1

\(\Leftrightarrow\left(m-1\right)\left(2m-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}m=1\\m=\dfrac{1}{2}\end{matrix}\right.\)

Đáp án B

+Giao điểm của d₁ và d₂ là nghiệm của hệ:

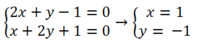
Vậy 2 đường thẳng d₁ và d₂ tại A( 1 ; -1) .

+Để 3 đường thẳng đã cho  đồng quy thì d₃ phải đi qua điểm A nên tọa độ A  thỏa phương trình d₃

Suy ra : m+ 1-7= 0 hay m= 6.

Chọn B.

Gọi M(xM; yM) là giao điểm của d1 và d2. Khi đó, tọa độ giao điểm M của d1 và d2 là nghiệm của hệ phương trình:

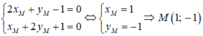
Để 3 đường thẳng d1, d2, d3 đồng quy thì M(1;-1) ∈ (d3): mx - y - 7 = 0, nên ta có:

m.1 - (-1) - 7 = 0 ⇔ m + 1 - 7 = 0 ⇔ m - 6 = 0 ⇔ m = 6

Vậy 3 đường thẳng d1, d2, d3 đồng quy.