y x 10 = 100 x 2

Những câu hỏi liên quan
Tìm x và y biết :
1) x/3 = y/4 và x^2 + y^2 = 100
2) x/4 = y/3 và x.y = 10
3) x/5 = y/3 và x^2 -y^3 =1 6
4) x/2 = y/5 và x.y = 10
5) x/5 = y/4 và x^2 . y =100
6) 4x = 3y và x^2 + y^2 =100
7) x/3 = y/7 và x^2 + y^2 = 58
8) x/3 = y/4 và 2x^2 -3y^2 = -120
9) x/3 = y/2 và 3x^2 - 5y^2 = -20
( 2 x - 3 ) ^ 10 + ( x + 2 y ) 100 ^ 100 _< 0
Tìm x và y.
Ta có \(\hept{\begin{cases}\left(2x-3\right)^{10}\ge0\forall x\\\left[100\left(x+2y\right)\right]^{100}\ge0\forall x;y\end{cases}}\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}2x-3=0\\x+2y=0\end{cases}}\Rightarrow\hept{\begin{cases}x=1,5\\y=-0,75\end{cases}}\)
Vậy x = 1,5 ; y = -0,75
\(\left(2x-3\right)^{10}+\left(x+2y\right)^{100}\le0\)
Ta có: \(\left(2x-3\right)^{10}\)và \(\left(x+2y\right)^{100}\) là số chính phương. => \(\left(2x-3\right)^{10}\ge0;\left(x+2y\right)^{100}\ge0\)
Mà \(\left(2x-3\right)^{10}+\left(x+2y\right)^{100}\le0\)
=> \(\left(2x-3\right)^{10}=0;\left(x+2y\right)^{100}=0\)
=> 2x - 3 = 0; x + 2y = 0. => x = 3/2; y = -3/4.
B1: Tìm x, y biết:
(x-1/2+y)^2 + (x+1/3-y)^2 = 0
B2: So sánh
a)2^91 và 5^35
b)54^4 và 21^12
c)2^100 và 10^30
D)2^100 và 10^31
Tìm x,y thuộc Z biết :
(x+y-10)2 + (y+z-20) + (x+z+100)
1.Tìm P
P;P+10;P+14 đều là số nguyên tố.
2.Tìm x,y
(2.x+1).(y-3)=10
3.Tìm x
(x+1)+(x+2)+(x+3)+...+(x+100)=5057
1.Thử với p=2 ko được.
Thử với p=3 được.
Thử với >3 là 3k+1 và 3k+2.
=>p=3.
2.Phân tích 10 ra thừa số nguyên tố rồi kẻ bảng.
3.Tách riêng x và số ra.
Đúng 0
Bình luận (0)
Tìm M biết: 65*X+10=100*4, Y+13=X*7, Z=T+X=80:2, X*Y-T+Z=M
Tìm x,y thuộc Z biết :
(x+y-10)2 + (y+z-20) + (x+z+100)=0
Vẽ các elip sau
a) \(\frac{{{x^2}}}{{10}} + \frac{{{y^2}}}{4} = 1\)
b) \(\frac{{{x^2}}}{{12}} + \frac{{{y^2}}}{3} = 1\)
c) \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\)
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình elip theo cú pháp x^2/10 + y^2/4 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
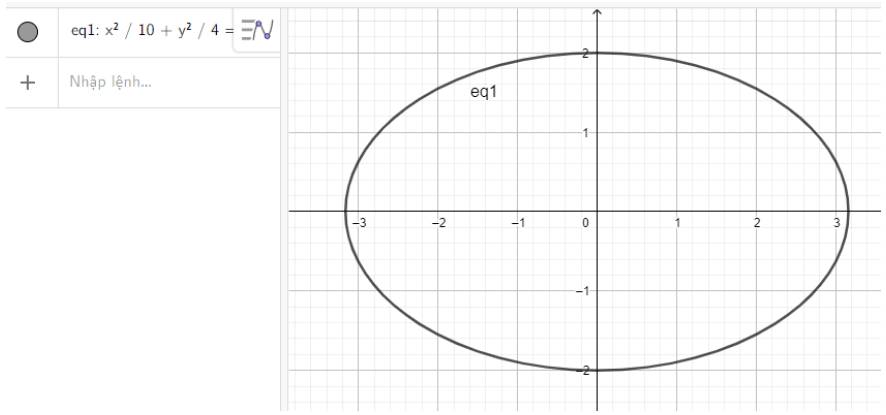
b) Nhập phương trình elip theo cú pháp x^2/12 + y^2/3 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
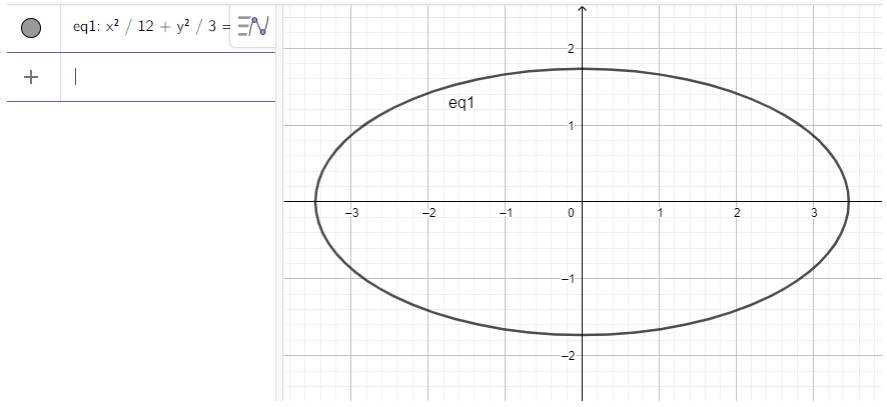
c) Nhập phương trình elip theo cú pháp x^2/100 + y^2/36 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
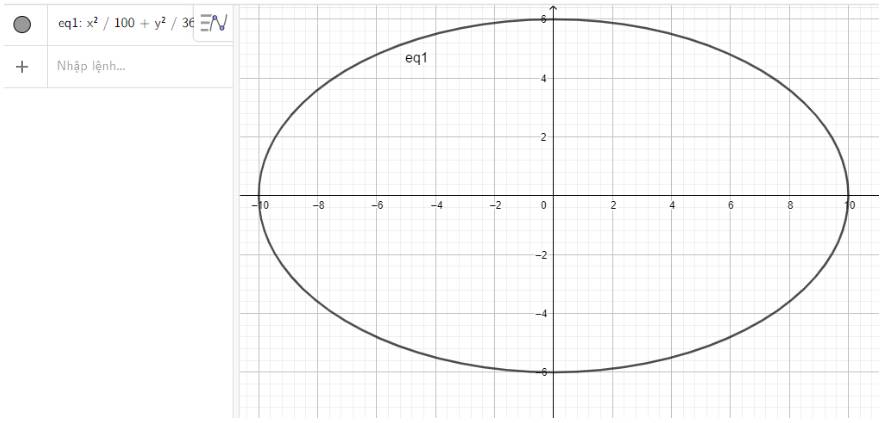
Đúng 0
Bình luận (0)
Bài 3: Tính giá trị biểu của biểu thức:
A= (1^2 + 2^2 + 3^2 + ... + 100^2) (2x - y^3) phần x^10 + y^10
tại x = 13,5 ; y = 3
tại x = 13,5 ; y = 3 ta có:
2x - y^3 = 2.13,5 - 3^3 = 0
A = 0















