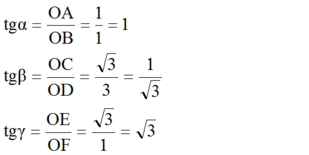Gọi β là góc tạo bởi đường thẳng (d): y = -2016(x - 20152013) + 20142013 và trục Ox.
Khi đó tan(180o - β) = .............

Những câu hỏi liên quan
Gọi α,β lần lượt là hai góc tạo bởi hai đường thẳng y=-2018x+9 và y=-2019x+10 với trục Ox.Khi đó
A.α<β<900 B.β<α<900 C.900<α<β D.900<β<α
12. Gọi α, β lần lượt là góc tạo bởi hai đường thẳng (d): y √3x − 1 và đường thẳng(d′): y −2x − 1 với chiều dương của trục Ox. Khẳng định nào sau đây đúng?Gọi α, β lần lượt là góc tạo bởi hai đường thẳng (d): y √3x − 1 và đường thẳng(d′): y −2x − 1 với chiều dương của trục Ox. Khẳng định nào sau đây đúng?A. α β 900 B. β α 900C. α 900 βD. β 900 α
Đọc tiếp
12. Gọi α, β lần lượt là góc tạo bởi hai đường thẳng (d): y = √3x − 1 và đường thẳng
(d′): y = −2x − 1 với chiều dương của trục Ox. Khẳng định nào sau đây đúng?
Gọi α, β lần lượt là góc tạo bởi hai đường thẳng (d): y = √3x − 1 và đường thẳng
(d′): y = −2x − 1 với chiều dương của trục Ox. Khẳng định nào sau đây đúng?
A. α < β < 900 B.
β < α < 900
C. α < 900 < β
D. β < 900 < α
Gọi
α
và
β
lần lượt là góc tạo bởi đường thẳng y - 2x + 1 và y - 5x + 2 với trục Ox. Khẳng định nào sau đây là đúng : A.
90
°
β
α
B.
90
°
α
β
C.
α
β
90
°
D.
β
α
90
°
Đọc tiếp
Gọi α và β lần lượt là góc tạo bởi đường thẳng y = - 2x + 1 và y = - 5x + 2 với trục Ox. Khẳng định nào sau đây là đúng :
A. 90 ° < β < α
B. 90 ° < α < β
C. α < β < 90 °
D. β < α < 90 °
Đáp án A
Hai đường thẳng đã cho có hệ số góc lần lượt là – 2 < 0 và -5 < 0
Góc tạo bởi hai đường thẳng đã cho với trục Ox là góc tù.
Lai có: -5 < -2 nên β < α
Vậy 90 ° < β < α
Đúng 0
Bình luận (0)
Cho đồ thị hai hàm số y x +100 và y 3x + 1. Gọi
α
;
β
lần lượt là góc tạo bởi hai đường thẳng đã cho với trục Ox. Tìm khẳng định đúng. A.
90
°
β
α
B.
90
°
α
β
C.
α
β
90
°
D.
α
90
°
β
Đọc tiếp
Cho đồ thị hai hàm số y = x +100 và y = 3x + 1. Gọi α ; β lần lượt là góc tạo bởi hai đường thẳng đã cho với trục Ox. Tìm khẳng định đúng.
A. 90 ° < β < α
B. 90 ° < α < β
C. α < β < 90 °
D. α < 90 ° < β
Đáp án C
Hai đường thẳng y = x + 100 và y = 3x + 1 có hệ số góc lần lượt là a = 1 > 0 và a’ = 3 > 0
Suy ra: góc tạo bởi mỗi đường thẳng và trục Ox là góc nhọn.
Lại có: 1 < 3 nên α < β
Vậy α < β < 90 °
Đúng 0
Bình luận (0)
a) Vẽ đồ thị của các hàm số
y
x
+
1
;
y
1
3
x
+
3
;
y
3
x
−
3
b) Gọi α, β, γ lần lượt là các góc tạo bởi các đường thẳng trên trục Ox.Chứng minh rằng
tg
α
1
,
tg
β
1
3
,
tg
γ
3
Tính...
Đọc tiếp
a) Vẽ đồ thị của các hàm số
y = x + 1 ; y = 1 3 x + 3 ; y = 3 x − 3
b) Gọi α, β, γ lần lượt là các góc tạo bởi các đường thẳng trên trục Ox.
Chứng minh rằng
tg α = 1 , tg β = 1 3 , tg γ = 3
Tính số đo các góc α, β, γ.
a) - Với hàm số y = x + 1
Cho x = 0 y = 1 được A(0; 1)
Cho y = 0 x = -1 được B(-1; 0)
Nối A, B được đường thẳng y = x + 1
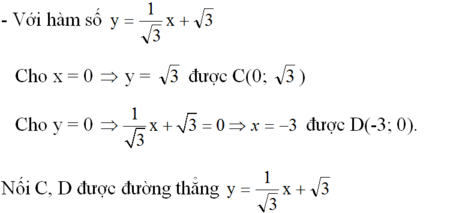
- Với hàm số y = √3 x - √3
Cho x = 0 => y = -√3 được E(0; -√3)
Cho y = 0 => x = 1 được F(1; 0).
Nối E, F được đường thẳng y = √3 x - √3
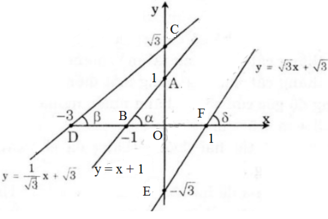
b) Ta có:
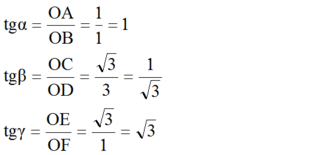
Suy ra α = 45o, β = 30o, γ = 60o
Đúng 0
Bình luận (0)
Gọi α, β, γ lần lượt là các góc tạo bởi các đường thẳng trên trục Ox.
Chứng minh rằng t g α = 1 , t g β = 1 3 , t g γ = 3
Tính số đo các góc α, β, γ.
Trong không gian với hệ trục tọa độ Oxyz, gọi (α) là mặt phẳng chứa đường thẳng
∆
:
x
-
2
1
y
-
1
1
z
-
2
và vuông góc với mặt phẳng (β):x+y+2z+10. Khi đó giao tuyến của hai mặt phẳng (α), (β) có phương trình A. ...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, gọi (α) là mặt phẳng chứa đường thẳng ∆ : x - 2 1 = y - 1 1 = z - 2 và vuông góc với mặt phẳng (β):x+y+2z+1=0. Khi đó giao tuyến của hai mặt phẳng (α), (β) có phương trình
A. x - 1 = y + 1 1 = z - 1
B. x 1 = y + 1 1 = z - 1 1
C. x - 2 1 = y + 1 - 5 = z 2
D. x + 2 1 = y - 1 - 5 = z 2
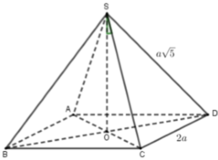
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a và cạnh bên bằng
a
5
. Gọi (P) là mặt phẳng đi qua A và vuông góc với SC. Gọi
β
là góc tạo bởi mp (P) và (ABCD). Tính tan
β
A.
tan
β
6
3
B.
tan
β
6
2...
Đọc tiếp
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a và cạnh bên bằng a 5 . Gọi (P) là mặt phẳng đi qua A và vuông góc với SC. Gọi β là góc tạo bởi mp (P) và (ABCD). Tính tan β
A. tan β = 6 3
B. tan β = 6 2
C. tan β = 2 3
D. tan β = 3 2
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a và cạnh bên bằng
a
5
. Gọi (P) là mặt phẳng đi qua A và vuông góc với SC. Gọi
β
là góc tạo bởi mp (P) và (ABCD). Tính tan
β
A. tan
β
6
3
B. tan
β
6
2
C. tan
β
...
Đọc tiếp
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a và cạnh bên bằng a 5 . Gọi (P) là mặt phẳng đi qua A và vuông góc với SC. Gọi β là góc tạo bởi mp (P) và (ABCD). Tính tan β
A. tan β = 6 3
B. tan β = 6 2
C. tan β = 2 3
D. tan β = 3 2
Phương pháp:
Sử dụng lý thuyết: Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng ấy.
Cách giải:

Gọi O là tâm hình vuông ABCD.
Ta có: 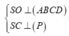
=> góc giữa (ABCD) và (P) là góc giữa SC và SO hay SCO.
Hình vuông ABCD cạnh 2a nên ![]()
Tam giác SOC vuông tại O nên
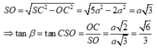
Chọn: A
Đúng 0
Bình luận (0)