gup mk vs
1/x=3/2 . 1/y
1/x + 1/y =1/24
giải hệ phương trình bằng cách đặt ẩn dụ
Những câu hỏi liên quan
\(\hept{\begin{cases}\frac{1}{x}=\frac{3}{2}\cdot\frac{1}{y}\\\frac{1}{x}+\frac{1}{y}=\frac{1}{24}\end{cases}}\)
giaỉ hệ phương trình bằng cách đặt ẩn dụ
Đặt: \(\hept{\begin{cases}\frac{1}{x}=a\\\frac{1}{y}=b\end{cases}}\)thì hệ thành
\(\hept{\begin{cases}a=\frac{3b}{2}\\a+b=\frac{1}{24}\end{cases}}\)
Rồi giải tiếp đi b
Đúng 0
Bình luận (0)
nhung mk vẫn chưa hiểu lắm bạn giải tiếp cho mk dc ko
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải hệ phương trình (II) bằng cách đặt ẩn phụ ( u 1/x; v 1/y) rồi trả lời bài toán đã cho.
I
I
1
x
3
2
.
1
y
1...
Đọc tiếp
Giải hệ phương trình (II) bằng cách đặt ẩn phụ ( u = 1/x; v = 1/y) rồi trả lời bài toán đã cho. I I 1 x = 3 2 . 1 y 1 x + 1 y = 1 24
Đặt 1/x = u; 1/y = v,hệ (II)trở thành:
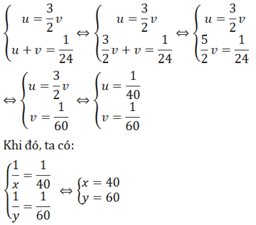
Vậy số ngày để đội A làm 1 mình xong đoạn đường đó là 40 ngày
Số ngày để đội B làm 1 mình xong đoạn đường đó là 60 ngày
Đúng 0
Bình luận (0)
\(\sqrt[4]{x}=\dfrac{1}{\sqrt[4]{2}}-\sqrt{\dfrac{1}{1+\sqrt{2}}-x}\)
Giải phương trình bằng cách đặt ẩn phụ đưa về hệ phương trình
Giải hệ phương trình (II) bằng cách đặt ẩn phụ ( u 1/x; v 1/y) rồi trả lời bài toán đã cho.
(
I
I
)
1
x
3
2
⋅
1
y
1
x
+...
Đọc tiếp
Giải hệ phương trình (II) bằng cách đặt ẩn phụ ( u = 1/x; v = 1/y) rồi trả lời bài toán đã cho.
( I I ) 1 x = 3 2 ⋅ 1 y 1 x + 1 y = 1 24
Đặt 1/x = u; 1/y = v,hệ (II)trở thành:
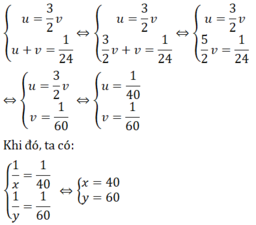
Vậy số ngày để đội A làm 1 mình xong đoạn đường đó là 40 ngày
Số ngày để đội B làm 1 mình xong đoạn đường đó là 60 ngày
Đúng 0
Bình luận (0)
Giải các hệ phương trình sau bằng cách đặt ẩn số phụ:
7
x
-
y
+
2
-
5
x
+
y
-...
Đọc tiếp
Giải các hệ phương trình sau bằng cách đặt ẩn số phụ: 7 x - y + 2 - 5 x + y - 1 = 4 , 5 3 x - y + 2 + 2 x + y - 1 = 4
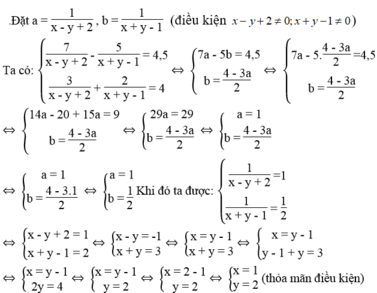
Vậy nghiệm của hệ phương trình là (x; y) = (1; 2).
Đúng 0
Bình luận (0)
Bằng cách đặt ẩn phụ (theo hướng dẫn), đưa các hệ phương trình sau về dạng hệ hai phương trình bậc nhất hai ẩn rồi giải:
1
x
-
2
+
1
y
-
1...
Đọc tiếp
Bằng cách đặt ẩn phụ (theo hướng dẫn), đưa các hệ phương trình sau về dạng hệ hai phương trình bậc nhất hai ẩn rồi giải: 1 x - 2 + 1 y - 1 = 2 2 x - 2 - 3 y - 1 = 1
Giair phương trình bằng cách đặt ẩn phụ:
a) \(x^2+2x\sqrt{x-\dfrac{1}{x}}=3x+1\)
b) \(x^2+\sqrt[3]{x^4-x^2}=2x+1\)
17 tháng 6 2021 lúc 16:41
Đề bài: giải hệ phương trình bằng phương pháp đặt ẩn phụ.
a. \(\left\{{}\begin{matrix}\dfrac{2x}{x+1}+\dfrac{y}{y+1}=2\\\dfrac{x}{x+1}+\dfrac{3y}{y+1}=-1\end{matrix}\right.\)
b. \(\left\{{}\begin{matrix}\dfrac{x+y}{xy}+\dfrac{xy}{x+y}=\dfrac{5}{2}\\\dfrac{x-y}{xy}+\dfrac{xy}{x-y}=\dfrac{10}{3}\end{matrix}\right.\)
Giúp mình với mình đang cần gấp
a) \(\left\{{}\begin{matrix}\dfrac{2x}{x+1}+\dfrac{y}{y+1}=2\\\dfrac{x}{x+1}+\dfrac{3y}{y+1}=-1\end{matrix}\right.\)(Đk: \(x\ne-1;y\ne-1\))
Đặt \(\dfrac{x}{x+1}\) là A
\(\dfrac{y}{y+1}\) là B
Ta có HPT mới : \(\left\{{}\begin{matrix}2A+B=2\\A+3B=-1\end{matrix}\right.\)(1)
Giải HPT (1) ta được A= \(\dfrac{7}{5}\) ; B=\(-\dfrac{4}{5}\)
+Với A=\(\dfrac{7}{5}\) ta có:
\(\dfrac{x}{x+1}=\dfrac{7}{5}\)
<=>\(5x=7x+7\)
<=>-2x=7
<=> x=\(-\dfrac{7}{2}\)
+Với B = \(-\dfrac{4}{5}\) ta có:
\(\dfrac{y}{y+1}=-\dfrac{4}{5}\)
<=>5y=-4y-4
<=>9y=-4
<=>y=\(-\dfrac{4}{9}\)
Vậy HPT có nghiệm (x;y) = \(\left\{-\dfrac{7}{2};-\dfrac{4}{9}\right\}\)
Đúng 1
Bình luận (0)
Bằng cách đặt ẩn phụ (theo hướng dẫn), đưa các hệ phương trình sau về dạng hệ hai phương trình bậc nhất hai ẩn rồi giải:
a)
1
x
−
1
y
1...
Đọc tiếp
Bằng cách đặt ẩn phụ (theo hướng dẫn), đưa các hệ phương trình sau về dạng hệ hai phương trình bậc nhất hai ẩn rồi giải:
a) 1 x − 1 y = 1 3 x + 4 y = 5 Đặt u = 1 x ; v = 1 y b) 1 x − 2 + 1 y − 1 = 2 2 x − 2 − 3 y − 1 = 1 đặt u = 1 x − 2 ; v = 1 y − 1
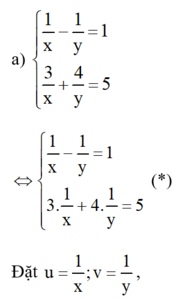
hệ phương trình (*) trở thành :
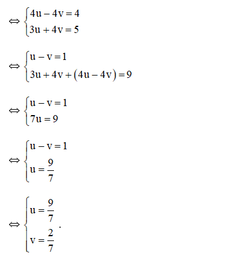
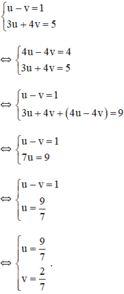
+ u = 9 7 ⇒ 1 x = 9 7 ⇒ x = 7 9 + v = 2 7 ⇒ 1 y − 2 7 ⇒ y − 7 2
Vậy hệ phương trình có nghiệm (7/9;7/2)
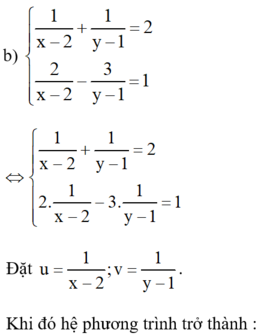
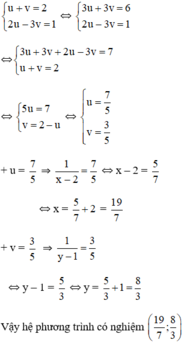
Kiến thức áp dụng
Giải hệ phương trình bằng phương pháp cộng đại số
1) Nhân hai vế của phương trình với mỗi hệ số thích hợp (nếu cần) sao cho hệ số của một trong hai ẩn bằng nhau hoặc đối nhau.
2) Áp dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
3) Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho và kết luận.
Đúng 0
Bình luận (0)