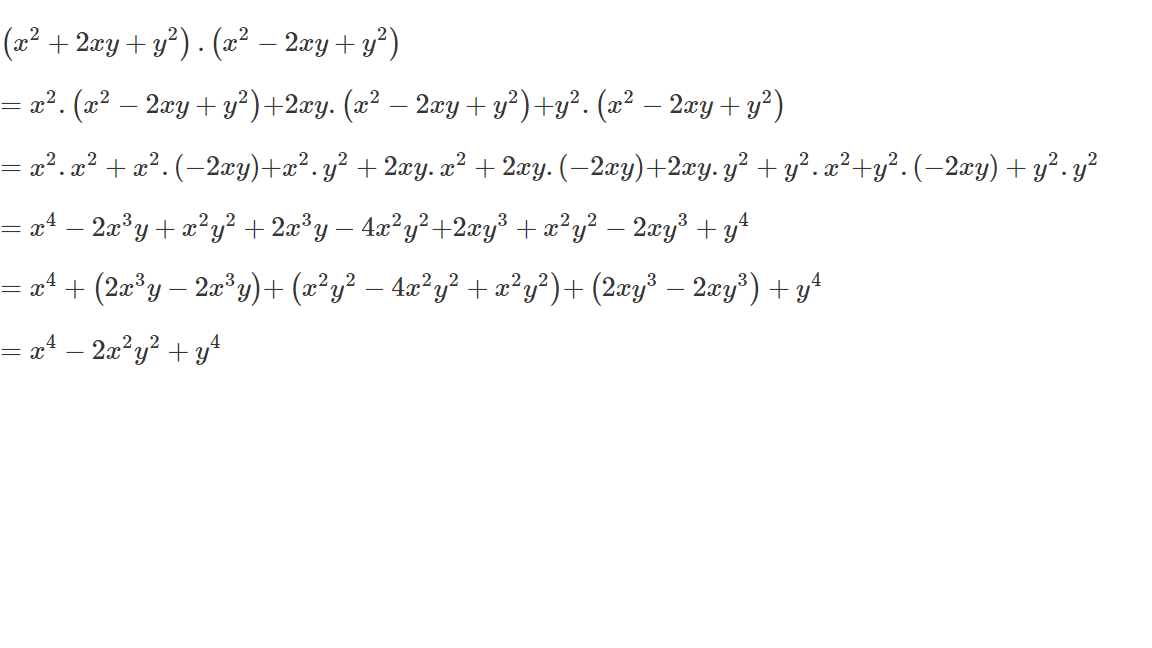x2 - 4x2y2 + y2 + 2xy

Những câu hỏi liên quan
1. Tìm min của biểu thức A = 4x4 + 4x2y2 + y2 +2
2. Tìm min của biểu thức B = x2 + 2xy +y2 + (y+1)2 + 12
\(1,Sửa:A=4x^4+4x^2y+y^2+2=\left(2x^2+y\right)^2+2\ge2\\ A_{min}=2\Leftrightarrow2x^2+y=0\Leftrightarrow x^2=-\dfrac{y}{2}\\ 2,B=\left(x+y\right)^2+\left(y+1\right)^2+12\ge12\\ B_{min}=12\Leftrightarrow\left\{{}\begin{matrix}x=-y=1\\y=-1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Phân tích đa thức thành nhân tử:
a) 3x-3y-x2+2xy-y2
b) x2-4x2y2+y2+2xy
c) (x+y)3-(x-y)3
d) x2-5x-14
\(a,=3\left(x-y\right)-\left(x-y\right)^2=\left(x-y\right)\left(3-x+y\right)\\ b,=\left(x+y\right)^2-4x^2y^2=\left(x-2xy+y\right)\left(x+2xy+y\right)\\ c,=\left(x+y-x+y\right)\left[\left(x+y\right)^2+\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\right]\\ =2y\left(x^2+2xy+y^2+x^2-y^2+x^2-2xy+y^2\right)\\ =2y\left(3x^2+y^2\right)\\ d,=x^2+2x-7x-14=\left(x+2\right)\left(x-7\right)\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
a) 3x-3y+x2-y2
b) (2xy+1)^2-(2x+y)^2
c)(x2+y2-5)^2-4(x2y2+4xy+4) d) (x2+y2-z2)^2-4x2y2
e) 9x2 +90
x+225-(x-7)^2
bn viết rõ đề đi bn
Vd:x2 là 2.x hay x\(^2\)
Có nhiều chỗ vậy lắm bn ạ,bn viết lại đề đi rồi tụi mk giúp cho.
Đúng 0
Bình luận (2)
a) \(3x-3y+x^2-y^2\)
\(=3\left(x-y\right)+\left(x+y\right)\left(x-y\right)\)
\(=\left(3+x+y\right)\left(x-y\right)\)
b) \(\left(2xy+1\right)^2-\left(2x+y\right)^2\)
\(=\left[\left(2xy+1\right)-\left(2x+y\right)\right]\left[\left(2xy+1\right)+\left(2x+y\right)\right]\)
\(=\left(2xy+1-2x-y\right)\left(2xy+1+2x+y\right)\)
\(=\left(y+1\right)\left(2x+1\right)\left(y-1\right)\left(2x-1\right)\)
c) \(\left(x^2+y^2-5\right)^2-4\left(x^2y^2+4xy+4\right)\)
↓
\(=\left(x^2-y^2-2y-1\right)\left(x^2-2xy+y^2-9\right)\)
\(=\left[x^2-\left(y^2+2y+1\right)\right]\left(x^2-2xy+y^2-9\right)\)
\(=\left[x^2-\left(y+1\right)^2\right]\left[\left(x-y\right)^2-3^2\right]\)
\(=\left[x^2-\left(-y-1\right)^2\right]\left(x-y+3\right)\left(x-y-3\right)\)
\(=\left(x+y+1\right)\left(x-y-1\right)\left(x-y+3\right)\left(x-y-3\right)\)
d) \(\left(x^2+y^2-z^2\right)^2-4x^2y^2\)
\(=\left(x^2+y^2-z^2\right)^2-\left(2xy\right)^2\)
\(=\left(x^2+y^2-z^2-2xy\right)\left(x^2+y^2-z^2+2xy\right)\)
\(=\left[\left(x-y\right)^2-z^2\right]\left[\left(x+y\right)^2-z^2\right]\)
\(=\left(x-y-z\right)\left(x-y+z\right)\left(x+y-z\right)\left(x+y+z\right)\)
e)
- \(9x^2+90=9\left(x+10\right)\)
- \(x+225-\left(x-7\right)^2\)
\(=x+225-\left(x^2-14x+49\right)\)
\(=x+225-x^2+14x-49\)
\(=-x^2+15x+176\)
\(=-\left(x^2-15x-176\right)\)
Đúng 0
Bình luận (1)
phân tích đa thức sau thành nhân tửx2 - 4x + 4 - y2x2 + 2xy + y2 - x- yx2 - 2xy + y2 - 92x3y + 2xy3 + 4x2y2 - 2xyx2+y2-2xy + 4x - 4yx3 - x + 3x2y + 3xy2 + y3 -yx2 - 2xy +y2 - 4z2x2 - x - y2 - yx2 - 2xy + y2 - z2
Đọc tiếp
phân tích đa thức sau thành nhân tử
x2 - 4x + 4 - y2
x2 + 2xy + y2 - x- y
x2 - 2xy + y2 - 9
2x3y + 2xy3 + 4x2y2 - 2xy
x2+y2-2xy + 4x - 4y
x3 - x + 3x2y + 3xy2 + y3 -y
x2 - 2xy +y2 - 4z2
x2 - x - y2 - y
x2 - 2xy + y2 - z2
`x^2 -4x+4-y^2`
`=(x^2 -4x+4)-y^2`
`=(x-2)^2 -y^2`
`=(x-2-y)(x-2+y)`
`x^2+2xy+y^2-x-y`
`=(x^2+2xy+y^2) -(x+y)`
`=(x+y)^2 -(x+y)`
`=(x+y)(x+y-1)`
`x^2-2xy+y^2-9`
`=(x^2-2xy+y^2)-3^2`
`=(x-y)^2-3^3`
`=(x-y-3)(x-y+3)`
Tách ra đi cậu.
Đúng 1
Bình luận (1)
Phân tích đa thức sau thành nhân tử: 4x2y2 – (x2 + y2)2
4x2y2 – (x2 + y2)2
= (2xy)2 – (x2 + y2)2
= (2xy + x2 + y2)(2xy - x2 - y2)
= - (x2 + 2xy + y2)(x2 - 2xy + y2)
= -(x + y)2 .(x - y)2
Đúng 0
Bình luận (0)
Cho hai số thực x, y thỏa mãn
x
2
-
y
2
+
1
2
+
4
x
2
y
2
-
x
2
-
y
2
0
. Gọi...
Đọc tiếp
Cho hai số thực x, y thỏa mãn x 2 - y 2 + 1 2 + 4 x 2 y 2 - x 2 - y 2 = 0 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P = x 2 + y 2 . Tính M + m
A. M + m = 3
B. M + m = 5
C. M + m = 2
D. M + m = 4
Thực hiện các phép tính sau:a)
y
4
x
2
−
2
xy
+
4
x
2
y
2
−
4
xy
với
x
≠
0
và
y
≠...
Đọc tiếp
Thực hiện các phép tính sau:
a) y 4 x 2 − 2 xy + 4 x 2 y 2 − 4 xy với x ≠ 0 và y ≠ 2 x ;
b) 1 1 − x + 1 1 + x + 2 1 + x 2 + 4 1 + x 4 + 8 1 + x 8 + 16 1 + x 16 với x ≠ ± 1 .
a,A=(x2+y2-2xy)+(-x2+y2+2xy)
A=x2+y2-2xy-x2+y2+2xy
=x2-x2+y2+y2+2xy-2xy
=y4
vậy da thức A sau khithu gọn là: y4
Đúng 0
Bình luận (2)
a,A=(x2+y2-2xy)+(-x2+y2+2xy)
= x2+y2-2xy+-x2+y2+2xy
=(x2-x2)+(y2+y2)+(-2xy+2xy)
= 2y2
Đúng 1
Bình luận (0)
Bài 2: Phân tích đa thức sau thành nhân tử
a) x2 + 2xy + y2 - 4
b) x2 - y2 + x + y
c) y2 + x2 + 2xy - 16
a) \(x^2+2xy+y^2-4=\left(x+y\right)^2-2^2\)
\(=\left(x+y-2\right)\left(x+y+2\right)\)
b) \(x^2-y^2+x+y=\left(x-y\right)\left(x+y\right)+1\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y+1\right)\)
c) \(y^2+x^2+2xy-16=x^2+2xy+y^2-16\)
\(=\left(x+y\right)^2-4^2=\left(x+y+4\right)\left(x+y-4\right)\)
Đúng 0
Bình luận (0)
tích của đa thức : x2+2xy+y2 với đa thức x2-2xy+y2
\(\left(x^2+2xy+y^2\right)\left(x^2-2xy+y^2\right)=\left(x-y\right)^2\cdot\left(x+y\right)^2=\left(x^2-y^2\right)^2=x^4-2x^2y^2+y^4\)
Đúng 2
Bình luận (0)
Ta có: (x2+2xy+y2)(x2-2xy+y2)
= (x+y)2(x-y)2=[(x+y)(x-y)]2
= (x2-y2)2=x4-2x2y2+y4
Đúng 1
Bình luận (0)