giá trị của tổng S= 20+22+24+ ....... +2016 là S= ...........
Những câu hỏi liên quan
giá trị tổng S=20+22+24+......+2016 là S
(cần gấp xog đầu tick nhé!)
- Số số hạng của dãy là: (2016-20):2+1=999(số)
Giá trị tổng S là : ( 2016 + 20 ).999:2=1016982
Đ/s
Đúng 0
Bình luận (0)
giá trị tổng S= 20+22+24+...+2016
để bạn chờ lâu. Kết quả là 999 đó bạn
Đúng 0
Bình luận (0)
giá trị tổng S= 20+22+24+...+2016
Giá trị của tổng \(S=20+22+24+....+2016\)là \(S=\).....................
SSH của S là : ( 2016 - 20 ) : 2 + 1 = 999 ( số hạng )
<=> S = ( 2016 + 20 ) . 999 : 2 = 1016982
Vậy S = 1016982
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tổng của S = 20+22+24+...+2016 là S =?
Số các số hạng của tổng S là: (2016 - 20):2+1=999 (số)
Tổng của S là: (2016+20)*999:2=1016982
Đúng 0
Bình luận (0)
Câu 1.1: Số nguyên tố p sao cho p2 + 44 là số nguyên tố là p =.........
Câu 1.2: Giá trị của tổng S = 20 + 22 + 24 + ....... + 2016 là S = ..............
Giúp mình với
Mình giải nè:
Bài 1.1:
p2 + 44
-) Với p = 2 => p2 + 44 = 22 + 44 = 4 + 44 = 48 là hợp số.
=> p = 2 (loại)
-) Với p = 3 => p2 + 44 = 32 + 44 = 9 + 44 = 53 là số nguyên tố
-) Với p > 3 => p có dạng 3k + 1 và 3k + 2
+) p = 3k + 1 = > p2 + 44 = (3k + 1)2 + 44
= (3k)2 + 2 . 3k . 1 + 12 + 44
= 9k . k2 + 6k + 1 + 44
= 9k . k2 + 6k + 45
= 3 . (3 . k2 + 2k + 15)
Vì 3 \(⋮\)3 nên 3 . (3. k2 + 2k + 15) \(⋮\)3 (là hợp số)
=> p = 3k + 1 (loại)
+) p = 3k + 2 => p2 + 44 = (3k + 2)2 + 44
= (3k)2 + 2 . 3k . 2 + 22 + 44
= 9 . k2 + 12 . k + 4 + 44
= 9 . k2 + 12 . k + 48
= 3. (2 . k2 + 4 . k + 16)
Vì 3 \(⋮\)3 nên 3 . (2 . k2 + 4 . k + 16) \(⋮\)3 (là hợp số)
=> p = 3k + 2 (loại)
=> p = 3
Vậy p = 3 thì p2 + 44 là số nguyên tố.
Bài 1.2:
Giải:
S = 20 + 22 + 24 + ... + 2016
Số số hạng của tổng S là:
(2016 - 20 ) : 2 + 1 = 999 (số hạng)
Giá trị của tổng S là:
(20 + 2016) . 999 : 2 = 1016982
Vậy S = 20 + 22 + 24 + ... + 2016 có giá trị là 1016982.
Chúc bạn học tốt!
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
x
-
2
2
+
y
-
2
2
+
z
-
2
2
4
và đường thẳng
∆
:...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : x - 2 2 + y - 2 2 + z - 2 2 = 4 và đường thẳng ∆ : x = 1 + m t y = m 2 - m t z = - m 2 t Gọi (P), (Q) là hai mặt phẳng phân biệt cùng chứa đường thẳng ∆ và tiếp xúc với mặt cầu (S) tại các điểm A và B. Tổng giá trị lớn nhất và giá trị nhỏ nhất của AB bằng
A. 4 13 + 4 5 3
B. 4 13 + 4 5 5
C. 20 13 + 12 5 15
D. 12 13 + 20 5 15
Có
∆
:
x
=
1
+
m
t
y
=
m
2
-
m
t
z
=
-
m
2
t
:x+y+z-1=0
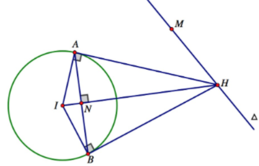
Mặt cầu (S) có tâm I(2;2;2), R = 2 và đường thẳng ∆ luôn đi qua điểm cố định M(1;0;0).
Gọi H = ∆ ∩ ( I A B ) ta có
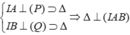
Gọi 
là trung điểm của AB và 
Theo hệ thức lượng cho tam giác vuông IAH có 
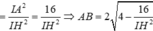
Ta có 
Chọn đáp án D.
Đúng 0
Bình luận (0)
Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số
y
1
4
x
4
-
19
2
x
2
+...
Đọc tiếp
Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số y = 1 4 x 4 - 19 2 x 2 + 30 x + m - 20 trên đoạn [0;2] không vượt quá 20. Tổng các phần tử của S bằng
A.210
B.-195
C.105
D.300
Chọn C
Xét hàm số 
trên đoạn 
Ta có 
; 
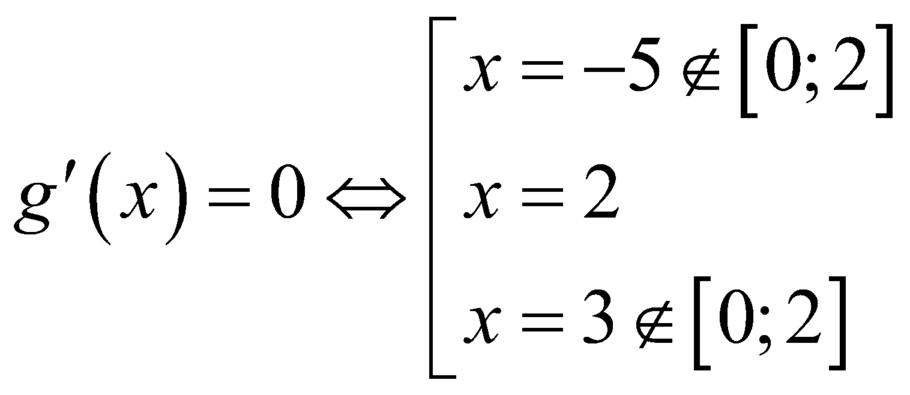
Bảng biến thiên
; 
.
Để 
thì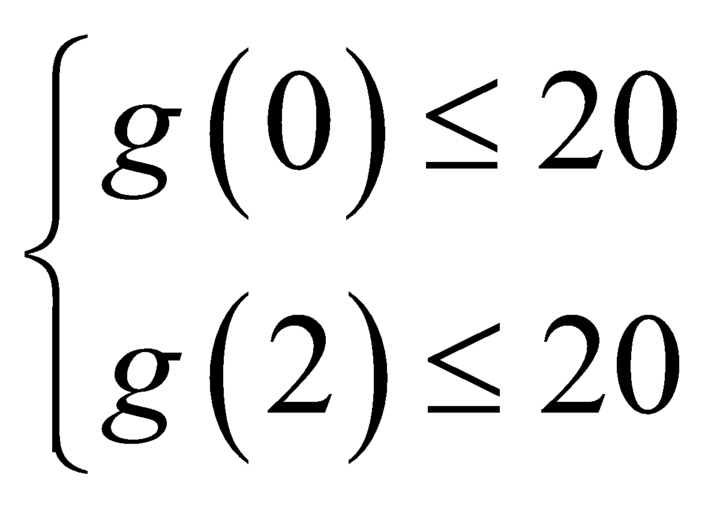 
.
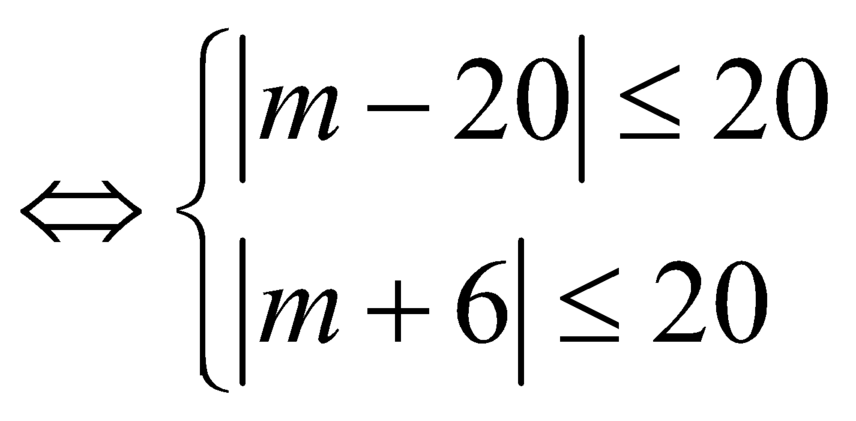
Mà 
nên 
.
Vậy tổng các phần tử của 
là 
.
Đúng 0
Bình luận (0)
Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số y
1
4
x
4
-
19
2
x
2
+
30
x
+
m
-
20...
Đọc tiếp
Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số y = 1 4 x 4 - 19 2 x 2 + 30 x + m - 20 trên đoạn [0;2] không vượt quá 20. Tổng các phần tử của S bằng
A. 210
B. -195
C. 105
D. 300
Chọn C
Xét hàm số 
trên đoạn [0;2]
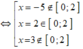
Bảng biến thiên:
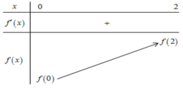
với f(0) = m - 20; f(2) = m + 6
Xét hàm số y = 1 4 x 4 - 19 2 x 2 + 30 x + m - 20 trên đoạn [0;2]
+ Trường hợp 1: 
Ta có:
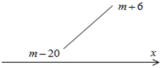
suy ra không có giá trị m.
+ Trường hợp 2: 
Ta có:
Vì m nguyên nên 
+ Trường hợp 3: 
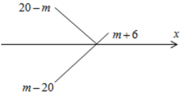
Vì m nguyên nên 
Vậy 
Tổng các phần tử của S bằng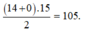 
Đúng 0
Bình luận (0)