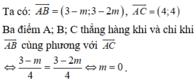Bài 1:
Để A giao B bằng rỗng thì \(\left[{}\begin{matrix}m+3< -3\\2m-1>6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m< -6\\m>\dfrac{7}{2}\end{matrix}\right.\)

Để A giao B khác rỗng thì \(\left[{}\begin{matrix}m+1< 2m\\m+3>2m-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-m< -1\\-m>-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m>1\\m< 4\end{matrix}\right.\)

Vậy: Có 2 giá trị nguyên thỏa mãn

A giao B như thế nào với rỗng vậy bạn?

Để tìm sao cho A giao B bằng rỗng, ta cần tìm điều kiện để đoạn thẳng AB không cắt nhau. Điều này có thể xảy ra trong các trường hợp sau: a) Trong trường hợp này, A=(-6,20) và B=(5,3m+7). Để đoạn thẳng AB không cắt nhau, ta cần xảy ra ít nhất một trong hai trường hợp sau: - Điểm A nằm dưới đường thẳng AB, tức là tọa độ y của A lớn hơn tọa độ y của B: 20 ​​> 3m+7 . - Điểm A nằm trên đường thẳng AB, tức là tọa độ y của A bằng tọa độ y của B: 20 ​​= 3m+7. b) Trong trường hợp này, A=(10,40] và B=(7,2m-3). Tương tự như trường hợp a), ta cần ít nhất một trong hai trường hợp sau: - Điểm A nằm dưới đường thẳng AB: 40 > 2m-3. - Điểm A nằm trên đường thẳng AB: 40 = 2m-3. c) Trong trường hợp này, A=(-âm vô cực,9] và B=[m,2m-1). Điều kiện để đoạn thẳng AB không cắt nhau là điểm A nằm trên hoặc dưới đường thẳng AB. Điều này xảy ra khi tọa độ y của điểm A lớn hơn hoặc bằng tọa độ y của điểm B: 9 ≥ 2m-1. d) Trong trường hợp này, A=(-âm vô cực,2m-3) và B=(m+9,+dương vô cực). Điều kiện để đoạn thẳng AB không cắt nhau là điểm A nằm trên hoặc dưới đường thẳng AB. Điều này xảy ra khi tọa độ y của điểm A lớn hơn hoặc bằng tọa độ y của điểm B: 2m-3 ≥ +dương vô cực. e) Trong trường hợp này, A=(-âm vô cực,6m) và B=(18,2m-1). Điều kiện để đoạn thẳng AB không cắt nhau là điểm A nằm trên hoặc dưới đường thẳng AB. Điều này xảy ra khi tọa độ y của điểm A lớn hơn hoặc bằng tọa độ y của điểm B: 6m ≥ 2m-1. Vì vậy, để tìm sao cho A giao B bằng rỗng, bạn cần giải các phương trình và bất đẳng thức trên mỗi trường hợp. Mỗi trường hợp sẽ đưa ra một công thức hoặc một khoảng giá trị của m.

Chọn C

Vecto AB = (3 - m; 3 - 2m)
Vecto AC = (-2; 2)
A, B, C thẳng hàng
<=> vecto AB và vecto AC cùng phương
<=> (3 - m)/(-2) = (3 - 2m)/2
<=> m - 3 = 3 - 2m
<=> 3m = 6
=> m = 2

-> A

Đáp án: D

Điều kiện để tồn tại tập hợp A, B là

m - 1 < 4 - 2 < 2 m + 2 ⇔ m < 5 m > - 2 ⇔ - 2 < m < 5 A ∩ B ⊂ ( - 1 ; 3 ) ⇔ m - 1 ≥ - 1 2 m + 2 ≤ 3 ⇔ m ≥ 0 m ≤ 1 2 ⇔ 0 ≤ m ≤ 1 2

Kết hợp với điều kiện (*) ta có 0 ≤ m ≤ 1/2 là giá trị cần tìm.

Bàu này quá dễ cái này lớp 6 còn còn có trong chương trình :)

Cho hai tập khác rỗng : A = (m – 1; 4], B = (-2; 2m + 2), với m ∈ Rℝ. Giá trị m để A  ∩ B ⊂ (-1; 3) là:

Điều kiện để tồn tại tập hợp A, B là

{m−1<4−2<2m+2⇔{m<5m>−2⇔−2<m<5A∩B⊂(−1;3)⇔{m−1≥−12m+2≤3⇔{m≥0m≤12⇔0≤m≤12m-1<4-2<2m+2⇔m<5m>-2⇔-2<m<5A∩B⊂(-1;3)⇔m-1≥-12m+2≤3⇔m≥0m≤12⇔0≤m≤12

Kết hợp với điều kiện (*) ta có 0 ≤ m ≤ 1/2 là giá trị cần tìm.

Cách này là tôi tự làm trong 1 lần ở Viet Jack kiểu tham khảo chứ k^o coppy mạng :)

>3.....@Chi

Điều kiện để tồn tại tập hợp A, B là

\(\hept{\begin{cases}m-1>4\\-2< 2m+2\end{cases}}\Rightarrow\hept{\begin{cases}m< 5\\m>-2\end{cases}}\Leftrightarrow-2< m< 5\)

A ∩ B ⊂ (-1; 3) \(\Leftrightarrow\hept{\begin{cases}m-1\ge-1\\2m+2\le3\end{cases}}\Leftrightarrow\hept{\begin{cases}m\ge0\\m\le\frac{1}{2}\end{cases}}\Leftrightarrow0\le m\le\frac{1}{2}\)

$\begin{array}{c}m-1<4\\ -2<2m+2\end{array}\iff \{\begin{array}{c}m<5\\ m>-2\end{array}\iff -2<m<5A\cap B\subset (-1;3)\iff \{\begin{array}{c}m-1\ge -1\\ 2m+2\le 3\end{array}\iff \{\begin{array}{c}m\ge 0\\ m\le \frac{1}{2}\end{array}\iff 0\le m\le \frac{1}{2}$

Kết hợp với điều kiện (*) ta có 0 ≤ m ≤ 1/2 là giá trị cần tìm.

Đáp án B