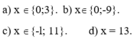1: Để A>0 thì x-1<0

hay x<1

Kết hợp ĐKXĐ, ta được: \(0\le x< 1\)

1) Để A > 0 thì:

\(x-1< 0\Leftrightarrow x< 1\)

\(\Rightarrow0\le x< 1\) và \(x\ne1\)

2) \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=1+\dfrac{2}{\sqrt{x}-1}\)

Để A<1 thì \(\dfrac{2}{\sqrt{x}-1}< 0\)

\(\Rightarrow\sqrt{x}-1< 0\Leftrightarrow\sqrt{x}< 1\)

Mà x\(\ge0,x\ne1\)

\(\Rightarrow0\le x< 1\)

Bài 2: 

Để A<1 thì A-1<0

\(\Leftrightarrow\dfrac{\sqrt{x}+1-\sqrt{x}+1}{\sqrt{x}-1}< 0\)

\(\Leftrightarrow\dfrac{2}{\sqrt{x}-1}< 0\)

\(\Leftrightarrow\sqrt{x}-1< 0\)

hay x<1

Kết hợp ĐKXĐ, ta được: \(0\le x< 1\)

d. Áp dụng BĐT Caushy Schwartz ta có:

\(x+y+\dfrac{1}{x}+\dfrac{1}{y}\le x+y+\dfrac{\left(1+1\right)^2}{x+y}=x+y+\dfrac{4}{x+y}\le1+\dfrac{4}{1}=5\)

-Dấu bằng xảy ra \(\Leftrightarrow x=y=\dfrac{1}{2}\)

c. Bạn kiểm tra lại đề nhé.

b. \(5x\left(2-x\right)=-5x\left(x-2\right)=-5\left(x^2-2x\right)=-5\left(x^2-2x+1-1\right)=-5\left(x-1\right)^2+5\le5\)-Dấu bằng xảy ra \(\Leftrightarrow x=1\)

a.

\(\left(80-2x\right)\left(50-2x\right)x=\dfrac{2}{3}\left(40-x\right)\left(50-2x\right)3x\le\dfrac{2}{3}\left(\dfrac{40-x+50-2x+3x}{3}\right)^3=18000\)

Dấu "=" xảy ra khi \(40-x=50-2x=3x\Leftrightarrow x=10\)

b.

\(5x\left(2-x\right)=5.x\left(2-x\right)\le\dfrac{5}{4}\left(x+2-x\right)^2=5\)

Dấu "=" xảy ra khi \(x=2-x\Rightarrow x=1\)

c.

Biểu thức này chỉ có min, ko có max

d.

\(x+y\le1\Rightarrow-\left(x+y\right)\ge-1\)

\(x+y+\dfrac{1}{x}+\dfrac{1}{y}=\left(4x+\dfrac{1}{x}\right)+\left(4y+\dfrac{1}{y}\right)-3\left(x+y\right)\ge2\sqrt{\dfrac{4x}{x}}+2\sqrt{\dfrac{4y}{y}}-3.1=5\)

Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)

9.

\(A>1\Leftrightarrow\dfrac{\sqrt{x}-2}{\sqrt{x}-1}>1\)

\(\Leftrightarrow\dfrac{\sqrt{x}-2}{\sqrt{x}-1}-1>0\)

\(\Leftrightarrow\dfrac{\sqrt{x}-2-\sqrt{x}+1}{\sqrt{x}-1}>0\)

\(\Leftrightarrow\dfrac{-1}{\sqrt{x}-1}>0\)

\(\Leftrightarrow\sqrt{x}-1< 0\)

\(\Leftrightarrow x< 1\)

Kết hợp với điều kiện giả thiết.

10.

\(P< 1\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-1}< 1\)

\(\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-1< 0\)

\(\Leftrightarrow\dfrac{\sqrt{x}+1-\sqrt{x}+1}{\sqrt{x}-1}< 0\)

\(\Leftrightarrow\dfrac{2}{\sqrt{x}-1}< 0\)

\(\Leftrightarrow\sqrt{x}-1< 0\)

\(\Leftrightarrow x< 1\)

Kết hợp với điều kiện giả thiết.

Bài 9:

Để A>1 thì A-1>0

\(\Leftrightarrow\dfrac{\sqrt{x}-2-\sqrt{x}+1}{\sqrt{x}-1}>0\)

\(\Leftrightarrow\dfrac{-1}{\sqrt{x}-1}>0\)

\(\Leftrightarrow\sqrt{x}-1< 0\)

hay x<1

Kết hợp ĐKXĐ, ta được: \(0\le x< 1\)

Bài 10:

Để P<1 thì P-1<0

\(\Leftrightarrow\dfrac{\sqrt{x}+1-\sqrt{x}+1}{\sqrt{x}-1}< 0\)

\(\Leftrightarrow\dfrac{2}{\sqrt{x}-1}< 0\)

\(\Leftrightarrow\sqrt{x}-1< 0\)

hay x<1

Kết hợp ĐKXĐ, ta được: \(0\le x< 1\)

8: Để \(P< \dfrac{1}{4}\) thì \(P-\dfrac{1}{4}< 0\)

\(\Leftrightarrow\dfrac{4\sqrt{x}-8-\sqrt{x}-1}{\sqrt{x}+1}< 0\)

\(\Leftrightarrow3\sqrt{x}< 9\)

hay x<9

Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0\le x< 9\\x\ne1\end{matrix}\right.\)

7.

\(P< 1\Leftrightarrow\dfrac{x+\sqrt{x}}{\sqrt{x}-1}< 1\)

\(\Leftrightarrow\dfrac{x+\sqrt{x}}{\sqrt{x}-1}-1< 0\)

\(\Leftrightarrow\dfrac{x+\sqrt{x}-\sqrt{x}+1}{\sqrt{x}-1}< 0\)

\(\Leftrightarrow\dfrac{x+1}{\sqrt{x}-1}< 0\)

\(\Leftrightarrow\sqrt{x}-1< 0\)

\(\Leftrightarrow x< 1\)

Vậy \(0\le x< 1\)

8.

\(P< \dfrac{1}{4}\Leftrightarrow\dfrac{\sqrt{x}-2}{\sqrt{x}+1}< \dfrac{1}{4}\)

\(\Leftrightarrow4\left(\sqrt{x}-2\right)< \sqrt{x}+1\)

\(\Leftrightarrow4\sqrt{x}-8< \sqrt{x}+1\)

\(\Leftrightarrow3\sqrt{x}< 9\)

\(\Leftrightarrow x< 9\)

Vậy \(0\le x< 9;x\ne1\)

a) x Î{0;3}.

b) xÎ{0;-9}.

c) x Î{-l; 11}.

d) x = 13.

a) 4x(x+1)=8(x+1)

<=>4x(x+1)-8(x+1)=0

<=>(4x-8)(x+1)=0

<=>\(\left[\begin{array}{} 4x-8=0\\ x+1=0 \end{array} \right.\)

<=>\(\left[\begin{array}{} x=2\\ x=-1 \end{array} \right.\)

Vậy...

b)x(x-1)-2(1-x)=0

<=>(x+2)(x-1)=0

<=>\(\left[\begin{array}{} x+2=0\\ x-1=0 \end{array} \right.\)

<=>\(\left[\begin{array}{} x=-2\\ x=1 \end{array} \right.\)

Vậy...

c)5x(x-2)-(2-x)=0

<=>(5x+1)(x-2)=0

<=>\(\left[\begin{array}{} 5x+1=0\\ x-2 \end{array} \right.\)

<=>\(\left[\begin{array}{} x=-1/5\\ x=2 \end{array} \right.\)

d)5x(x-200)-x+200=0

<=>(5x-1)(x-200)=0

<=>\(\left[\begin{array}{} 5x-1=0\\ x-200=0 \end{array} \right.\)

<=>\(\left[\begin{array}{} x=1/5\\ x=200 \end{array} \right.\)

e)\(x^3+4x=0 \)

\(\Leftrightarrow x(x^2+4)=0 \)

\(\Leftrightarrow \left[\begin{array}{} x=0\\ x^2+4=0 (loại vì x^2+4>=0 với mọi x) \end{array} \right.\)

Vậy x=0

f)\((x+1)=(x+1)^2\)

\(\Leftrightarrow (x+1)-(x+1)^2=0\)

\(\Leftrightarrow (x+1)(1-x-1)=0\)

\(\Leftrightarrow (x+1)(-x)=0\)

\(\Leftrightarrow \left[\begin{array}{} x=-1\\ x=0 \end{array} \right.\)

Vậy....