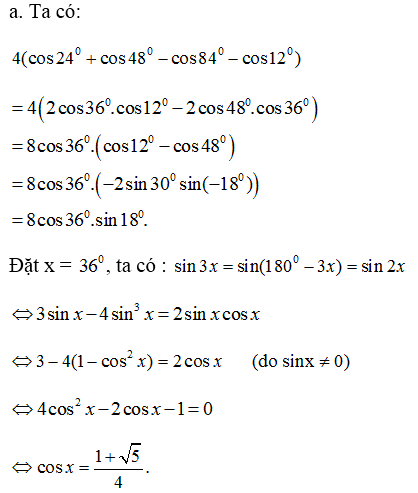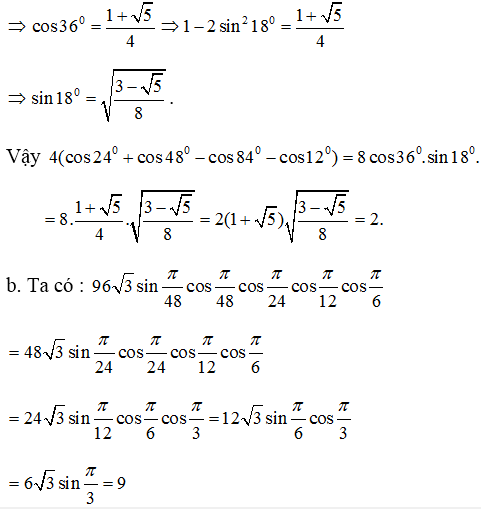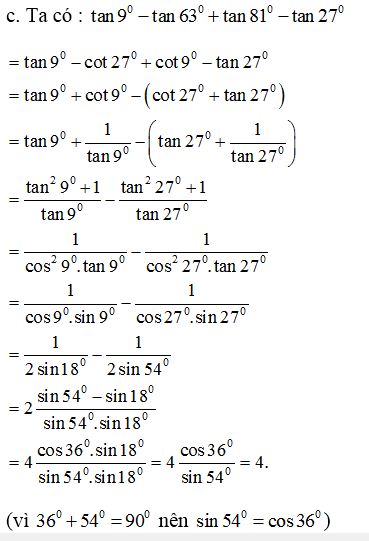tan27. tan42 . tan48 . tan63

Những câu hỏi liên quan
Rút gọn B = tan9° - tan27° - tan63° + tan81°
tính
A=sin10+sin40-cos50-cos80
B=cos15+cos35-sin65-sin75
C=\(\dfrac{tan27.tan63}{cot63.cot27}\)
D= \(\dfrac{cot20.cot45.cot70}{tan20.tan45.tan70}\)
Giải:
\(A=\sin10+\sin40-\cos50-\cos80\)
\(\Leftrightarrow A=\cos80+\cos50-\cos50-\cos80\)
\(\Leftrightarrow A=0\)
Vậy ...
\(B=\cos15+\cos25-\sin65-\sin75\)
\(\Leftrightarrow B=\sin75+\sin65-\sin65-\sin75\)
\(\Leftrightarrow B=0\)
Vậy ...
\(C=\dfrac{\tan27.\tan63}{\cot63.\cot27}\)
\(\Leftrightarrow C=\dfrac{\tan27.\tan63}{\tan27.\tan63}\)
\(\Leftrightarrow C=1\)
Vậy ...
\(D=\dfrac{\cot20.\cot45.\cot70}{\tan20.\tan45.\tan70}\)
\(\Leftrightarrow D=\dfrac{\cot20.\cot45.\cot70}{\cot70.\cot45.\cot20}\)
\(\Leftrightarrow D=1\)
Vậy ...
Đúng 0
Bình luận (0)
bài 1 tính giá trị biểu thức sau
A = sin 10 + sin 40 - cos 55 - cos 80
B = cos 15 + cos 35 - sin 55 - sin 75
C = \(\frac{tan27^0.tan63^0}{cot63^0.cot27^0}\)
D = \(\frac{cot20^0cot45^0cot70^0}{tan20^0tan45^0tan70^0}\)
Tính :
a) \(4\left(\cos24^0+\cos48^0-\cos84^0-\cos12^0\right)\)
b) \(96\sqrt{3}\sin\dfrac{\pi}{48}\cos\dfrac{\pi}{48}\cos\dfrac{\pi}{24}\cos\dfrac{\pi}{12}\cos\dfrac{\pi}{6}\)
c) \(\tan9^0-\tan63^0+\tan81^0-\tan27^0\)
1;tính A dfrac{1}{cos290^o}+dfrac{1}{sqrt{3}sin250^o}
2; tính B (1+tan 20o) ( 1+tan25o)
3; tính tan9o-tan27o-tan63o+ tan81o
4; tính D sin^2dfrac{pi}{9}+sin^2dfrac{2pi}{9}+sindfrac{pi}{9}sindfrac{2pi}{9}
5; tính E; sindfrac{pi}{32}cosdfrac{pi}{32}cosdfrac{pi}{16}cosdfrac{pi}{8}
Đọc tiếp
1;tính A= \(\dfrac{1}{\cos290^o}+\dfrac{1}{\sqrt{3}\sin250^o}\)
2; tính B = (1+tan 20o) ( 1+tan25o)
3; tính tan9o-tan27o-tan63o+ tan81o
4; tính D= \(\sin^2\dfrac{\pi}{9}+\sin^2\dfrac{2\pi}{9}+\sin\dfrac{\pi}{9}\sin\dfrac{2\pi}{9}\)
5; tính E;= \(\sin\dfrac{\pi}{32}\cos\dfrac{\pi}{32}\cos\dfrac{\pi}{16}\cos\dfrac{\pi}{8}\)
So sánh: Cos42 và Tan42
\(\cos42\approx0,743\)
\(\tan42\approx0,900\)
Vậy: Tan42 > Cos42
Đúng 0
Bình luận (0)
Tan69°–cot21°+cot27°/tan63°
\(\dfrac{sin48^o}{cos42^o}-cos60^o+tan27^o.tan63^o+sin30^o\)
\(=\dfrac{\sin48^0}{\sin48^0}-\sin30^0+\tan27^0\cdot\cot27^0+\sin30^0=1+1=2\)
Đúng 2
Bình luận (0)
Sắp xếp các tỉ số lượng giác sau theo thứ tự từ lớn đến bé: a) tan42*, cot71*, tan38*, cot69*15’, tan28* b) sin32*, cos51* , sin39* , cos79*13, sin38*
cot710 = tan190; cot690 = tan = 210
=> tan190 < tan210 < tan280 < tan390 < tan420
=> cot710 < cot690 < tan280 < tan390 < tan420
Đúng 0
Bình luận (1)
\(a,\cot71^0=\tan19^0< \cos69^015'=\tan20^045'< \tan28^0< \tan38^0< \tan42^0\\ b,\cos79^013'=\sin10^047'< \sin32^0< \sin38^0< \cos51^0=\sin39^0\)
Đúng 1
Bình luận (0)
cos510 = sin390
cos79013' = sin10047'
⇒ cos79013' < sin320 < sin380 < cos510 = sin390
Đúng 0
Bình luận (0)
Câu 1. Không dùng máy tinh,tính giá trị biểu thức:
a/ \(A=sin^234^o+\dfrac{tan48^o}{cot42^o}+sin^256^o\)
b/ B=\(cos^213^o+\dfrac{3tan26^o}{cot64^o}+cos^277^o+2cot32^o.cot58^o\)
c/\(B=\dfrac{5tan55^o}{cot35^o}-2sin^261^o-2sin^229^o\)
\(a,A=\sin^234^0+\cos^234^0+\dfrac{\cot42^0}{\cot42^0}=1+1=2\\ b,B=\left(\cos^213^0+\sin^277^0\right)+\dfrac{3\cot64^0}{\cot64^0}+2\cot32^0\cdot\tan32^0\\ B=1+3+2\cdot1=6\\ c,B=\dfrac{5\cot35^0}{\cot35^0}-2\left(\sin^261^0-\cos^261^0\right)=5-2\cdot1=3\)
Đúng 2
Bình luận (0)