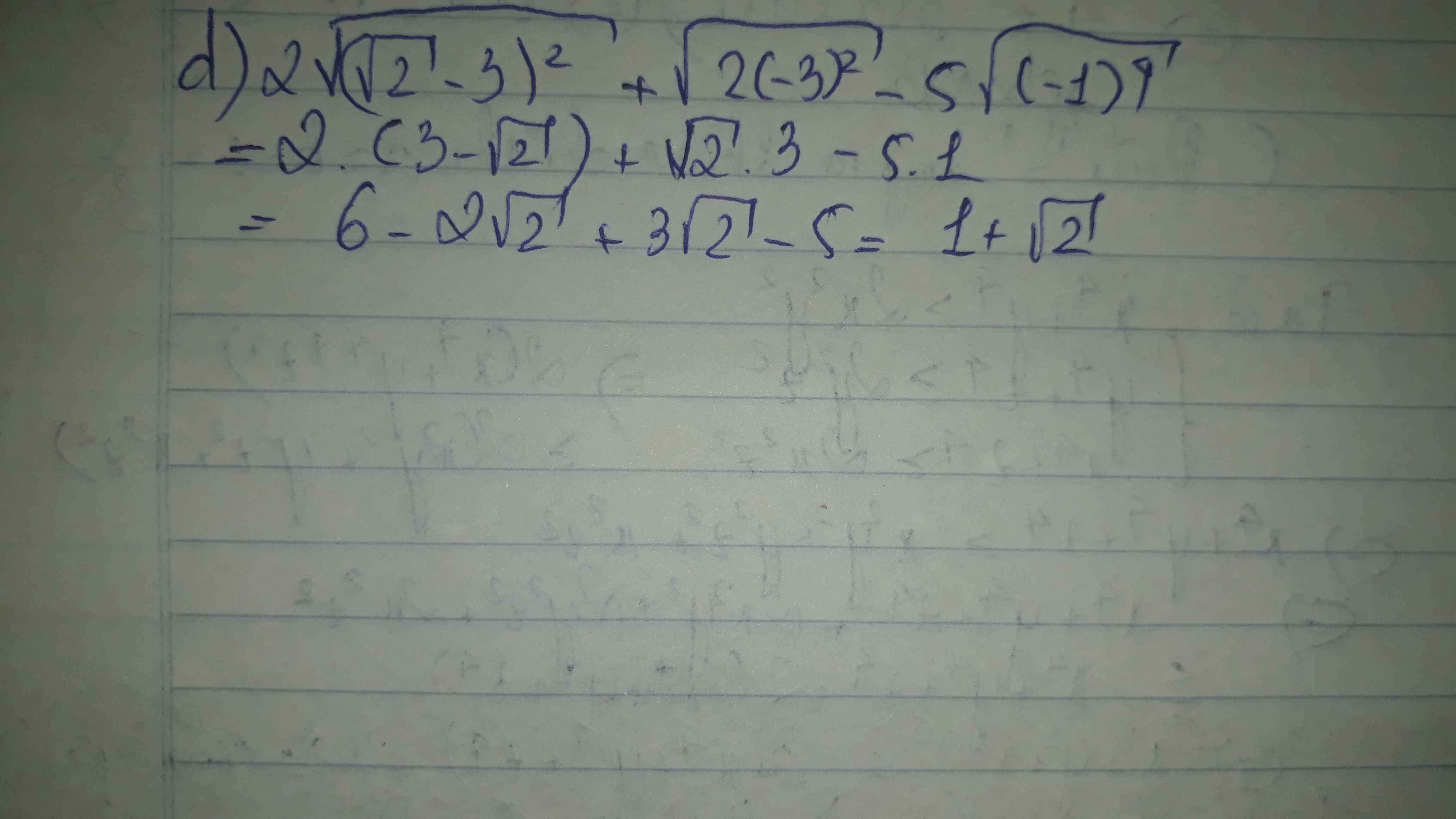Rút gọn \(\left(2+3\sqrt{2}\right)^2-\sqrt{288}\)

Những câu hỏi liên quan
Rút gọn:
\(\sqrt{\left(3-2\sqrt{2}\right)^2}\) + \(\sqrt{\left(3+2\sqrt{2}\right)^2}\)
`\sqrt{(3-2\sqrt{2})^2}+\sqrt{(3+2\sqrt{2})^2}`
`=|3-2\sqrt{2}|+3+2\sqrt{2}`
`=3-2\sqrt{2}+3+2\sqrt{2}=6`
Đúng 1
Bình luận (0)
rút gọn M=\(\left(\sqrt{6}+\sqrt{2}\right)\left(\sqrt{3}-2\right)\sqrt{\sqrt{3}+2}\)
\(M=\left(\sqrt{6}+\sqrt{2}\right)\left(\sqrt{3}-2\right)\sqrt{\sqrt{3}+2}\)
\(=\left(\sqrt{3}+1\right).\sqrt{2}.\sqrt{\sqrt{3}-2}.\sqrt{\sqrt{3}-2}.\sqrt{\sqrt{3}+2}\)
\(=\left(\sqrt{3}+1\right)\sqrt{4-2\sqrt{3}}\sqrt{\left(\sqrt{3}-2\right)\left(\sqrt{3}+2\right)}\)
\(=\left(\sqrt{3}+1\right)\sqrt{\left(\sqrt{3}-1\right)^2}.\left(-1\right)=\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right).\left(-1\right)=-2\)
Đúng 2
Bình luận (0)
Rút gọn biểu thức:
\(A=\sqrt{\left(2-\sqrt{7}\right)^2}+\left(\sqrt{7}-1\right)^2\)
\(B=3\sqrt{\left(1,5\right)^2}-4\sqrt{\left(3-\sqrt{2}\right)^2}\)
\(A=\left|2-\sqrt{7}\right|+7-2\sqrt{7}+1\)
\(=\sqrt{7}-2+8-2\sqrt{7}\) \(=6-\sqrt{7}\)
\(B=3\cdot1,5-4\cdot\left|3-\sqrt{2}\right|\) \(=4,5-4\left(3-\sqrt{2}\right)\)
\(=4,5-12+4\sqrt{2}\) \(=4\sqrt{2}-7,5\)
Đúng 0
Bình luận (0)
Ta có: \(A=\sqrt{\left(2-\sqrt{7}\right)^2}+\left(\sqrt{7}-1\right)^2\)
\(=\sqrt{7}-2+8-2\sqrt{7}\)
\(=6-\sqrt{7}\)
Đúng 0
Bình luận (0)
Rút gọn \(\left(2+\sqrt{3}-\sqrt{2}\right)\left(2-\sqrt{3}-\sqrt{2}\right)\left(3+2\sqrt{2}\right)\sqrt{3-2\sqrt{2}}\)
Ta xét:
\(a=\left(2+\sqrt{3}-\sqrt{2}\right)\left(2-\sqrt{3}-\sqrt{2}\right)\)
\(a=\left(2-\sqrt{2}\right)^2-\left(\sqrt{3}\right)^2\)
\(a=6-4\sqrt{2}-3\)
\(a=3-4\sqrt{2}\)
và
\(b=\left(3+2\sqrt{2}\right)\sqrt{3-2\sqrt{2}}\)
\(b=\sqrt{3+2\sqrt{2}}\cdot\left(\sqrt{3+2\sqrt{2}}\cdot\sqrt{3-2\sqrt{2}}\right)\)
\(b=\sqrt{3+2\sqrt{2}}\cdot\sqrt{3^2-\left(2\sqrt{2}\right)^2}\)
\(b=\sqrt{3+2\sqrt{2}}\cdot\sqrt{9-8}\)
\(b=\sqrt{3+2\sqrt{2}}\)
=> \(ab=\left(3-4\sqrt{2}\right)\sqrt{3+2\sqrt{2}}\)
Rút gọn các biểu thức sau:
d) \(2\sqrt{\left(\sqrt{2}-3\right)^2}+\sqrt{2\left(-3\right)^2}-5\sqrt{\left(-1\right)^4}\)
\(=2\left|3-\sqrt{2}\right|+\sqrt{18}-5.1=6-2\sqrt{2}+3\sqrt{2}-5\)
\(=1+\sqrt{2}\)
Đúng 1
Bình luận (0)
rút gọn biểu thức chưa căn thức bậc hai:
1,sqrt{left(1-sqrt{2}right)^2}+sqrt{left(sqrt{2}+3right)^2}
2, sqrt{left(sqrt{3}-2right)^2}+sqrt{left(sqrt{3}-1right)^2}
3,sqrt{left(sqrt{5}-3right)^2}+sqrt{left(sqrt{5}-2right)^2}
4,sqrt{left(3+sqrt{2}right)^2}+sqrt{left(3-sqrt{2}right)^2}
5,sqrt{left(2-sqrt{3}right)^2}-sqrt{left(2+sqrt{3}right)^2}
Đọc tiếp
rút gọn biểu thức chưa căn thức bậc hai:
1,\(\sqrt{\left(1-\sqrt{2}\right)^2}+\sqrt{\left(\sqrt{2}+3\right)^2}\)
2, \(\sqrt{\left(\sqrt{3}-2\right)^2}+\sqrt{\left(\sqrt{3}-1\right)^2}\)
3,\(\sqrt{\left(\sqrt{5}-3\right)^2}+\sqrt{\left(\sqrt{5}-2\right)^2}\)
4,\(\sqrt{\left(3+\sqrt{2}\right)^2}+\sqrt{\left(3-\sqrt{2}\right)^2}\)
5,\(\sqrt{\left(2-\sqrt{3}\right)^2}-\sqrt{\left(2+\sqrt{3}\right)^2}\)
\(1,=\left|1-\sqrt{2}\right|+\left|\sqrt{2}+3\right|\\ =1-\sqrt{2}+3+\sqrt{2}\\ =4\\ 2,=\left|\sqrt{3}-2\right|+\left|\sqrt{3}-1\right|\\ =\sqrt{3}-2+\sqrt{3}-1\\ =2\sqrt{3}-3\\ 3,=\left|\sqrt{5}-3\right|+\left|\sqrt{5}-2\right|\\ =\sqrt{5}-3+\sqrt{5}-2\\ =2\sqrt{5}-5\\ 4,=\left|3+\sqrt{2}\right|+\left|3-\sqrt{2}\right|\\ =3+\sqrt{2}+\sqrt{3}-\sqrt{2}\\ =3+\sqrt{3}\\ 5,=\left|2-\sqrt{3}\right|-\left|2+\sqrt{3}\right|\\ =2-\sqrt{3}-\left(2+\sqrt{3}\right)\\ =2-\sqrt{3}-2-\sqrt{3}\\ =-2\sqrt{3}\)
Đúng 2
Bình luận (0)
Rút gọn biểu thức A=\(\sqrt{\left(-3\right)^2}\)-\(\sqrt{\left(3-\sqrt{2}\right)^2}\)
\(A=\sqrt{\left(-3\right)^2}-\sqrt{\left(3-\sqrt{2}\right)^2}\\ =\left|-3\right|-\left|3-\sqrt{2}\right|\\ =3-3+\sqrt{2}\\=\sqrt{2}\)
Đúng 1
Bình luận (0)
Thực hiện phép tính (rút gọn biểu thức) a)sqrt{left(3+sqrt{2}right)^2}-sqrt{left(3-2sqrt{2}right)^2}b) sqrt{left(sqrt{7}-2sqrt{2}right)^2}-sqrt{left(sqrt{7}+2sqrt{2}right)^2}c)sqrt{left(3+sqrt{5}right)^2}+sqrt{left(3-sqrt{5}right)^2}d) sqrt{left(2-sqrt{3}right)^2}-sqrt{left(2+sqrt{3}right)^2}
Đọc tiếp
Thực hiện phép tính (rút gọn biểu thức)
a)\(\sqrt{\left(3+\sqrt{2}\right)^2}\)-\(\sqrt{\left(3-2\sqrt{2}\right)^2}\)
b) \(\sqrt{\left(\sqrt{7}-2\sqrt{2}\right)^2}\)-\(\sqrt{\left(\sqrt{7}+2\sqrt{2}\right)^2}\)
c)\(\sqrt{\left(3+\sqrt{5}\right)^2}\)+\(\sqrt{\left(3-\sqrt{5}\right)^2}\)
d) \(\sqrt{\left(2-\sqrt{3}\right)^2}\)-\(\sqrt{\left(2+\sqrt{3}\right)^2}\)
Lời giải:
a. $=|3+\sqrt{2}|-|3-2\sqrt{2}|=(3+\sqrt{2})-(3-2\sqrt{2})$
$=3\sqrt{2}$
b. $=|\sqrt{7}-2\sqrt{2}|-|\sqrt{7}+2\sqrt{2}|$
$=(2\sqrt{2}-\sqrt{7})-(\sqrt{7}+2\sqrt{2})$
$=-2\sqrt{7}$
c.
$=|3+\sqrt{5}|+|3-\sqrt{5}|=(3+\sqrt{5})+(3-\sqrt{5})=6$
d.
$=|2-\sqrt{3}|-|2+\sqrt{3}|=(2-\sqrt{3})-(2+\sqrt{3})=-2\sqrt{3}$
Đúng 1
Bình luận (0)
3/ rút gọn biểu thức
A=\(\left(\sqrt{a}+2\right)\left(\sqrt{a}-3\right)-\left(\sqrt{a}+1\right)^2+\sqrt{9a}\)
\(A=a+2\sqrt{a}-3\sqrt{a}-6-a-2\sqrt{a}-1+3\sqrt{a}\)
\(A=-7\)
Đúng 0
Bình luận (0)
Ta có: \(A=\left(\sqrt{a}+2\right)\left(\sqrt{a}-3\right)-\left(\sqrt{a}+1\right)^2+\sqrt{9a}\)
\(=a-3\sqrt{a}+2\sqrt{a}-6-a-2\sqrt{a}-1+3\sqrt{a}\)
\(=-7\)
Đúng 0
Bình luận (0)