Một hình vuông ABCD có diện tích là 144cm2. Gọi M là trung điểm của AB. N trên cạnh AD sao cho AN = 2.ND. Tính diện tích tam giác CMN

Những câu hỏi liên quan
Cho hình chữ nhật ABCD có diện tích bằng 2020. Gọi M là trung điểm của AB và N là điểm của cạnh AD sao cho AN = 2 ND . Hai đoạn thẳng CM và BN cắt nhau tại K. tính diện tích của tam giác KBC.?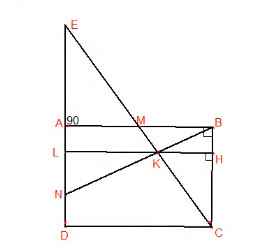
Cho hình vuông ABCD có cạnh bằng 12 cm.
a, Tính diện tích hình vuông ABCD
b,Gọi M , N là trung điểm của AB và BC . I là giao điểm của MC và ND . Tính diện tích tam giác INC
a ) Diện tích hình vuông ABCD là :
12 x 12 = 144 (cm2)
Đúng 1
Bình luận (0)
a diện tích ABCD là
12x12=144[cm2]
Đúng 0
Bình luận (0)
b ) Có : N là trung điểm của BC => NB=NC = \(\frac{1}{2}\)x BC =6 ( cm)
Diện tích hình tam giác INC là :
(6x12):2 = 36
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình chữ nhật ABCD có AD = 8cm, AB = 9cm. Các điểm M, N trên đường chéo BD sao cho BM = MN = ND. Tính diện tích tam giác CMN
A. 12cm2
B. 24 c m 2
C. 36 c m 2
D. 6 c m 2
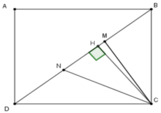
Ta có CD = AB = 9cm; BC = AD = 8cm nên SBCD = 1 2 BC.DC = 1 2 .8.9 = 36cm2
Kẻ CH ⊥ BD tại H
Ta có: SBCD = 1 2 CH.BD; SCMN = 1 2 CH.MN mà MN = 1 3 BD
=> SCMN = 1 3 SBCD = 1 3 .36 = 12cm2
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có AD=8cm, AB=9cm. Các điểm M,N trên đường chéo BD sao cho BM=MN=ND. Tính diện tích tam giác CMN.
Diện tích hình chữ nhật ABCD là:
8x9 =72 (cm^2)
S ABD= S BDC = 1/2 S ABCD
S CMN = 1/3 S BDC
Suy ra: S CMN = 1/6 S ABCD
Diện tích tam giác CMN là:
72 .1/6 =12 (cm^2)
S là kí hiệu của diện tích. Chúc bạn học tốt
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có AB = 6 cm, AD = 18 cm. Lấy điểm M trên cạnh AB và điểm N trên cạnh AD sao cho AM = 1 3 x AB và ND = 1 2 x AN. Tính diện tích tam giác MNC.
Diện tích hình chữ nhật ABCD là:
18 x 6 = 108 ( cm2)
cạnh ND dài là:
18 x ⅔ = 12 ( cm )
Diện tích tam giác NDC là:
12 x 6 : 2 = 36 ( cm2)
Cạnh AN dài là:
6 x 2 = 12 ( cm )
Cạnh AM dài là:
6 x ⅓ = 2 ( cm )
Diện tích Tam giác ANM là:
12 x 2 : 2 = 12 ( cm2)
Cạnh MB dài là:
6 x ⅔ = 4 ( cm )
Diện tích Tam giác MBC là:
18 x 4 : 2= 36 ( cm2)
Tổng diện tích tam giác ANM, NDC, MBC là:
12 + 36 + 36 = 84 ( cm2)
Diện tích tam giác MNC là:
108 - 84 = 24 ( cm2)
Đáp số : 24 cm2
Đây là bài giải của mình mn thấy đúng thì tick để mình soát bài mình nhé. Thanks ak <3
Đúng 2
Bình luận (0)
Cho ABCD là hình bình hành. M là điểm trên cạnh AD sao cho AM=2MD. N là điểm trên cạnh AB sao cho AN= 2NB. Đoạn BM cắt đoạn DN tại điểm O. Biết diện tích hình bình hành ABCD là 60cm2. Tính tổng diện tích của tam giác BON và diện tích tam giác DOM
Cho hình chữ nhật ABCD có AD=6cm
Tính diện tích hình chữ nhật ABCD?
Lấy điểm M trên cạnh AB điểm N trên cạnh CD sao cho AM =CN.Nối M với N so sánh diện tích hình AMND và MBCN
Gọi I là trung điểm của BC nối M với I,N.Tính diện tích tam giác IMN?
mình biết nội quy rồi nên đưng đăng nội quy
ai chơi bang bang 2 kết bạn với mình
mình có nick có 54k vàng đang góp mua pika
ai kết bạn mình cho
Đúng 0
Bình luận (0)
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
bài 1: Cho tam giác ABC có diện tích là 160cm2 và M là trung điểm chính giữa của cạnh AB
a) Tính diện tích tam giác ACM
b) Tìm trên cạnh AC một điểm N sao cho diện tích tam giác AMN bằng 20cm2.
bài 2: Cho tam giác ABC. trên cạnh BC lấy điểm M sao cho BM= 2MC, trên cạnh AC lấy điểm N sao cho CN=3NA. Tính diện tích tam giác CMN là 20cm2
Cho hình thang vuông ABCD , AD 6cm ; DC 12cm ; AB 2/3 DC. a) Tính diện tích hình thang ABCD. b) Kéo dài cạnh bên AD và CB, chúng gặp nhau tại M . Tính độ dài cạnh AM. Cho hình chữ nhật ABCD có diện tích 360cm2. Trên cạnh AB lấy 2 điểm M và N sao cho AM1/2AB, AN1/3AB. Gọi giao điểm của DM và CN là O. Tính diện tích tam giác MON. Cho hình chữ nhật ABCD, trên cạnh BC lấy điểm M sao cho BM MC, trên cạnh CD lấy N sao cho NC 1/3xDC. Hãy so...
Đọc tiếp
Cho hình thang vuông ABCD , AD= 6cm ; DC = 12cm ; AB = 2/3 DC.
a) Tính diện tích hình thang ABCD.
b) Kéo dài cạnh bên AD và CB, chúng gặp nhau tại M . Tính độ dài cạnh AM.
Cho hình chữ nhật ABCD có diện tích 360cm2. Trên cạnh AB lấy 2 điểm M và N sao cho AM=1/2AB, AN=1/3AB. Gọi giao điểm của DM và CN là O. Tính diện tích tam giác MON.
Cho hình chữ nhật ABCD, trên cạnh BC lấy điểm M sao cho BM = MC, trên cạnh CD lấy N sao cho NC = 1/3xDC. Hãy so sánh diện tích hình tam giác AMN với diện tích hình tam giác ADN
HCN có diện tích 360 cm2.Tính diện tích HCN với số đo chiều dài và chiều rộng tương ứng là 3/2số đo HCN đã cho
Cho hình tam giác ABC. Trên AB lấy điểm M sao cho AM = 1/3 AB. Trên AC lấy điểm N sao cho AN = 1/4 AC. Nối M với C, nối N với B cắt nhau tại O. Hãy so sánh diện tích tam giác BOC và diện tich tam giác ABC.
1)
a) Cạnh AB là : 12 x 2/3 = 8 (cm)
Diện tích ABCD là : (8 + 12) : 2 x 6 = 60 (cm2)
b) -Xét tam giác ABC đáy AB và DBC đáy CD có chiều cao bằng nhau = 6cm mà đáy AB = 2/3 CD => S_ABC = 2/3 S_DBC.
Vẫn xét 2 tam giác ABC và DBC chung đáy BC vì S_ABC = 2/3 S_DBC => chiều cao AK = 2/3 DH.
-Xét tam giác AMC và DMC chung đáy MC mà chiều cao AK = 2/3 DH => S_AMC = 2/3 S_DMC. Mà S_DMC lớn hơn S_AMC là : 12 x 6 : 2 = 36 (cm2)
S_AMC là : 36 : (3-2) x 2 = 72 (cm2) (Toán Hiệu - Tỉ)
Xét tam giác AMC đáy AM, chiều cao CD => AM = 72 x 2 : 12 = 12 (cm)
2)
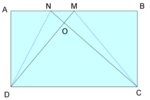
Ta có:
MN = 1/2 AB - 1/3 AB = 1/6 AB
Xét tam giác NMD và MCD có chiều cao = chiều rộng hình chữ nhật mà đáy NM = 1/6 CD => S_NMD = 1/6 S_MCD. Mà S_MCD = 360 : 2 = 180 (cm2) => S_NMD = 180 : 6 = 30 (cm2)
Mặt khác 2 tam giác này chugn đáy MD => Chiều cao tam giác NMD đỉnh N = 1/6 chiều cao tam giác MCD đỉnh C
Xét tam giác NMD và NMC chung đáy NM chiều cao bằng nhau => S_NMD = S_NMC = 30 (cm2)
Xét tam giác NMO và MCO có chung đáy MO chiều cao tam giác NMO = 1/6 chiều cao MCO => S_NMO = 1/6 S_MCO
Vậy diện tích NMO là : 30 : (1 + 6) = 30/7 (cm2
3)
Diện tích hình chữ nhật: S=a.b
S_ADN= 2/3a x b : 2 = 1/3 ab = 1/3S
Ta có:
S_AMN = (S_AMC + S_ANC) – S_MCN= (MC x AB :2 + NC x AD : 2) – (NC x MC : 2)
= (1/2b x a : 2 + 1/3a x b : 2) – (1/3a x 1/2b : 2)
= ¼ S + 1/6S - 1/12S
= 5/12 S – 1/12 S = 4/12 S = 1/3 S
Gọi S=a x b
S_tăng = 3/2a x 3/2b = 9/4 S
Diện tích mới: 360 x 9/4 = 810 (cm2)
Nối A với O.
Ta có: SABN = 1/3 SBNC nên đường cao kẻ từ A và C xuống NB có tỉ lệ 1/3
Suy ra SABO = 1/3 SBOC (chung đáy OB)
Tương tự:
SAMC = 1/2SBMC nên dường cao kẻ từ A và B xuống MC có tỉ lệ 1/2
Suy ra SAOC = 1/2 SBOC (chung đáy OC)
Từ đó ta có: SAOC + SAOB = (1/3+1/2)SBOC = 5/6 SBOC
SAOC + SAOB có 5 phần thì SBOC có 6 phần và SABC có (5+6) 11 phần
Vậy: AOCB = 6/11 SABC
Đúng 0
Bình luận (0)
a) Cạnh AB là : 12 x 2/3 = 8 (cm)
Diện tích ABCD là : (8 + 12) : 2 x 6 = 60 (cm2)
b) -Xét tam giác ABC đáy AB và DBC đáy CD có chiều cao bằng nhau = 6cm mà đáy AB = 2/3 CD => S_ABC = 2/3 S_DBC.
Vẫn xét 2 tam giác ABC và DBC chung đáy BC vì S_ABC = 2/3 S_DBC => chiều cao AK = 2/3 DH.
-Xét tam giác AMC và DMC chung đáy MC mà chiều cao AK = 2/3 DH => S_AMC = 2/3 S_DMC. Mà S_DMC lớn hơn S_AMC là : 12 x 6 : 2 = 36 (cm2)
S_AMC là : 36 : (3-2) x 2 = 72 (cm2) (Toán Hiệu - Tỉ)
Xét tam giác AMC đáy AM, chiều cao CD => AM = 72 x 2 : 12 = 12 (cm)
2)

Ta có:
MN = 1/2 AB - 1/3 AB = 1/6 AB
Xét tam giác NMD và MCD có chiều cao = chiều rộng hình chữ nhật mà đáy NM = 1/6 CD => S_NMD = 1/6 S_MCD. Mà S_MCD = 360 : 2 = 180 (cm2) => S_NMD = 180 : 6 = 30 (cm2)
Mặt khác 2 tam giác này chugn đáy MD => Chiều cao tam giác NMD đỉnh N = 1/6 chiều cao tam giác MCD đỉnh C
Xét tam giác NMD và NMC chung đáy NM chiều cao bằng nhau => S_NMD = S_NMC = 30 (cm2)
Xét tam giác NMO và MCO có chung đáy MO chiều cao tam giác NMO = 1/6 chiều cao MCO => S_NMO = 1/6 S_MCO
Vậy diện tích NMO là : 30 : (1 + 6) = 30/7 (cm2
3)
AB=a ; BC=b
Diện tích hình chữ nhật: S=a.b
S_ADN= 2/3a x b : 2 = 1/3 ab = 1/3S
Ta có:
S_AMN = (S_AMC + S_ANC) – S_MCN= (MC x AB :2 + NC x AD : 2) – (NC x MC : 2)
= (1/2b x a : 2 + 1/3a x b : 2) – (1/3a x 1/2b : 2)
= ¼ S + 1/6S - 1/12S
= 5/12 S – 1/12 S = 4/12 S = 1/3 S
Gọi S=a x b
S_tăng = 3/2a x 3/2b = 9/4 S
Diện tích mới: 360 x 9/4 = 810 (cm2)
Nối A với O.
Ta có: SABN = 1/3 SBNC nên đường cao kẻ từ A và C xuống NB có tỉ lệ 1/3
Suy ra SABO = 1/3 SBOC (chung đáy OB)
Tương tự:
SAMC = 1/2SBMC nên dường cao kẻ từ A và B xuống MC có tỉ lệ 1/2
Suy ra SAOC = 1/2 SBOC (chung đáy OC)
Từ đó ta có: SAOC + SAOB = (1/3+1/2)SBOC = 5/6 SBOC
SAOC + SAOB có 5 phần thì SBOC có 6 phần và SABC có (5+6) 11 phần
Vậy: AOCB = 6/11 SABC
Đúng 0
Bình luận (0)
a) Cạnh AB là : 12 x 2/3 = 8 (cm)
Diện tích ABCD là : (8 + 12) : 2 x 6 = 60 (cm2)
b) -Xét tam giác ABC đáy AB và DBC đáy CD có chiều cao bằng nhau = 6cm mà đáy AB = 2/3 CD => S_ABC = 2/3 S_DBC.
Vẫn xét 2 tam giác ABC và DBC chung đáy BC vì S_ABC = 2/3 S_DBC => chiều cao AK = 2/3 DH.
-Xét tam giác AMC và DMC chung đáy MC mà chiều cao AK = 2/3 DH => S_AMC = 2/3 S_DMC. Mà S_DMC lớn hơn S_AMC là : 12 x 6 : 2 = 36 (cm2)
S_AMC là : 36 : (3-2) x 2 = 72 (cm2) (Toán Hiệu - Tỉ)
Xét tam giác AMC đáy AM, chiều cao CD => AM = 72 x 2 : 12 = 12 (cm)
2.
Ta có:
MN = 1/2 AB - 1/3 AB = 1/6 AB
Xét tam giác NMD và MCD có chiều cao = chiều rộng hình chữ nhật mà đáy NM = 1/6 CD => S_NMD = 1/6 S_MCD. Mà S_MCD = 360 : 2 = 180 (cm2) => S_NMD = 180 : 6 = 30 (cm2)
Mặt khác 2 tam giác này chugn đáy MD => Chiều cao tam giác NMD đỉnh N = 1/6 chiều cao tam giác MCD đỉnh C
Xét tam giác NMD và NMC chung đáy NM chiều cao bằng nhau => S_NMD = S_NMC = 30 (cm2)
Xét tam giác NMO và MCO có chung đáy MO chiều cao tam giác NMO = 1/6 chiều cao MCO => S_NMO = 1/6 S_MCO
Vậy diện tích NMO là : 30 : (1 + 6) = 30/7 (cm2)
3.
AB=a ; BC=b
Diện tích hình chữ nhật: S=a.b
S_ADN= 2/3a x b : 2 = 1/3 ab = 1/3S
Ta có:
S_AMN = (S_AMC + S_ANC) – S_MCN= (MC x AB :2 + NC x AD : 2) – (NC x MC : 2)
= (1/2b x a : 2 + 1/3a x b : 2) – (1/3a x 1/2b : 2)
= ¼ S + 1/6S - 1/12S
= 5/12 S – 1/12 S = 4/12 S = 1/3 S
Gọi S=a x b
S_tăng = 3/2a x 3/2b = 9/4 S
Diện tích mới: 360 x 9/4 = 810 (cm2)
Nối A với O.
Ta có: SABN = 1/3 SBNC nên đường cao kẻ từ A và C xuống NB có tỉ lệ 1/3
Suy ra SABO = 1/3 SBOC (chung đáy OB)
Tương tự:
SAMC = 1/2SBMC nên dường cao kẻ từ A và B xuống MC có tỉ lệ 1/2
Suy ra SAOC = 1/2 SBOC (chung đáy OC)
Từ đó ta có: SAOC + SAOB = (1/3+1/2)SBOC = 5/6 SBOC
SAOC + SAOB có 5 phần thì SBOC có 6 phần và SABC có (5+6) 11 phần
Vậy: AOCB = 6/11 SABC
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình vuông ABCD có cạnh bằng a, trên các cạnh AB, AD lần lượt lấy hai điểm M,N sao cho tam giác AMN có chu vi bằng 2a. Tìm vị trí của M, N để diện tích tam giác CMN lớn nhất.
Đặt AM=x; AN=y
MN^2=AM^2+AN^2
=>\(MN=\sqrt{x^2+y^2}\)
\(P_{AMN}=AM+AN+MN=x+y+\sqrt{x^2+y^2}=2a\)
và x+y>=2*căn xy; \(\sqrt{x^2+y^2}>=\sqrt{2xy}\)
=>\(2a=x+y+\sqrt{x^2+y^2}>=2\sqrt{xy}+\sqrt{2xy}\)
=>\(2a>=\sqrt{xy}\left(2+\sqrt{2}\right)\)
=>\(\sqrt{xy}< =\dfrac{2a}{2+\sqrt{2}}\)
=>\(S_{AMN}=\dfrac{1}{2}xy< =\dfrac{1}{2}\cdot\left(\dfrac{2a}{2+\sqrt{2}}\right)^2=\left(3-2\sqrt{2}\right)a^2\)
Dấu = xảy ra khi \(x=y=\left(2-\sqrt{2}\right)a\)
Đúng 1
Bình luận (0)





















