Ta có CD = AB = 9cm; BC = AD = 8cm nên SBCD = 1 2 BC.DC = 1 2 .8.9 = 36cm2
Kẻ CH ⊥ BD tại H
Ta có: SBCD = 1 2 CH.BD; SCMN = 1 2 CH.MN mà MN = 1 3 BD
=> SCMN = 1 3 SBCD = 1 3 .36 = 12cm2
Đáp án cần chọn là: A
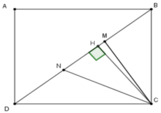
Cho hình chữ nhật ABCD có AD=8cm, AB=9cm. Các điểm M,N trên đường chéo BD sao cho BM=MN=ND. Tính diện tích tam giác CMN.
Cho hình chữ nhật ABCD có AB = 20cm, AD = 15cm a) Tính độ dài đường chéo BD b) Trên cạnh AD lấy điểm M sao cho AM = 5cm. CM cắt BD tại P và đường thẳng AB tại Q. Tính tỉ số diện tích 2 tam giác PDM và PBC c) Gọi N là trung điểm của cạnh AB. C/m: 2 tam giác AMN và DMC đồng dạng d) C/m: MA là tia phân giác của góc QMN
Cho hình chữ nhật ABCD có cạnh AB=5cm và diện tích bằng 30cm2 .Lấy M,N lần lượt trên BC và AD sao cho BM=DN =2cm
a) Tính diện tích hình thang ABMN và diện tích tam giác CMN
b) Tinh đường cao hạ từ D của tam giác CDN
1. Cho hình thoi ABCD có số đo góc A bằng 1200. Gọi O là giao điểm của hai đường chéo AC và BD. Trên tia BC lấy điểm M sao cho BM=4/3BC. Đường thẳng AM cắt CD tại N. Trên các đoạn thẳng AB, AD lần lượt lấy các điểm E, F sao cho CE//NF. Tính số đo góc EOF
2. Cho điểm D thay đổi trên cạnh BC của tam giác nhọn ABC (D khác B và C). Từ D kẻ đường thẳng song song với AB cắt cạnh AC tại điểm N. Cũng từ D kẻ đường thẳng song song với AC cắt cạnh AB tại điểm M. Tìm vị trí của D để đoạn thẳng MN có độ dài nhỏ nhất.
3.. ABCD là hình chữ nhật có AB //CD, AB = 2CB. Từ A kẻ đường thẳng vuông góc với đường chéo BD tại H. Trên HB lấy điểm K sao cho HK = HA. Từ K kẻ đường thẳng song song với AH cắt AB tại E. Lấy M trung điểm DE, tia AM cắt DB tại N, cắt DC tại P.
Tính tỷ số diện tích tam giác AND với diện tam giác PMD?
Cho hình bình hành ABCD có AB= 8cm ,AD=6cm. Trên cạnh BC lấy điểm M sao cho BM=4cm. Đường thẳng AM cắt đường chéo BD tại I, cắt đường thẳng BC tại N.
a. tính tỉ số IB = ID
b. CM: Tam giác AMB đồng dạng tam giác AND. Tính độ dài DN và CN
c. CM . IA^2 = IM.IN
Cho hình chữ nhật ABCD có cạnh AB =5cm và diện tích bằng 30 cm2 . Lấy M,N lần lượt trên cạnh BC và AD sao cho BM=DN=2cm.
a) Tính diện tích hình thang ABMN và diện tích tam giác CMN
b) Tính đường cao hạ từ D của tam giác CDN
1.Cho tam giác ABCcân tại A có AB = AC = 100cm, BC = 120cm. Hai đường cao AD, BE cắt nhau tại H.a)Tìm các tam giác đồng dạng với tam giác BDHb)Tình độ dài các đoạn: HD, AH, BH, EH
2.Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Đường cao AH, đường phân giác BDa)Tình độ dài AD, DCb)Gọi I là giao điểm của AH và BD. C/m: AB.BI = BD.HBc)C/m: Tam giác AID cân
3.Cho hình thang cân ABCD (AB//CD), AB < CD. Đường cao BH chia cạnh CD thành 2 đoạn DH = 16cm, HC = 9cm. Biết BD vuông góc BC.a)Tính đường chéo AC và BD của hình thangb)Tính diện tích hình thangc)Tính chu vi hình thang
Cho HCN ABCD có AB=5cm và diện tích =30cm2 .Lấy M,N trên BC và AD sao cho BM=DN=2cm
a)Tính diện tích hình thang ABMN và diện tích tem giác CMN
b)Tính đường cao hạ từ D của tam giác CDN
Cho hình chữ nhật ABCD, có AB = m , BC = n , m<n. Trên cạnh AD lấy 1 điểm M sao cho BM =n ; tia phân giác góc MBC cắt cạnh CD tại N. Gọi I là giao điểm của MN và AB.
a. TÍnh các đoạn thẳng IA,IB, IN theo m và n.
b, từ C hạ đường vuông góc với BD tại K. Chứng minh rằng C,K,I thẳng hàng.
