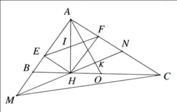
Cho tam giác ABC vuông tại A. Kẻ AH ⊥ BC ( H thuộc BC ), gọi M và N lần lượt là hình chiếu vuông góc của H trên AB, AC. Đường thẳng đi qu A cắt HM tại E và cắt tia đối của HN tại F. Chứng minh BE song song CF
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường cao AH. Trên tia đối của tia AB lấy điểm K sao cho góc AKC = 600. D và E lần lượt là hình chiếu của H trên AB, AC. Qua A kẻ đường thẳng vuông góc với DE cắt BC tại M (M thuộc BC). Kẻ tia Cx là tia phân giác của góc ACB, qua M kẻ đường thẳng song song với AC cắt Cx tại F. Chứng minh BF vuông góc CF.
Gọi AM cắt DE tại I
Theo tính chất hình chữ nhật ADHE : \(\widehat{E_1}=\widehat{HAC}=\widehat{MBA};\widehat{A_1}=\widehat{D_1}=\widehat{AHE}=\widehat{MCA}\)
\(\Rightarrow\widehat{A_1}=\widehat{ACM}\Rightarrow\Delta ACM\)cân tại M \(\Rightarrow MA=MC\)(*)
Do \(\Delta AID\)vuông tại I suy ra
\(\widehat{DAM}+\widehat{D_1}=90^0\Leftrightarrow\widehat{DAM}+\widehat{DAH}=90^0\left(1\right)\)
\(\widehat{ABM}+\widehat{DAH}=90^0\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{DAM}=\widehat{ABM}\)
\(\Rightarrow\Delta ABM\)cân tại M \(\Rightarrow MA=MB\)(**)
Từ (*);(**) suy ra MB=MC hay M là trung điểm BC . Do MF//AC suy ra
\(\widehat{MFC}=\widehat{ACF}\)
Mà
\(\widehat{ACF}=\widehat{MCF}\Rightarrow\widehat{MFC}=\widehat{MCF}\Rightarrow\Delta MFC\)cân tại M suy ra MC=MF
Mà MB=MC suy ra 
\(\Delta BFC\) có FM là trung tuyến 
\(FM=\frac{1}{2}BC\Rightarrow\) \(\Delta BFC\)vuông tại F hay 
\(BF\perp CF\left(đpcm\right)\)
bấm nhầm gửi câu hỏi nha
cho tam giác ABC cân tại A .Qua A kẻ đường thẳng vuông góc với BC gọi là AH. Kẻ HM vuông góc AB ,HN vuông góc AC .
a, Chứng minh : HM = HN
b, Trên tia đối của NH lấy F sao cho NF = NH. Chứng minh: FC vuông góc AF
c , Qua H kẻ đường thẳng song song FC cắt AC tại I. Chứng minh : IF song song BC .
d, Trên tia đối của MH lấy E sao cho ME = MH. Chứng minh : E , I , F thẳng hàng
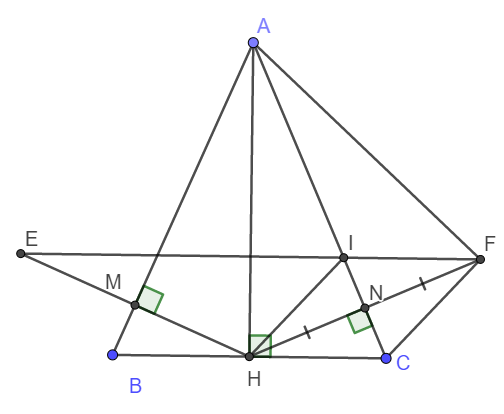
a) Do ABC là tam giác cân tại A nên AH là đường cao hay đồng thời là đường phân giác.
Xét tam giác vuông AMH và tam giác vuông ANH có:
Cạnh AH chung
\(\widehat{MAH}=\widehat{NAH}\)
\(\Rightarrow\Delta AMH=\Delta ANH\) (Cạnh huyền - góc nhọn)
\(\Rightarrow HM=HN.\)
b) Dễ dàng thấy ngay AC là đường trung trực của HF.
Khi đó thì AH = AF; CH = CF
Xét tam giác AHC và tam giác AFC có:
Cạnh AC chung
AH - AF
CH = CF
\(\Rightarrow\Delta AHC=\Delta AFC\left(c-c-c\right)\)
\(\Rightarrow\widehat{AFC}=\widehat{AHC}=90^o\Rightarrow AF\perp CF.\)
c) Ta thấy ngay \(\Delta HIN=\Delta FCN\left(g-c-g\right)\)
\(\Rightarrow IN=CN\)
Xét tam giác vuông INF và tam giác vuông CNH có:
HN = FN
IN = CN
\(\Rightarrow\Delta INF=\Delta CNH\) (Hai cạnh góc vuông)
\(\Rightarrow\widehat{IFN}=\widehat{CHN}\)
Mà chúng lại ở vị trí so le trong nên IF // BC.
d) Chứng minh tương tự câu c, ta có IE // BC
Vậy thì qua I có hai tia IE và IF cùng song song với BC nên chúng trùng nhau.
Vậy I, E, F thẳng hàng.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB>AC). Kẻ đường cao AH (H thuộc BC). Gọi D là trung điểm của AB. Qua A kẻ đường thẳng vuông góc với CD cắt CD và CB lần lượt tại E và F. Gọi K là hình chiếu vuông góc của D trên BC.
1) Chứng minh rằng các tam giác ADE và CDA đồng dạng với nhau.
2) Chứng minh rằng BD.BC = BE.CD.
Cho tam giacs ABC nội tiếp đường tròn tâm O đường kính BC.Kẻ AH vuông góc BC tại H.Gọi M,N lần lượt là hình chiếu của H trên AB,AC
a,CM AMHN là hình chữ nhật và AM.AB=AN.AC
b,CM tứ giác BMNC là tứ giác nội tiếp và AC.BM+AB.CN=AH.BC
c,Chứng minh đường thẳng đi qua A cắt HM tại E cắt tia đối NH tại F>Chứng minh BE song song CF
Cho tam giác ABC vuông tại A (AB AC). Kẻ AH vuông góc vói BC tại H. Gọi E và F lần lượt là hình chiếu của H trên AB và AC.a) Chứng minh AH2 - AE.AB.b) Chứng minh
Δ
A
F
E
~
Δ
A
B
C
;
c) Lấy M đối xứng với A qua E, tia MH cắt cạnh AC tại N. Chứng minh
A
B
H
^
A...
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC). Kẻ AH vuông góc vói BC tại H. Gọi E và F lần lượt là hình chiếu của H trên AB và AC.
a) Chứng minh AH2 - AE.AB.
b) Chứng minh Δ A F E ~ Δ A B C ;
c) Lấy M đối xứng với A qua E, tia MH cắt cạnh AC tại N. Chứng minh A B H ^ = A N H ^ và EF//HN.
d) Gọi O là trung điểm của BC; AO giao với HN tại K. Cho biết A C B ^ = 30 ° , hãy tính tỉ số A K A N S H C A
Giúp tui câu 3
cho tam giác ABC nội tiếp đường tròn tâm O đường kính BC , kẻ AH vuông góc với BC ( H thuộc BC ) .Gọi M,N lần lượt là hình chiếu của H trên AB ,AC
1) CM : AC2=CH*CB
2 ) CM BCNM nội tiếp : AC*BM+AB*CM=AH*BC
3) đường thẳng qua A cắt HM tại E cắt tia đối NH tại F chứng minh BE//CF
Cho tam giác ABC vuông tại A (AB AC). Kẻ AH vuông góc vói BC tại H. Gọi E và F lần lượt là hình chiếu của H trên AB và AC.a) Chứng minh AH2 - AE.AB.b) Chứng minh Δ A F E ~ Δ A B C ;c) Lấy M đối xứng với A qua E, tia MH cắt cạnh AC tại N. Chứng minh A B H ^ A N H ^ và EF//HN.d) Gọi O là trung điểm của BC; AO giao với HN tại K. Cho biết A C B ^ 30 ° , hãy tính tỉ số A K A N S H C A
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC). Kẻ AH vuông góc vói BC tại H. Gọi E và F lần lượt là hình chiếu của H trên AB và AC.
a) Chứng minh AH2 - AE.AB.
b) Chứng minh Δ A F E ~ Δ A B C ;
c) Lấy M đối xứng với A qua E, tia MH cắt cạnh AC tại N. Chứng minh A B H ^ = A N H ^ và EF//HN.
d) Gọi O là trung điểm của BC; AO giao với HN tại K. Cho biết A C B ^ = 30 ° , hãy tính tỉ số A K A N S H C A
a: ΔAHB vuông tại H có HE là đường cao
nên AH^2=AE*AB
b: ΔAHC vuông tại H có HF là đường cao
nên AH^2=AF*AC
=>AE*AB=AF*AC
=>AE/AC=AF/AB
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
AE/AC=AF/AB
=>ΔAEF đồng dạng với ΔACB
Đúng 0
Bình luận (0)
Cho tam giacs ABC nội tiếp đường tròn tâm O đường kính BC.Kẻ AH vuông góc BC tại H.Gọi M,N lần lượt là hình chiếu của H trên AB,AC
a,CM AMHN là hình chữ nhật và AM.AB=AN.AC
b,CM tứ giác BMNC là tứ giác nội tiếp và AC.BM+AB.CN=AH.BC
c,Chứng minh đường thẳng đi qua A cắt HM tại E cắt tia đối NH tại F>Chứng minh BE song song CF
AI GIÚP CÂU CÚI VỚI KHÓ QUÁ
Cho tam giác ABC vuông tại A có góc B = 2 góc C và BC = a (a > 0)
a/ Tính AB theo a
b/ Kẻ đường cao AH. Gọi E,F lần lượt là hình chiếu của H trên AB,AC. Chứng minh AE.AB=À=AC
c/ Qua A kẻ đường thẳng BC, cắt tia phân giác của góc ABC tại D. Gọi I,K là trung điểm của AC,BD. Tính IK theo a.
Help me I need right now PLEASE!!!
b: Xét ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
Đúng 1
Bình luận (0)
1) Cho tam giác cân ABC (ABAC). Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BDCE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB, AC lần lượt ở M,N. DMEN, đường thẳng BC cắt MN tại trung điểm I của MN. Chứng minh rằng: đường thẳng vuông góc vs MN tại I luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC.2)Cho tam giác ABC vuông tại A, K là trung điểm của cạnh BC. Qua K kẻ đường thẳng vuông góc vs AK, đường này cắt các đường thẳng AB và AC lần lượt ở D và E. Gọi...
Đọc tiếp
1) Cho tam giác cân ABC (AB=AC). Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB, AC lần lượt ở M,N. DM=EN, đường thẳng BC cắt MN tại trung điểm I của MN. Chứng minh rằng: đường thẳng vuông góc vs MN tại I luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC.
2)Cho tam giác ABC vuông tại A, K là trung điểm của cạnh BC. Qua K kẻ đường thẳng vuông góc vs AK, đường này cắt các đường thẳng AB và AC lần lượt ở D và E. Gọi I là trung điểm của DE.
a)Chứng minh rằng: AI vuông góc vs BC
b) Có thể nói DE nhỏ hơn BC được không? Vì sao?
3) Cho tam giác ABC (AB>AC), M là trung điểm của BC. Đường thẳng đi qua M và vuông góc vs tia phân giác của góc A tại H cắt hai tia AB, AC lần lượt tại E và F. CMR:
a) EF^2/4 +AH^2=AE^2
b) 2BME=ACB-B
c) BE=CF
4)Cho tam giác ABC có góc B và C là 2 góc nhọn. Trên tia đối của tia AB lấy điểm D sao cho AD=AB, trên tia đối của tia AC lấy điểm E sao cho AE=AC. M là trung điểm của BE, N là trung điểm CB. Ax là tia bất kỳ nằm gưac 2 tia AB và AC. Gọi H, K lần lượt là hình chiếu của B và C trên tia Ax. Xác định vị trí của tia Ax để tổng BH+CK có giá trị lớn nhất.
5)Cho tam giác ABC có 3 góc nhọn, đường cao AH, ở miền ngoài của tam giác ABC ta vẽ các tam giác vuông cân ABE và ACF đều nhận A làm đỉnh góc vuông. Kẻ EM, FN cùng vuông
góc vs AH (M,N thuộc AH)
a) CM: EM+HC=NH
b) CM: EN // FM
bạn đăng từng bài lên 1 đi
mik giải dần cho
Đúng 0
Bình luận (0)
Cho DABC vuông tại C . Trên cạnh AB lấy điểm D sao cho AD = AB. Kẻ qua D đường thẳng vuông góc với AB cắt BC tại E. AE cắt CD tại I.
a) Chứng minh AE là phân giác góc CAB
b) Chứng minh AD là trung trực của CD
c) So sánh CD và BC
d) M là trung điểm của BC, DM cắt BI tại G, CG cắt DB tại K. Chứng minh K là trung điểm của DB.
Đúng 0
Bình luận (0)