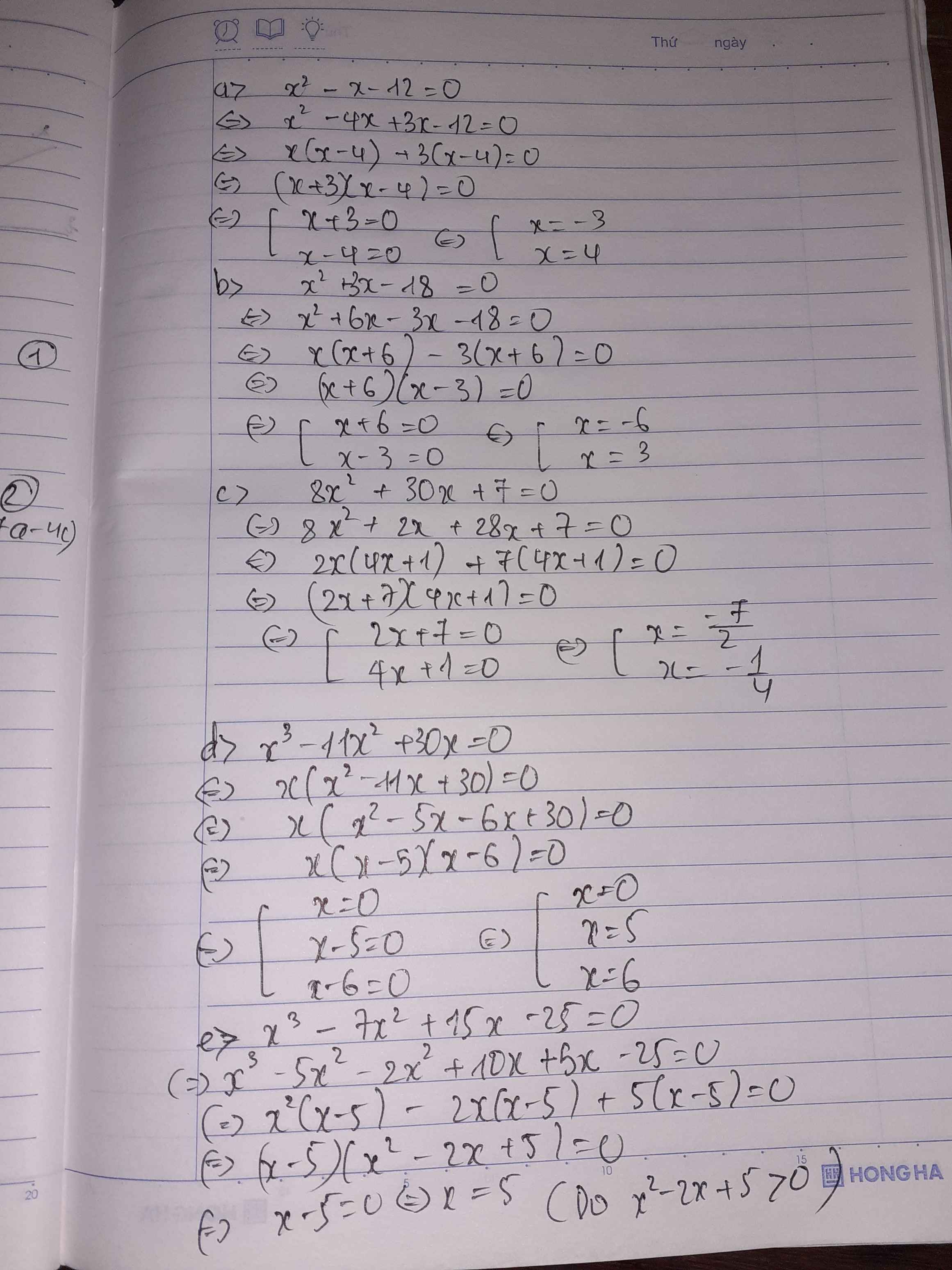3x^4+15x^3-30x-10/x-5

Những câu hỏi liên quan
tìm x
a)x^2-x-12=0
b)x^2+3x-18=0
c)8x^2+30x+7=0
d)x^3-11x^2+30x=0
e)x^3-7x^2+15x-25=0
giúp mk vs ah!!!!!
a) Ta có: \(x^2-x-12=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
Đúng 0
Bình luận (0)
b) Ta có: \(x^2+3x-18=0\)
\(\Leftrightarrow\left(x+6\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-6\\x=3\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giari phương trình
30x^4+19x^3-15x^2-3x+1
Phương trình phải có vế phải bạn nhé!
Đúng 0
Bình luận (0)
bài 1 : thực hiện phép tính
a) (4x - 1)(2 - x)-(2x-1)^2
b) (15x^4y^5-30x^3y^4+35x^3y^4): (5x^3y^3)
a) (4x-1)(2-x)-(2x-1)2
= 8x-4x2-2+x-(4x2-4x+1) = -8x2+13x-3
b) (15x4y5-30x3y4+35x3y4):(5x3y3)
= 3xy2-6y+7y = 3xy2+y
Đúng 0
Bình luận (0)
a: \(=8x-4x^2-2+2x-4x^2+4x-1\)
\(=-8x^2+14x-3\)
Đúng 0
Bình luận (0)
Cho \(x=\dfrac{3+\sqrt{5}}{2}\). Tình \(P=\left(10x^2-30x+11\right)^2+\dfrac{\left(2x^2-6x+3\right)^{10}}{x^5-3x^4+x^3-1}\)
\(x=\dfrac{3+\sqrt{5}}{2}\Rightarrow2x-3=\sqrt{5}\Rightarrow4x^2-12x+9=5\)
\(\Rightarrow4x^2-12x+4=0\Rightarrow x^2-3x+1=0\)
\(\Rightarrow P=\left[10\left(x^2-3x+1\right)+1\right]^2+\dfrac{\left[2\left(x^2-3x+1\right)+1\right]^{10}}{x^3\left(x^2-3x+1\right)-1}=1^2+\dfrac{1^2}{0-1}=...\)
Đúng 4
Bình luận (0)
Tính giá trị biểu thức
A=x^3-30x^2-31x+1 tại x=30
B=x^5-15x^4+16x^3-29x^2+13x tại x=14
x^2*(x-30)-31x+1
thay x=31 vao bieu thuc
(31)^2*(31-30)-31*31+1=1
Đúng 0
Bình luận (0)
a)\(\dfrac{3x}{2}+\dfrac{4x-3}{10}-\dfrac{15x-1}{5}\)
b)\(\dfrac{x-4}{x+1}+\dfrac{x+1}{x}=2\)
a: \(=\dfrac{5\cdot3x+4x-3-2\left(15x-1\right)}{10}=\dfrac{19x-3-30x+2}{10}=\dfrac{-11x-1}{10}\)
b: \(\Leftrightarrow x\left(x-4\right)+\left(x+1\right)^2=2x\left(x+1\right)\)
\(\Leftrightarrow x^2-4x+x^2+2x+1=2x^2+2x\)
=>-2x+1=2x
=>-4x=-1
hay x=1/4(nhận)
Đúng 0
Bình luận (0)
\(a,\dfrac{3x}{2}+\dfrac{4x-3}{10}-\dfrac{15x-1}{5}\)
\(=\dfrac{3x.5+4x-3-2\left(15x-1\right)}{10}\)
\(=\dfrac{15x+4x-3-30x+3}{10}\)
\(=\dfrac{-11x}{10}\)
Đúng 0
Bình luận (0)
Cho �3�163x16y. Tìm �x; �y biết �+�190x+y190.
�30x30; �160y160.
�15x15; �175y175.
�20x20; �170y170.
�10x10; �180y180.
Đọc tiếp
Cho . Tìm ; biết .
; . ; . ; . ; .Lời giải:
$3x=16y\Rightarrow \frac{x}{16}=\frac{y}{3}$
Áp dụng TCDTSBN:
$\frac{x}{16}=\frac{y}{3}=\frac{x+y}{16+3}=\frac{190}{19}=10$
$\Rightarrow x=10.16=160; y=3.10=30$
Đáp án A.
Đúng 4
Bình luận (0)
Bài 5: Giải các phương trình sau:a. (3x - 1)2 - (x + 3)2 0b. x3 dfrac{x}{49}c. x2 - 7x + 12 0d. 4x2 - 3x -1 0e. x3 - 2x - 4 0f. x3 + 8x2 + 17x +10 0g. x3 + 3x2 + 6x + 4 0h. x3 - 11x2 + 30x 0
Đọc tiếp
Bài 5: Giải các phương trình sau:
a. (3x - 1)2 - (x + 3)2 = 0
b. x3 = \(\dfrac{x}{49}\)
c. x2 - 7x + 12 = 0
d. 4x2 - 3x -1 = 0
e. x3 - 2x - 4 = 0
f. x3 + 8x2 + 17x +10 = 0
g. x3 + 3x2 + 6x + 4 = 0
h. x3 - 11x2 + 30x = 0
a. (3x - 1)2 - (x + 3)2 = 0
\(\Leftrightarrow\left(3x-1+x+3\right)\left(3x-1-x-3\right)=0\)
\(\Leftrightarrow\left(4x+2\right)\left(2x-4\right)=0\)
\(\Leftrightarrow4x+2=0\) hoặc \(2x-4=0\)
1. \(4x+2=0\Leftrightarrow4x=-2\Leftrightarrow x=-\dfrac{1}{2}\)
2. \(2x-4=0\Leftrightarrow2x=4\Leftrightarrow x=2\)
S=\(\left\{-\dfrac{1}{2};2\right\}\)
Đúng 3
Bình luận (0)
b. \(x^3=\dfrac{x}{49}\)
\(\Leftrightarrow49x^3=x\)
\(\Leftrightarrow49x^3-x=0\)
\(\Leftrightarrow x\left(49x^2-1\right)=0\)
\(\Leftrightarrow x\left(7x+1\right)\left(7x-1\right)=0\)
\(\Leftrightarrow x=0\) hoặc \(7x+1=0\) hoặc \(7x-1=0\)
1. x=0
2. \(7x+1=0\Leftrightarrow7x=-1\Leftrightarrow x=-\dfrac{1}{7}\)
3. \(7x-1=0\Leftrightarrow7x=1\Leftrightarrow x=\dfrac{1}{7}\)
Đúng 2
Bình luận (0)
*Cách khác:
a) Ta có: \(\left(3x-1\right)^2-\left(x+3\right)^2=0\)
\(\Leftrightarrow\left(3x-1\right)^2=\left(x+3\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=-x-3\\3x-1=x+3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x=-2\\2x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=2\end{matrix}\right.\)
Vậy: \(S=\left\{-\dfrac{1}{2};2\right\}\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
C/m đẳng thức:
a) \(\frac{3y}{4}\) = \(\frac{6xy}{8x}\)
b) \(\frac{10}{15x}\) = \(\frac{20xy}{30x^2y}\)
c) \(\frac{3x^3y^5}{2xy^6}\) = \(\frac{3x^2}{2y}\)
\(a,\frac{3y}{4}=\frac{6xy}{8x}\\\frac{3y}{4}=\frac{3y.2x}{4.2x}=\frac{6xy}{8x}\)
\(b,\frac{10}{15x}=\frac{20xy}{30x^2y}\\ \frac{10}{15x}=\frac{10.2xy}{15x.2xy}=\frac{20xy}{30x^2y}\)
\(c,\frac{3x^3y^5}{2xy^6}=\frac{3x^2}{2y}\\ \frac{3x^2}{2y}=\frac{3x^2.x.y^5}{2y.x.y^5}=\frac{3x^3y^5}{2xy^6}\)
Đúng 0
Bình luận (0)