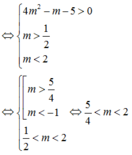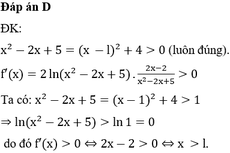Cho hàm số f(x) = x2 -1 . Tìm các giá trị của x sao cho f(1-x) nhận giá trị âm
Những câu hỏi liên quan
Cho hàm số yf(x) có đạo hàm
f
(
x
)
x
2
(
x
+
1
)
(
x
2
+
2
m
x
+
4
)
. Có bao nhiêu giá trị nguyên âm của tham số m để hàm số
y
f
(
x
)
2
có đúng một điể...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x 2 ( x + 1 ) ( x 2 + 2 m x + 4 ) . Có bao nhiêu giá trị nguyên âm của tham số m để hàm số y = f ( x ) 2 có đúng một điểm cực trị.
A. 1.
B. 4.
C. 2.
D. 3.
cho ham so f(x)=x^2-1. Tìm tất cả giá trị của x sao cho f(1-x) nhận giá trị âm
cho hàm số y = f(x)=2x^2 -5
a) tính f(-2), f(1),f(3)
b) tính giá trị của x để f(x)=3
c) tìm x thuộc z sao cho f(x) âm
a) Thay x=-2 vào hàm số \(f\left(x\right)=2x^2-5\),ta được:
\(f\left(-2\right)=2\cdot\left(-2\right)^2-5=2\cdot4-5=8-5=3\)
Thay x=1 vào hàm số \(f\left(x\right)=2x^2-5\), ta được:
\(f\left(1\right)=2\cdot1^2-5=2-5=-3\)
Thay x=3 vào hàm số \(f\left(x\right)=2x^2-5\), ta được:
\(f\left(3\right)=2\cdot3^2-5=2\cdot9-5=18-5=13\)
Vậy: f(-2)=3
f(1)=-3
f(3)=13
b) Để f(x)=3 thì \(2x^2-5=3\)
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=3 thì \(x\in\left\{2;-2\right\}\)
Đúng 2
Bình luận (1)
Cho hàm số f(x)
x
2
+ 2x − 3Xét các mệnh đề sau:i) f(x − 1)
x
2
− 4ii) Hàm số đã cho đồng biến trên (−1; +
∞
)iii) Giá trị nhỏ nhất của hàm số là một số âm.iv) Phương trình f(x) m có nghiệm khi m
≥
−4Số mệnh đề đúng là: A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Cho hàm số f(x) = x 2 + 2x − 3
Xét các mệnh đề sau:
i) f(x − 1) = x 2 − 4
ii) Hàm số đã cho đồng biến trên (−1; + ∞ )
iii) Giá trị nhỏ nhất của hàm số là một số âm.
iv) Phương trình f(x) = m có nghiệm khi m ≥ −4
Số mệnh đề đúng là:
A. 1
B. 2
C. 3
D. 4
Cho hàm số
f
(
x
)
x
3
–
(
2
m
-
1
)
x
2
+
(
2
-
m
)
x
+
2
. Tìm tất cả các giá trị thực của tham số m để hàm số yf(|x|) có 5 cực trị A.
-
10
m
5
4
B.
-...
Đọc tiếp
Cho hàm số f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tìm tất cả các giá trị thực của tham số m để hàm số y=f(|x|) có 5 cực trị
A. - 10 < m < 5 4
B. - 2 < m < 5
C. - 2 < m < 5 4
D. 5 4 < m < 2
Cho hàm số \(f\left(x\right)=x^2-1\).Tính các giá trị của x0 sao cho \(f\left(1-x_0\right)\)đạt giá trị âm.
Ta có: \(f\left(x\right)=x^2-1\)
\(\Rightarrow f\left(1-x_0\right)=\left(1-x_0\right)^2-1\)
\(=x_0^2-2x_0+1-1=x_0^2-2x_0\)
\(=x_0\left(x_0-2\right)\)
\(f\left(1-x_0\right)< 0\Leftrightarrow\)\(x_0\left(x_0-2\right)< 0\)
Mà \(x_0>x_0-2\)nên \(\hept{\begin{cases}x_0>0\\x_0-2< 0\end{cases}}\Leftrightarrow0< x_0< 2\)
Vậy \(0< x_0< 2\)thì \(f\left(1-x_0\right)\)đạt giá trị âm
Cho hàm số
f
(
x
)
l
n
2
(
x
2
-
2
x
+
5
)
.
Tìm các giá trị của x
f
(
x
)
0
.
A
.
x
≠
1
B
.
x
0
C...
Đọc tiếp
Cho hàm số f ( x ) = l n 2 ( x 2 - 2 x + 5 ) . Tìm các giá trị của x f ' ( x ) > 0 .
A . x ≠ 1
B . x > 0
C . m ọ i x ∈ R
D . x > 1
Cho hàm số y = 3x - 1 . Tìm các giá trị của x sao cho :
a) y nhận giá trị âm
b) y nhận giá trị lớn hơn 5
a) Để y nhận giá trị âm điều kiện là : 3x - 1 < 0 ↔ 3x < 1 ↔ x < \(\frac{1}{3}\)
Vậy với x < \(\frac{1}{3}\) thì y nhận giá trị âm
b) Để y nhận giá trị lớn hơn 5 điều kiện là : 3x - 1 > 5 ↔ 3x > 6 ↔ x > 2
Vậy với x > 2 thì y nhận giá trị lớn hơn 5
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
x
+
x
2
+
1
. Tập các giá trị của x để
2
x
.
f
(
x
)
-
f
(
x
)
≥
0
là: A.
1
3...
Đọc tiếp
Cho hàm số f ( x ) = x + x 2 + 1 . Tập các giá trị của x để 2 x . f ' ( x ) - f ( x ) ≥ 0 là:
A. 1 3 ; + ∞
B. - ∞ ; 1 3
C. [ 2 3 ; + ∞ )
D. [ 1 3 ; + ∞ )
Đáp án D
- Phương pháp: Sử dụng công thức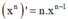 
và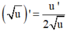 
tính f'(x). Từ đó giải bất phương trình.
- Cách giải:
+ Ta có: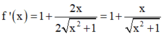 
+ Theo đề bài ta có: 2x.f'(x) - f(x) ≥ 0.
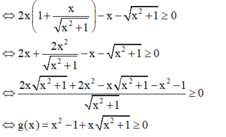
+ Thử các đáp án:
+ Với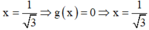 
thuộc tập nghiệm của BPT.
⇒ Loại đáp án A, B và C.
Đúng 0
Bình luận (0)