Cho hàm số thỏa mãn f(0) khác 0, f(1)=3
f(x).f(y) = f(x+y) + f(x-y) với mọi x, y thuộc Z
Tính f(7)
cho hàm số y=f(x) thỏa mãn: \(f\left(x\right)+3f\left(\frac{1}{x}\right)=x^2\) với mọi x khác 0. Tính f(2)
thay x=2 và x=1/2 ta có
\(\hept{\begin{cases}f\left(2\right)+3f\left(\frac{1}{2}\right)=4\\f\left(\frac{1}{2}\right)+3f\left(2\right)=\frac{1}{4}\end{cases}\Rightarrow f\left(2\right)=-\frac{13}{32}}\)
cho hàm số y=f(x) xác định với mọi x khác 0 thỏa mãn (x+1).f(x)+2.f(1/x)=x+3
tính f(1)
xét x=1:
=>(1+1).f(1)+2.f(1/1)=1+3
=>2.f(1)+2.f(1)=4
=>4.f(1)=4
=>f(1)=1
Vậy f(1)=1
Cho hàm số f(x) thỏa mãn f(xy+1) = f(x).f(y)- f(y) -x +2 đúng với mọi số nguyên x,y bất kì. Tính giá trị 10.f(2018) + f(0)
Xét x=0,y=1 ta có f(1)=f(0)f(1)-f(1)+2 (a)
xét x=1,y=0 ta có f(1)=f(1)f(0)-f(0)+1 (b)
xét x=0,y=0 ta có f(1)=f(0)f(0)-f(0)+2 (c)
Lấy (a)-(b) suy ra f(1)=f(0)+1 thay vào (c) ta được f(0)+1=f(0)f(0)-f(0)+2 <=>f(0).f(0)-2f(0)+1=0 <=> f(0)=1 =>f(1)=f(0)+1=2
xét x=1 ta có f(y+1)=f(1)f(y)-f(y)-1+2=f(y)+1
f(y+1)=f(y)+1=f(y-1)+1+1=...F(y-n)+1+n (n là số tự nhiên)
vậy f(2018)=f(2017+1)=f(2017-2016)+1+2016( lấy n=2016)=f(1)+2017=2019
vậy biểu thức có giá trị là 10.2019+1=20191
Cho hàm số y = f(x) có f’ (x) liên tục trên nửa khoảng [0;+∞) thỏa mãn biết 3f(x) + f(x) = 1 + 3 e - 2 x . Giá trị f(0) = 11 3 . Giá trị f 1 2 ln 6 bằng
A. 1 2
B. 5 6 18
C. 1
D. 5 6 9
Đáp án B
Phương pháp: Đạo hàm: ![]()
Cách giải:

![]()
![]()

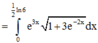
Ta có:
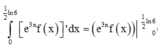

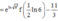
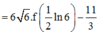


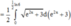
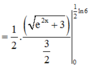
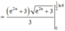
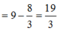
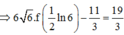
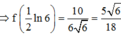
Cho hàm số y = f(x) xác định với mọi x thuộc z (x >0) và thỏa mãn f(1)=1, f(a+b)= f(a) +f(b) - 2f(ab).
Tính f(2014) và f(2015)
Cho hàm số y = f(x) xác định với mọi x thuộc z (x >0) và thỏa mãn f(1)=1, f(a+b)= f(a) +f(b) - 2f(ab).
Tính f(2014) và f(2015)
Cho hàm số y = f(x) xác định với mọi x thuộc z (x >0) và thỏa mãn f(1)=1, f(a+b)= f(a) +f(b) - 2f(ab).
Tính f(2014) và f(2015)
Cho hàm số y=f(x) xác định trên R và có đạo hàm f‘(x) thỏa mãn f’(x)=(1-x)(x+2).g(x) + 2018 trong đó g(x)<0, mọi x thuộc R. Hàm số y=f(1-x)+2018x+2019 nghịch biến trên khoảng nào?
![]()
![]()
![]()
![]()
Cho hàm số \(y=f\left(x\right)\)xác định với mọi x là số thực khác 0 thỏa mãn điều kiện \(f\left(x\right)+3f\left(\frac{1}{x}\right)=x^2\)
Tính f(2).
Tớ cảm ơn trước.
Thế \(x=2,x=\frac{1}{2}\)thì được
\(\hept{\begin{cases}f\left(2\right)+3f\left(\frac{1}{2}\right)=4\\f\left(\frac{1}{2}\right)+3f\left(2\right)=\frac{1}{4}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}f\left(2\right)=-\frac{13}{32}\\f\left(\frac{1}{2}\right)=\frac{47}{32}\end{cases}}\)