Em đăng mỗi lần 1 câu thôi thì mn sẽ giúp em nhanh hơn nhé!

Bài 16: 

a: Xét ΔOEH và ΔOFH có 

OE=OF

\(\widehat{EOH}=\widehat{FOH}\)

OH chung

Do đó: ΔOEH=ΔOFH

Bài 15:

a: Xét ΔABM và ΔACN có 

AB=AC

\(\widehat{NAC}\) chung

AM=AN

Do đó: ΔABM=ΔACN

b: Xét ΔNBC và ΔMCB có

NB=MC

\(\widehat{NBC}=\widehat{MCB}\)

BC chung

Do đó: ΔNBC=ΔMCB

Suy ra: \(\widehat{NCB}=\widehat{MBC}\)

hay \(\widehat{OBC}=\widehat{OCB}\)

lx

đâu vậy bạn

\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)

Ta lấy vễ trên chia vế dưới

\(=3.2=6\)

\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)

Ta lấy vế trên chia vế dưới

\(=2^3.3=24\)

\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)

\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}=3.2=6\)

\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)

ở chỗ 19?16 là em viết sai thật là 19/16 ạ

Mọi người trả lời nhanh giúp em với ạ

Giúp mik vs mik cung đang cân

\(\dfrac{9}{54}=\dfrac{1}{6}=\dfrac{4}{24}< \dfrac{7}{24}\)

\(\dfrac{7}{24}< \dfrac{12}{24}< \dfrac{16}{24}=\dfrac{2}{3}\)

\(\dfrac{2}{3}< \dfrac{2+1}{3+1}=\dfrac{3}{4}\)

\(\dfrac{3}{4}< \dfrac{3+2}{4+2}=\dfrac{5}{6}\)

\(\dfrac{5}{6}< \dfrac{5+2}{6+2}=\dfrac{7}{8}\)

\(\dfrac{7}{8}< \dfrac{7+9}{8+9}=\dfrac{16}{17}\)

Vậy \(\dfrac{9}{54}< \dfrac{7}{24}< \dfrac{2}{3}< \dfrac{3}{4}< \dfrac{5}{6}< \dfrac{7}{8}< \dfrac{16}{17}\)

9.

\(\Leftrightarrow a^2+a^2b^2+b^2+b^2c^2+c^2+c^2a^2\ge6abc\)

\(\Leftrightarrow\left(a^2-2abc+b^2c^2\right)+\left(b^2-2abc+c^2a^2\right)+\left(c^2-2abc+a^2b^2\right)\ge0\)

\(\Leftrightarrow\left(a-bc\right)^2+\left(b-ca\right)^2+\left(c-ab\right)^2\ge0\) (luôn đúng)

Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(0;0;0\right);\left(1;1;1\right);\left(1;-1;-1\right)\) và các hoán vị

10.

\(a^2+b^2+c^2=1\)

\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=1+2\left(ab+bc+ca\right)\)

\(\Leftrightarrow\left(a+b+c\right)^2=1+2\left(ab+bc+ca\right)\)

\(\Rightarrow1+2\left(ab+bc+ca\right)\ge0\Rightarrow ab+bc+ca\ge-\dfrac{1}{2}\)

Lại có:

\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)

\(\Leftrightarrow a^2+b^2+c^2\ge ab+bc+ca\)

\(\Rightarrow ab+bc+ca\le1\)

11.

Do \(a^2+b^2+c^2=1\Rightarrow\left\{{}\begin{matrix}\left|a\right|\le1\\\left|b\right|\le1\\\left|c\right|\le1\end{matrix}\right.\) \(\Rightarrow\left(a+1\right)\left(b+1\right)\left(c+1\right)\ge0\)

Do đó:

\(abc+2\left(1+a+b+c+ab+bc+ca\right)\)

\(=1+a+b+c+ab+bc+ca+\left(1+a+b+c+ab+bc+ca+abc\right)\)

\(=\dfrac{1}{2}\left(a^2+b^2+c^2\right)+ab+bc+ca+a+b+c+\dfrac{1}{2}+\left(a+1\right)\left(b+1\right)\left(c+1\right)\)

\(=\dfrac{1}{2}\left(a+b+c\right)^2+\left(a+b+c\right)+\dfrac{1}{2}+\left(a+1\right)\left(b+1\right)\left(c+1\right)\)

\(=\dfrac{1}{2}\left(a+b+c+1\right)^2+\left(a+1\right)\left(b+1\right)\left(c+1\right)\ge0\) (đpcm)

12.

\(a^4+3\ge4a\)

\(\Leftrightarrow a^4-2a^3+a^2+\left(2a^3-4a^2+2a\right)+\left(3a^2-6a+3\right)\ge0\)

\(\Leftrightarrow a^2\left(a-1\right)^2+2a\left(a-1\right)^2+3\left(a-1\right)^2\ge0\)

\(\Leftrightarrow\left(a^2+2a+3\right)\left(a-1\right)^2\ge0\)

\(\Leftrightarrow\left[\left(a+1\right)^2+2\right]\left(a-1\right)^2\ge0\) (luôn đúng)

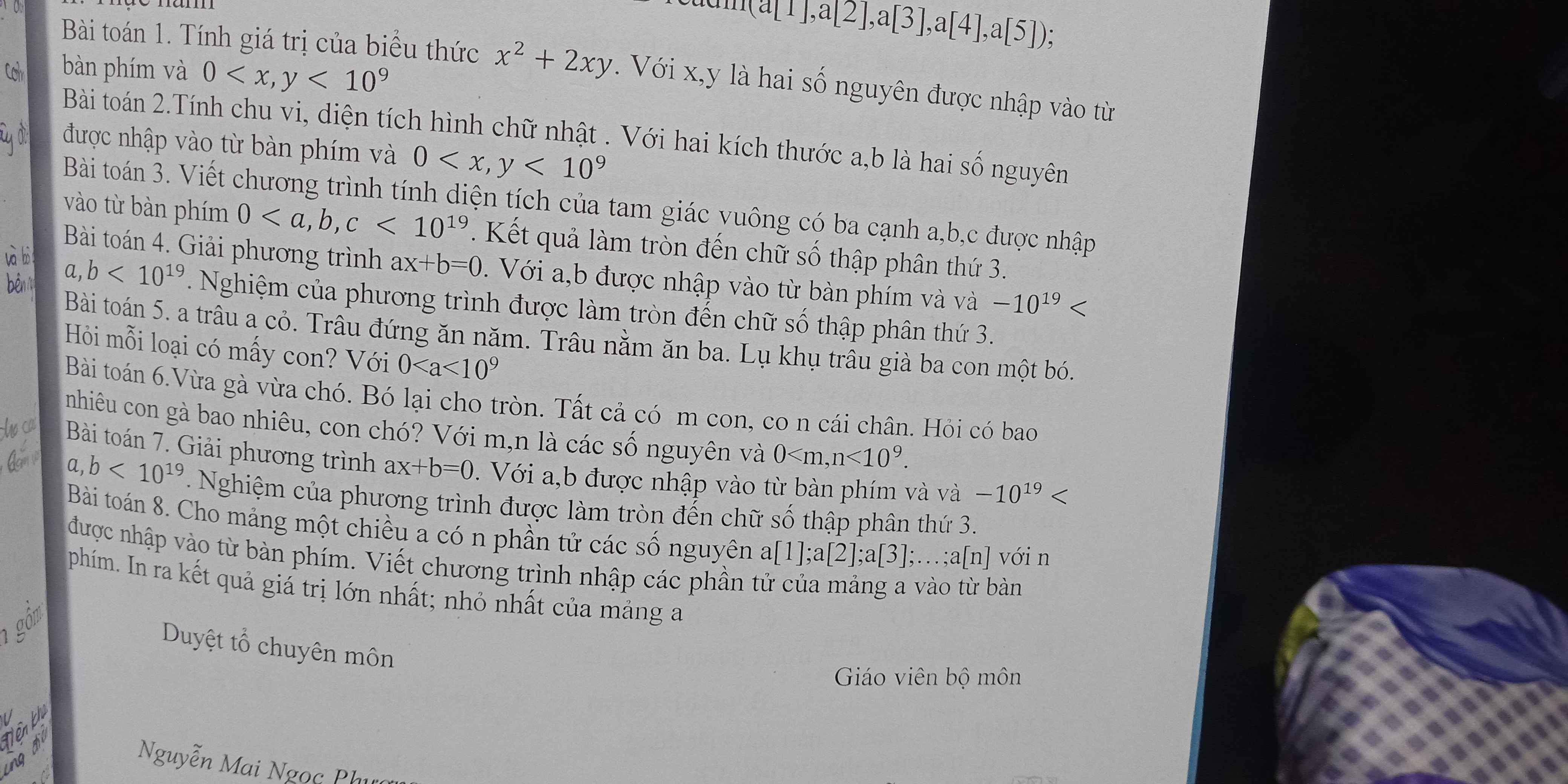
Bài 2: 

#include <bits/stdc++.h>

using namespace std;

long long a,b;

int main()

{

cin>>a>>b;

cout<<(a+b)*2<<endl;

cout<<a*b;

return 0;

}

64^10   -   32^11 - 16^13

=  (2^6)^10   -    (2^5)^11  -   (2^4)^13

= 2^60 - 2^55 - 2^52

= 2^52 ( 2^8 - 2^3 -1)

= 2^52 . 243

Vi 243 chia het cho 19 nen 2^52 . 243 chia het cho 9

Vay tong tren chia het cho 19