Chứng minh rằng số đo góc của n-giác đều là
\(\frac{\left(n-2\right).180^o}{n}\)
Những câu hỏi liên quan
Chứng minh rằng số đo góc của hình n - giác đều là \(\dfrac{\left(n-2\right).180^0}{n}\)
Điền vào chỗ trống trong các câu sau :
a) Biết rằng tổng số đo các góc của một đa giác n cạnh là widehat{A}_1+widehat{A}_2+widehat{A}_3+.....+widehat{A}_nleft(n-2right).180^0. Vậy tổng số đo các góc của một đa giác 7 cạnh là .......
b) Đa giác đều là đa giác có .....
c) Biết rằng số đo mỗi góc của một đa giác đều n cạnh là dfrac{left(n-2right).180^0}{n}, vậy :
Số đo mỗi góc của ngũ giác đều là ..............
Số đo mỗi góc của lục giác đều là ..............
Đọc tiếp
Điền vào chỗ trống trong các câu sau :
a) Biết rằng tổng số đo các góc của một đa giác n cạnh là \(\widehat{A}_1+\widehat{A}_2+\widehat{A}_3+.....+\widehat{A}_n=\left(n-2\right).180^0\). Vậy tổng số đo các góc của một đa giác 7 cạnh là .......
b) Đa giác đều là đa giác có .....
c) Biết rằng số đo mỗi góc của một đa giác đều n cạnh là \(\dfrac{\left(n-2\right).180^0}{n}\), vậy :
Số đo mỗi góc của ngũ giác đều là ..............
Số đo mỗi góc của lục giác đều là ..............
a) Tổng số đo các góc của một đa giác n cạnh = \((7-2).180^0\) = \(900^0\)
b)Số đo mỗi góc của ngũ giác đều là : \(\frac{(5-2).180^0}{5}\)= \(108^0\)
Số đo mỗi góc của lục giác đều là \(\frac{(6-2).180^0}{6}\)= \(120^0\)
Đúng 0
Bình luận (0)
a) Chứng minh tổng số đo các góc trong của một hình
n - giác là (n - 2)180°.
b) Tính tổng số đo các góc của một đa giác 12 cạnh.
a)Vẽ các đường chéo xuất phát từ một đỉnh của n - giác, ta được (n - 2) tam giác.
Tổng các góc của hình n - giác bằng tổng các góc của (n - 2) tam giác, tức là có số đo bằng (n - 2).1800.
b) ta có: (n - 2).1800 = (12 - 2 ).1800 = 18000
Đúng 0
Bình luận (0)
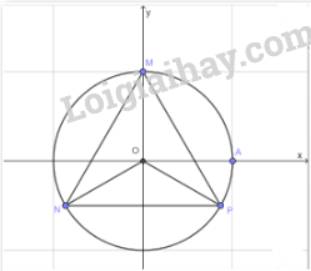
Gọi M, N, P là các điểm trên đường tròn lượng giác sao cho số đo của các góc lượng giác \(\left( {OA,OM} \right),\,\left( {OA,ON} \right),\,\left( {OA,OP} \right)\) lần lượt bằng \(\frac{\pi }{2};\,\,\frac{{7\pi }}{6};\,\, - \frac{\pi }{6}\). Chứng minh rằng tam giác MNP là tam giác đều.
Tham khảo:
\(\begin{array}{l}(OM,ON) = (OA,ON) - (OA,OM) = \frac{{2\pi }}{3}\\ \Rightarrow \widehat {MON} = {120^0}\\\widehat {MOP} = \widehat {MOA} + \widehat {AOP} = {90^0} + {30^0} = {120^0}\\ \Rightarrow \widehat {NOP} = {360^0} - {120^0} - {120^0} = {120^0}\end{array}\)
Cung MP = cung NP = cung NM
\(\Rightarrow MP = NP = NM\)
\(\Rightarrow \Delta MNP\) đều
Đúng 0
Bình luận (0)
Chứng minh công thức tính số tam giác trong tháp tam giác đều là: \(\frac{n\left(n+2\right)\left(2n+1\right)}{8}\)
công thức này sai ngay tầng một rồi còn chứng minh kiểu gì n=1 số tam giác là 9/8
Đúng 0
Bình luận (0)
Bài 1a. Nếu 3 đường thẳng cát nhau tại một điểm thì chúng tạo thành mấy cặp góc đối đỉnh( không kể góc bẹt )?b. Cũng hỏi như trên nếu thay 3 bằng n left(nin N;nge2right)Bài 2: Cho hai đường thẳng AB và CD cắt nhau tại O và tạo thành 4 góc(không kể góc bẹt)a. Chứng minh rằng trong các góc nói trên, tồn tại hai góc có số đo nhỏ hơn hoặc bằng 90^ob. Biết tổng số đo của 3 trong 4 góc trên là 225^o, tính số đo của mỗi gócBài 3: Chúng tỏ rằng hai tia phân giác của hai góc đối đỉnh là hai tia đối nhauB...
Đọc tiếp
Bài 1
a. Nếu 3 đường thẳng cát nhau tại một điểm thì chúng tạo thành mấy cặp góc đối đỉnh( không kể góc bẹt )?
b. Cũng hỏi như trên nếu thay 3 bằng n \(\left(n\in N;n\ge2\right)\)
Bài 2: Cho hai đường thẳng AB và CD cắt nhau tại O và tạo thành 4 góc(không kể góc bẹt)
a. Chứng minh rằng trong các góc nói trên, tồn tại hai góc có số đo nhỏ hơn hoặc bằng \(90^o\)
b. Biết tổng số đo của 3 trong 4 góc trên là \(225^o\), tính số đo của mỗi góc
Bài 3: Chúng tỏ rằng hai tia phân giác của hai góc đối đỉnh là hai tia đối nhau
Bài 4: Cho hai góc đối đỉnh. Vẽ tia phân giác của một trong hai góc đó. Chứng tỏ rằng tia đối của tia này là tia phân giác của góc còn lại
Bài 1. Chứng minh rằng với mọi số nguyên dương n thì 3^{n+2}-2^{n+2}+3^n-2^n.chia hết cho 10.Bài 2. Tìm x biếta) left|x-frac{1}{3}right|+frac{4}{5}left|left(-3,2right)+frac{2}{5}right|b) left(x-7right)^{x+1}-left(x-7right)^{x+11}0Bài 3. Số A chia thành ba số theo tỉ lệ frac{2}{5}:frac{3}{4}:frac{1}{6}Biết rằng tổng các bình phương của ba số đó bằng 24309. Tìm số A (Chú ý: số A chia thành 3 số nghĩa là 3 số được chia cộng lại bằng A).Bài 4. Cho tam giác ABC, M là trung điểm của BC. Trên tia đối c...
Đọc tiếp
Bài 1. Chứng minh rằng với mọi số nguyên dương n thì \(3^{n+2}-2^{n+2}+3^n-2^n.\)
chia hết cho 10.
Bài 2. Tìm x biết
a) \(\left|x-\frac{1}{3}\right|+\frac{4}{5}=\left|\left(-3,2\right)+\frac{2}{5}\right|\)
b) \(\left(x-7\right)^{x+1}-\left(x-7\right)^{x+11}=0\)
Bài 3. Số A chia thành ba số theo tỉ lệ \(\frac{2}{5}:\frac{3}{4}:\frac{1}{6}\)
Biết rằng tổng các bình phương của ba số đó bằng 24309. Tìm số A (Chú ý: số A chia thành 3 số nghĩa là 3 số được chia cộng lại bằng A).
Bài 4. Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của MA lấy E sao cho ME=MA. Chứng minh rằng:
a) AC=EB và AC song song với EB
b) Gọi I là điểm trên AC, K là một điểm trên EB sao cho AI=EK. Chứng minh I, M, K thẳng hàng.
c) Từ E kẻ EH vuông góc với BC (H thuộc BC). Biết góc HBE = 50 độ, góc MEB = 25 độ. Tính góc HEM, góc BME.
\(\text{Bn hỏi từ từ từng câu 1 thôi}\)
\(\text{Bn hỏi thế ai mà dám làm}\)
~~~~~~~~~~~~~
~~~~~~~~~~~
~~~~~~~~~~~~
Đúng 0
Bình luận (0)
Chí lí
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
sọ ghi 2 hàng khoogn đc tích tăng lê hiều hàng
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~````
Đúng 0
Bình luận (0)
Các bạn trả lời được câu nào thì trả lời câu đó, không nhất thiết phải tất cả
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
chứng minh rằng với mọi số tự nhiên n>1,ta đều có \(\frac{4^n}{n+1}< \frac{\left(2n\right)!}{\left(n!\right)^2}\)
Chứng minh rằng số đo của một hình n-giác đều là n - 2 . 180 0 n
Vẽ một n-giác lồi, kẻ các đường chéo xuất phát từ một đỉnh của n-giác lồi thì chia đa giác đó thành (n - 2) tam giác.
Tổng các góc của n-giác lồi bằng tổng các góc của (n - 2) tam giác bằng (n - 2).180o.
Hình n-gíác đều có n góc bằng nhau nên số đo mỗi góc bằng:
n - 2 . 180 0 n
Đúng 0
Bình luận (0)