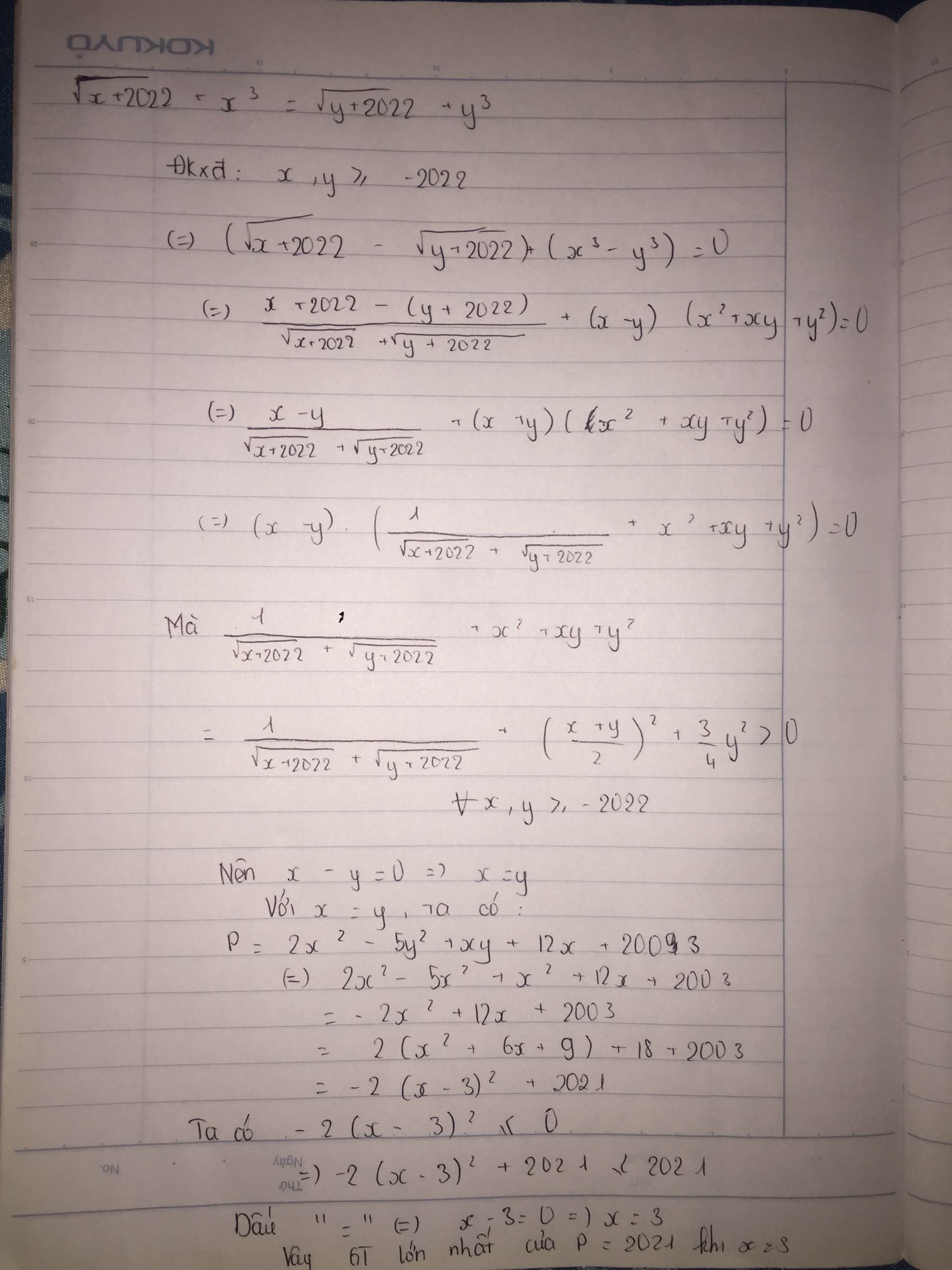tìm giá trị lớn nhất củaP =2x\(\sqrt{3-x^2}\) .

Những câu hỏi liên quan
Giá trị lớn nhất củaP=4x-x^2
Giá trị nhỏ nhất của P= x^2-4x+5
1;\(P=4x-x^2=-x^2+4x-4+4=-\left(x^2-4x+4\right)+4=-\left(x-2\right)^2+4\)
Có \(-\left(x-2\right)^2\le0\)
\(\Rightarrow P\le0+4=4\)
Vậy \(Max_P=4< =>x=2\)
2;\(P=x^2-4x+5=x^2-4x+4+1=\left(x-2\right)^2+1\ge1\)
Vậy \(MinP=1< =>x=2\)
Đúng 0
Bình luận (0)
tìm giá trị lớn nhất: \(A=3-\sqrt{x^2-2x}\)
đk x2 - 2x \(\ge\) 0 => x \(\in\) (-\(\infty\); 0] \(\cup\) [ 2; + \(\infty\))
\(\sqrt{x^2-2x}\) \(\ge\) 0
- \(\sqrt{x^2-2x}\) \(\le\) 0
A \(\le\) 3 => A(max) = 3 <=> x2 - 2x = 0 \(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Bài 1: Rút gọn biểu thức D sqrt{16x^4}-2x^2+1Bài 2: Tìm giá trị lớn nhất – nhỏ nhất của biểu thức sau : “ Dùng điều kiện xác định”e) E dfrac{2sqrt{x}}{sqrt{x}+3} ĐKXĐ: xge0Bài 3: Tìm giá trị lớn nhất – nhỏ nhất của biểu thức sau : “ Dùng hằng đẳng thức ”B 1-sqrt{x^2-2x+2}Bài 4: Cho P dfrac{4sqrt{x}+10}{2sqrt{x}-1}left(xge0;xnedfrac{1}{4}right). Tính tổng các giá trị x nguyên để biểu thức P có giá trị nguyên
Đọc tiếp
Bài 1: Rút gọn biểu thức D = \(\sqrt{16x^4}-2x^2+1\)
Bài 2: Tìm giá trị lớn nhất – nhỏ nhất của biểu thức sau : “ Dùng điều kiện xác định”
e) E = \(\dfrac{2\sqrt{x}}{\sqrt{x}+3}\) ĐKXĐ: \(x\ge0\)
Bài 3: Tìm giá trị lớn nhất – nhỏ nhất của biểu thức sau : “ Dùng hằng đẳng thức ”
B = \(1-\sqrt{x^2-2x+2}\)
Bài 4: Cho P = \(\dfrac{4\sqrt{x}+10}{2\sqrt{x}-1}\left(x\ge0;x\ne\dfrac{1}{4}\right)\). Tính tổng các giá trị x nguyên để biểu thức P có giá trị nguyên
Bài 1:
Ta có: \(D=\sqrt{16x^4}-2x^2+1\)
\(=4x^2-2x^2+1\)
\(=2x^2+1\)
Đúng 0
Bình luận (0)
tìm giá trị lớn nhất,giá trị nhỏ nhất của biểu thức sau:
a A= \(\sqrt{x-4}+\sqrt{5-x}\)
b B= \(\sqrt{3-2x}+\sqrt{3x+4}\)
Với các số thực không âm a; b ta luôn có BĐT sau:
\(\sqrt{a}+\sqrt{b}\ge\sqrt{a+b}\) (bình phương 2 vế được \(2\sqrt{ab}\ge0\) luôn đúng)
Áp dụng:
a.
\(A\ge\sqrt{x-4+5-x}=1\)
\(\Rightarrow A_{min}=1\) khi \(\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\)
\(A\le\sqrt{\left(1+1\right)\left(x-4+5-x\right)}=\sqrt{2}\) (Bunhiacopxki)
\(A_{max}=\sqrt{2}\) khi \(x-4=5-x\Leftrightarrow x=\dfrac{9}{2}\)
b.
\(B\ge\sqrt{3-2x+3x+4}=\sqrt{x+7}=\sqrt{\dfrac{1}{3}\left(3x+4\right)+\dfrac{17}{3}}\ge\sqrt{\dfrac{17}{3}}=\dfrac{\sqrt{51}}{3}\)
\(B_{min}=\dfrac{\sqrt{51}}{3}\) khi \(x=-\dfrac{4}{3}\)
\(B=\sqrt{3-2x}+\sqrt{\dfrac{3}{2}}.\sqrt{2x+\dfrac{8}{3}}\le\sqrt{\left(1+\dfrac{3}{2}\right)\left(3-2x+2x+\dfrac{8}{3}\right)}=\dfrac{\sqrt{510}}{6}\)
\(B_{max}=\dfrac{\sqrt{510}}{6}\) khi \(x=\dfrac{11}{30}\)
Đúng 3
Bình luận (0)
a)Ta có:A=\(\sqrt{x-4}+\sqrt{5-x}\)
=>A2=\(x-4+2\sqrt{\left(x-4\right)\left(5-x\right)}+5-x\)
=>A2= 1+\(2\sqrt{\left(x-4\right)\left(5-x\right)}\ge1\)
=>A\(\ge\)1
Dấu '=' xảy ra <=> x=4 hoặc x=5
Vậy,Min A=1 <=>x=4 hoặc x=5
Còn câu b tương tự nhé
Đúng 1
Bình luận (0)
Tìm giá trị lớn nhất của biểu thức : \(A=5+\sqrt{3+2x-x^2}\)
Cần gấp !!!
Cho \(\sqrt{x+2020}+x^3=\sqrt{y+2020}+y^3\) Tìm giá trị lớn nhất \(P=2x^2-5y^2+xy+12x+2003\)
P=\(\frac{x\sqrt{x}-2x-\sqrt{x}+2}{x\sqrt{x-3\sqrt{x}-2}}+\frac{x\sqrt{x}+2x-\sqrt{3}-2}{x\sqrt{x}-3\sqrt{x}+2}\\ \)
a)Rút gọn P, với giá trị nào của x thì P>1
b)Tìm x nguyên biết P đạt giá trị nguyên lớn nhất
cho A = \(\frac{3}{2+\sqrt{2x+3-x^2}}\)
a) Tìm x để A có nghĩa.
b) Tìm giá trị nhỏ nhất và giá trị lớn nhất của A.
a) Để A có nghĩa :
\(\Rightarrow\sqrt{2x+3-x^2\: }\Leftrightarrow2+\sqrt{2x+3-x^2}\ge2\forall x\)
\(\Rightarrow\sqrt{-\left(x-1\right)^2+4}\ge0\)
\(\Leftrightarrow-\left(x-1\right)^2\ge-4\)
\(\Leftrightarrow\left(x-1\right)^2\le4\)
\(\Rightarrow3\ge x\ge-1\)
Vậy.....
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất và giá trị nhỏ nhất, nếu cso
\(2x-3\sqrt(x)+7\)
\( 3-x+\sqrt(x)\)