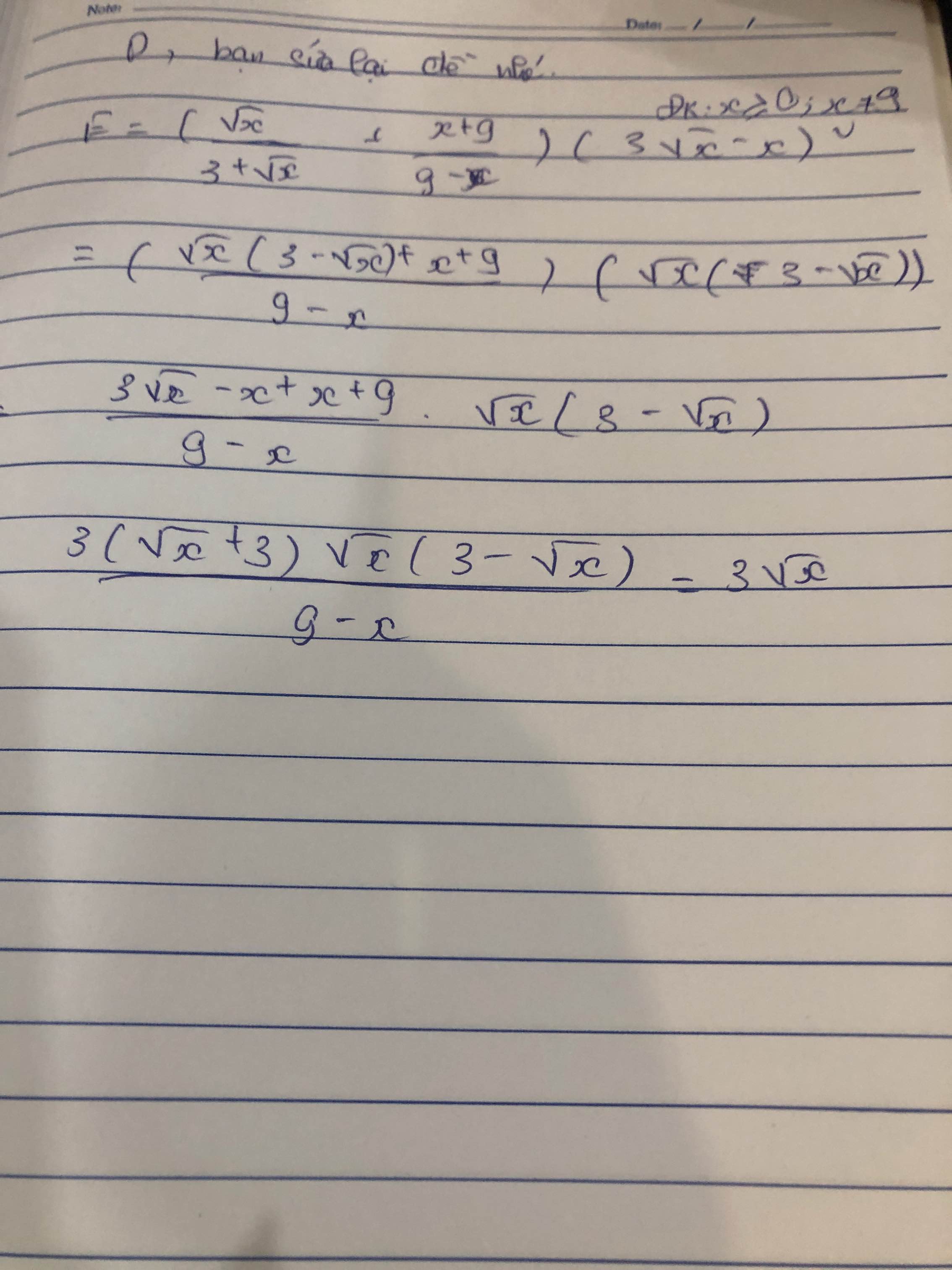4TTTT6 

gì v bn

a)\(=4\sqrt{6}-3\sqrt{6}+1-\sqrt{6}\)

\(=1\)

b)ĐK: \(x>0,x\ne9\)

\(=\left(\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)-x-9}{x-9}\right):\dfrac{3\sqrt{x}+1-\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}-3\right)}\)

\(=\dfrac{3\sqrt{x}-9}{\sqrt{x}+3}.\dfrac{\sqrt{x}}{2\sqrt{x}+4}\)

\(=\dfrac{3\sqrt{x}\left(\sqrt{x}-3\right)}{2\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)

6:ĐKXĐ: x>=0; x<>1/25

BPT=>\(\dfrac{3\sqrt{x}}{5\sqrt{x}-1}+3< =0\)

=>\(\dfrac{3\sqrt{x}+15\sqrt{x}-5}{5\sqrt{x}-1}< =0\)

=>\(\dfrac{18\sqrt{x}-5}{5\sqrt{x}-1}< =0\)

=>\(\dfrac{1}{5}< \sqrt{x}< =\dfrac{5}{18}\)

=>\(\dfrac{1}{25}< x< =\dfrac{25}{324}\)

7:

ĐKXĐ: x>=0

BPT \(\Leftrightarrow\dfrac{\sqrt{x}+1}{2\sqrt{x}+3}>\dfrac{8}{3}:\dfrac{8}{3}=1\)

=>\(\dfrac{\sqrt{x}+1}{2\sqrt{x}+3}-1>=0\)

=>\(\dfrac{\sqrt{x}+1-2\sqrt{x}-3}{2\sqrt{x}+3}>=0\)

=>\(-\sqrt{x}-2>=0\)(vô lý)

8:

ĐKXĐ: x>=0; x<>9/4

BPT \(\Leftrightarrow\dfrac{\sqrt{x}-2}{2\sqrt{x}-3}+4< 0\)

=>\(\dfrac{\sqrt{x}-2+8\sqrt{x}-12}{2\sqrt{x}-3}< 0\)

=>\(\dfrac{9\sqrt{x}-14}{2\sqrt{x}-3}< 0\)

TH1: 9căn x-14>0 và 2căn x-3<0

=>căn x>14/9 và căn x<3/2

=>14/9<căn x<3/2

=>196/81<x<9/4

TH2: 9căn x-14<0 và 2căn x-3>0

=>căn x>3/2 hoặc căn x<14/9

mà 3/2<14/9

nên trường hợp này Loại

9: 

ĐKXĐ: x>=0

\(BPT\Leftrightarrow\dfrac{2\sqrt{x}+3}{5\sqrt{x}+7}< =-\dfrac{1}{3}\)

=>\(\dfrac{2\sqrt{x}+3}{5\sqrt{x}+7}+\dfrac{1}{3}< =0\)

=>\(\dfrac{6\sqrt{x}+9+5\sqrt{x}+7}{3\left(5\sqrt{x}+7\right)}< =0\)

=>\(\dfrac{11\sqrt{x}+16}{3\left(5\sqrt{x}+7\right)}< =0\)(vô lý)

10: 

ĐKXĐ: x>=0; x<>1/49

\(BPT\Leftrightarrow\dfrac{6\sqrt{x}-2}{7\sqrt{x}-1}+6>0\)

=>\(\dfrac{6\sqrt{x}-2+42\sqrt{x}-6}{7\sqrt{x}-1}>0\)

=>\(\dfrac{48\sqrt{x}-8}{7\sqrt{x}-1}>0\)

=>\(\dfrac{6\sqrt{x}-1}{7\sqrt{x}-1}>0\)

TH1: 6căn x-1>0 và 7căn x-1>0

=>căn x>1/6 và căn x>1/7

=>căn x>1/6

=>x>1/36

TH2: 6căn x-1<0 và 7căn x-1<0

=>căn x<1/6 và căn x<1/7

=>căn x<1/7

=>0<=x<1/49

Đặt:\(\sqrt{x+9}=v;\sqrt{x+6}=u\)

Ta có: \(v+5u=5+vu\Leftrightarrow-v\left(u-1\right)+5\left(u-1\right)\Leftrightarrow\left(5-v\right)\left(u-1\right)\)

\(\left\{{}\begin{matrix}5-v=0\Leftrightarrow5=\sqrt{x+9}\Leftrightarrow x=16\left(N\right)\\u-1=0\Leftrightarrow\sqrt{x+6}=1\Leftrightarrow x=-5\left(N\right)\end{matrix}\right.ĐKXĐ:x>=-6\)

\(S=\left\{16,-5\right\}\)

Câu trên mình quên -5>-6

Đặt: \(\sqrt{x+9}=v;\sqrt{x+6}=u\)

Ta có: \(v+5u=5+vu\)

\(\Leftrightarrow v+5u-5-uv=0\)

\(\Leftrightarrow-v\left(u-1\right)+5\left(u-1\right)\)

\(\Leftrightarrow\left(5-v\right)\left(u-1\right)\)

\(\left\{{}\begin{matrix}5-v=0\Leftrightarrow5=\sqrt{x+9}\Leftrightarrow x=16\left(N\right)\\u-1=0\Leftrightarrow\sqrt{x+6}=1\Leftrightarrow x=-5\left(L\right)\end{matrix}\right.\)          ĐKXĐ:\(x>=-6\)

\(S=\left\{16\right\}\)

\(\sqrt{x+9}+5\sqrt{x+\text{6}}=5+\sqrt{\left(x+9\right)\left(x+\text{6}\right)}\Leftrightarrow\sqrt{x+9}+5=5+\sqrt{x+9}\Leftrightarrow\sqrt{x+9}-\sqrt{x+9}=0\Leftrightarrow x+9-x-9=0\Leftrightarrow0=0\)

Vậy x vô số nghiệm

11111111

Đk : x >= 9

pt <=> \(\sqrt{\left(x-9\right)+6\sqrt{x-9}+9}\)+    \(\sqrt{\left(x-9\right)-6\sqrt{x-9}+9}\)-   1 = 0

<=> \(\sqrt{\left(\sqrt{x-9}+3\right)^2}\)+    \(\sqrt{\left(\sqrt{x-9}-3\right)^2}\)-    1 = 0

<=> \(\sqrt{x-9}+3\)+  |\(\sqrt{x-9}\)-  3|   -   1 = 0

Đến đó bạn xét 2 trường hợp đề loại dấu "| |" để giải pt nha

Tk mk 

a) \(\dfrac{3-\sqrt{x}}{x-9}=\dfrac{-\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=-\dfrac{1}{\sqrt{x+3}}\)(\(x\ge0,x\ne9\))

b) \(\dfrac{x-5\sqrt{x}+6}{\sqrt{x}-3}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\sqrt{x}-3}=\sqrt{x}-2\left(x\ge0,x\ne9\right)\)

a) \(\dfrac{3-\sqrt{x}}{x-9}=\dfrac{3-\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=-\dfrac{1}{\sqrt{x}+3}\)

b) \(\dfrac{x-5\sqrt{x}+6}{\sqrt{x}-3}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}{\sqrt{x}-3}=\sqrt{x}-2\)

c) \(6-2x-\sqrt{9-6x+x^2}=6-2x-\sqrt{\left(3-x\right)^2}=6-2x-\left|3-x\right|\)

mà \(x< 3\Rightarrow3-x>0\Rightarrow6-2x-\left|3-x\right|=6-2x-3+x=3-x\)

a,\(\dfrac{3-\sqrt{x}}{x-9}\)

=\(-\dfrac{3-\sqrt{x}}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\)

=\(-\dfrac{1}{3+\sqrt{x}}\)

\(a,\dfrac{-5}{x+6}\ge0\\ mà\left(-5< 0\right)\\ \Rightarrow x+6< 0\\ \Rightarrow x< -6\\ b,\dfrac{2}{6-x}\ge0\\ mà\left(2>0\right)\\ \Rightarrow6-x>0\\ \Rightarrow x< 6\\ c,\dfrac{-x+3}{-6}\ge0\\ mà-6< 0\\ \Rightarrow-x+3< 0\\ \Rightarrow x>3\\\)

\(d,\dfrac{7x-1}{-9}\ge0\\mà-9< 0\\ \Rightarrow 7x-1\le0\\ \Rightarrow x\le\dfrac{1}{7}\\ e,\dfrac{x+2}{x^2+2x+1}\ge0\\ mà\left(x^2+2x+1\right)>0\forall x\\ \Rightarrow x+2\ge0\\ \Rightarrow x\ge-2\\ f,\dfrac{x-2}{x^2-2x+4}\ge0\\ mà\left(x^2-2x+4\right)>0\forall x\\ \Rightarrow x-2\ge0\\ \Rightarrow x\ge2\)

Chứng minh : \(x^2-2x+4>0\\ x^2-2x+1+3=\left(x-1\right)^2+3\ge3>0\)

a: ĐKXĐ: \(\dfrac{-5}{x+6}>=0\)

=>x+6<0

=>x<-6

b: ĐKXĐ: (-2)/(6-x)>=0

=>6-x<0

=>x>6

c: ĐKXĐ: (-x+3)/(-6)>=0

=>-x+3<=0

=>-x<=-3

=>x>=3

d: ĐKXĐ: (7x-1)/-9>=0

=>7x-1<=0

=>x<=1/7

e: ĐKXĐ: (x+2)/(x^2+2x+1)>=0

=>x+2>=0

=>x>=-1

f: ĐKXĐ: (x-2)/(x^2-2x+4)>=0

=>x-2>=0

=>x>=2

ĐK: \(x\ge9\)

\(P=\sqrt{x-9+6\sqrt{x-9}+9}+\sqrt{x-9-6\sqrt{x-9}+9}\)

\(P=\sqrt{\left(\sqrt{x-9}+3\right)^2}+\sqrt{\left(\sqrt{x-9}-3\right)^2}\)

\(P=\left|\sqrt{x-9}+3\right|+\left|\sqrt{x-9}-3\right|\)

\(\Rightarrow P\ge\left|\sqrt{x-9}+3+3-\sqrt{x-9}\right|=6\)

\(\Rightarrow P_{min}=6\) khi \(\sqrt{x-9}\le3\Rightarrow9\le x\le18\)

@Nguyễn Việt Lâm