Giúp mình gaiir câu 21 22 nhanh với ạ

Những câu hỏi liên quan
Làm dùm mình từ câu 1 đến 20 với ạ.
GIẢI THÍCH CHI TIẾT DÙM MÌNH VỚI Ạ 

Giúp mik gaiir câu 24 đến 38 đi ạ 
24. Admission
28. memorialize
32. announcements
33. production
34. winner
38. sportsmanship
Đúng 1
Bình luận (0)
Câu 21 với 22 giúp mình với ạ 
21.
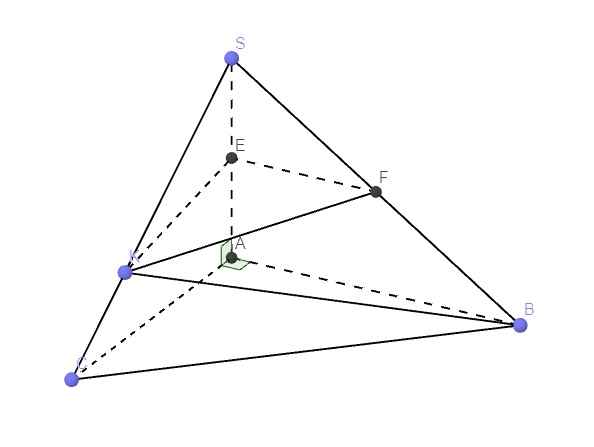
\(\left\{{}\begin{matrix}SA\perp AB\\AC\perp AB\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAC\right)\)
E là trung điểm SA, F là trung điểm SB \(\Rightarrow\) EF là đường trung bình tam giác SAB
\(\Rightarrow EF||AB\Rightarrow EF\perp\left(SAC\right)\)
\(\Rightarrow EF=d\left(F;\left(SEK\right)\right)\)
\(SE=\dfrac{1}{2}SA=\dfrac{3a}{2}\) ; \(EF=\dfrac{1}{2}AB=a\)
\(SC=\sqrt{SA^2+AC^2}=a\sqrt{13}\Rightarrow SK=\dfrac{2}{3}SC=\dfrac{2a\sqrt{13}}{3}\)
\(\Rightarrow S_{SEK}=\dfrac{1}{2}SE.SK.sin\widehat{ASC}=\dfrac{1}{2}.\dfrac{3a}{2}.\dfrac{2a\sqrt{13}}{3}.\dfrac{2a}{a\sqrt{13}}=a^2\)
\(\Rightarrow V_{S.EFK}=\dfrac{1}{3}EF.S_{SEK}=\dfrac{1}{3}.a.a^2=\dfrac{a^3}{3}\)
\(AB\perp\left(SAC\right)\Rightarrow AB\perp\left(SEK\right)\Rightarrow AB=d\left(B;\left(SEK\right)\right)\)
\(\Rightarrow V_{S.EBK}=\dfrac{1}{3}AB.S_{SEK}=\dfrac{1}{3}.2a.a^2=\dfrac{2a^3}{3}\)
Đúng 1
Bình luận (0)
22.
Gọi D là trung điểm AB
Do tam giác ABC đều \(\Rightarrow CD\perp AB\Rightarrow CD\perp\left(SAB\right)\)
\(\Rightarrow CD=d\left(C;\left(SAB\right)\right)\)
\(CD=\dfrac{AB\sqrt{3}}{2}=a\sqrt{3}\) (trung tuyến tam giác đều)
N là trung điểm SC \(\Rightarrow d\left(N;\left(SAB\right)\right)=\dfrac{1}{2}d\left(C;\left(SAB\right)\right)=\dfrac{a\sqrt{3}}{2}\)
\(S_{SAB}=\dfrac{1}{2}SA.AB=a^2\sqrt{3}\) \(\Rightarrow S_{SAM}=\dfrac{1}{2}S_{SAB}=\dfrac{a^2\sqrt{3}}{2}\)
\(\Rightarrow V_{SAMN}=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}.\dfrac{a^2\sqrt{3}}{2}=\dfrac{a^3}{4}\)
Lại có:
\(V_{SABC}=\dfrac{1}{3}SA.S_{ABC}=\dfrac{1}{3}.a\sqrt{3}.\dfrac{\left(2a\right)^2\sqrt{3}}{4}=a^3\)
\(\Rightarrow V_{A.BCMN}=V_{SABC}-V_{SANM}=\dfrac{3a^3}{4}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Các bạn ơi giúp mình với ạ mình cảm ơn các bạn rất nhìu mai mình nộp rồi giải nhanh giúp mình với ạ 🥺 Bài 1 cho tổng S=2+2²+2³.....+2²⁰¹⁰ Chứng minh rằng a S chia hết cho 15 b S chia hết cho 21 c S chia hết cho 35 d S chia hết cho 105 Bài 2 cho tổng A=12+18+24+x với x thuộc Z Tìm x để : a A chia hết cho 2 b A chia hết cho 3 mình cảm ơn nhiều ạ 😁
Bầi 2:
a: A=x+54
Để A chia hết cho 2 thì x chia hết cho 2
b: Để A chia hết cho 3 thì x chia hết cho 3
Đúng 0
Bình luận (1)
Giúp mình giải chi tiết câu 3 với 4 nhanh với ạ
3.
\(\overrightarrow{AB}=\left(4;2\right)=2\left(2;1\right)\)
Do đó đường thẳng AB nhận \(\left(-1;2\right)\) là 1 vtpt
4.
\(\overrightarrow{AB}=\left(-a;b\right)\)
\(\Rightarrow\) Đường thẳng AB nhận (b;a) là 1 vtpt
Đúng 0
Bình luận (0)
Giúp mình giải bài này với!
Chứng minh:
11;15 <1:21+1:22+1:23+..........+1:60<3:2
Ta có: A=1/21 + 1/22 + 1/23 + ... + 1/60
A= (1/21 + 1/22 + ... + 1/40) + (1/41 + 1/42 + ... + 1/60)
A < 1/20 * 20 + 1/40 * 20 = 1 + 1/2 = 3/2
Lại có: A = (1/21 + 1/22 + ... +1/40) + (1/41+ 1/42 + ... +1/60)
A > 1/40*20 + 1/60 * 20 = 1/2 + 1/3 = 5/6 > 11/15
==> 11/15 < 1/21 + 1/22 + ... + 1/60 < 3/2
Ta có: A=1/21 + 1/22 + 1/23 + ... + 1/60
A= (1/21 + 1/22 + ... + 1/40) + (1/41 + 1/42 + ... + 1/60)
A < 1/20 * 20 + 1/40 * 20 = 1 + 1/2 = 3/2
Lại có: A = (1/21 + 1/22 + ... +1/40) + (1/41+ 1/42 + ... +1/60)
A > 1/40*20 + 1/60 * 20 = 1/2 + 1/3 = 5/6 > 11/15
==> 11/15 < 1/21 + 1/22 + ... + 1/60 < 3/2
Xem thêm câu trả lời
Giúp e làm chi tiết câu 21, 22 đi ạ
21.
Giới hạn đã cho hữu hạn khi và chỉ khi \(a=1\)
Khi đó:
\(\lim\limits_{x\rightarrow+\infty}\left(x-\sqrt{x^2+bx+2}\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{x^2-\left(x^2+bx+2\right)}{x+\sqrt{x^2+bx+2}}=\lim\limits_{x\rightarrow+\infty}\dfrac{-bx-2}{x+\sqrt{x^2+bx+2}}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{-b-\dfrac{2}{x}}{1+\sqrt{1+\dfrac{b}{x}+\dfrac{2}{x^2}}}=\dfrac{-b}{2}\)
\(\Rightarrow-\dfrac{b}{2}=4\Rightarrow b=-8\)
\(\Rightarrow a+b=1-8=-7\)
22.
B sai, do các cạnh bên của chóp đều tạo với đáy các góc bằng nhau
Đúng 0
Bình luận (0)
Chỉ dùm mình câu 17 với ạ.
the people who are unable to see (những người không thể nhìn) = the blind (người mù nói chung)
Đúng 1
Bình luận (0)
Giúp mình giải câu 9 câu 10 nhanh với ạ
9.
Phương trình đường thẳng AB: \(3x-y-7=0\)
Trung điểm đoạn thẳng AB: \(I=\left(2;-1\right)\)
Trung trực đoạn AB vuông góc với AB có phương trình dạng: \(\left(\Delta\right):x+3y+m=0\)
Mà I thuộc \(I\in\Delta\Rightarrow2-3+m=0\Leftrightarrow m=1\)
\(\Rightarrow\Delta:x+3y+1=0\)
Đúng 1
Bình luận (0)
10.
Phương trình đường thẳng AB: \(y+4=0\)
Trung điểm đoạn thẳng AB: \(I=\left(2;-4\right)\)
Trung trực đoạn AB vuông góc với AB có phương trình dạng: \(\left(\Delta\right):x+m=0\)
Mà I thuộc \(I\in\Delta\Rightarrow2+m=0=0\Leftrightarrow m=-2\)
\(\Rightarrow\Delta:x-2=0\)
Đúng 0
Bình luận (0)