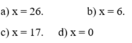a) 12+(2x-11)=53

(2x-11) = 53-12

2x-11= 41

2x=41+11

2x=52

x= 52:2

x=26

Vậy...

\(b,21-\left(-6+3x\right)=9\)

\(\Rightarrow21+6-3x=9\)

\(\Rightarrow27-3x=9\)

\(\Rightarrow3x=18\)

\(\Rightarrow x=6\)

c, -(2x+4)+11=-27

=>-2x-4+11=-27

=>-2x+7=-27

=>-2x = -34

=>x=17

d, 33-(33-x)=0

=>33-33+x=0

=>x=0

\(2x=3y=5z\Rightarrow\frac{2x}{30}=\frac{3y}{30}=\frac{5z}{30}\Rightarrow\frac{x}{15}=\frac{y}{10}=\frac{z}{6}\)

\(\Rightarrow\frac{x}{15}=\frac{y}{10}=\frac{z}{6}=\frac{x-y+z}{15-10+6}=\frac{-33}{11}=-3\)

\(\Rightarrow\hept{\begin{cases}x=-3.15=-45\\y=-3.10=-30\\z=-3.6=-18\end{cases}}\)

Vậy \(x=-45\), \(y=-30\), \(z=-18\).

Ta có:

2x=3y=5z=>\(\frac{2x}{30}=\frac{3y}{30}=\frac{5y}{30}\)=>\(\frac{x}{15}=\frac{y}{10}=\frac{z}{6}\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\frac{x}{15}=\frac{y}{10}=\frac{z}{6}=\frac{x-y+z}{15-10+6}=\frac{-33}{9}=\frac{-11}{3}\)

=>\(\frac{x}{15}=\frac{-11}{3}\)=>\(x=\frac{-11}{3}.15=-55\)

    \(\frac{y}{10}=\frac{-11}{3}\)=>\(y=\frac{-11}{3}.10=\frac{-110}{3}\)

     \(\frac{z}{6}=\frac{-11}{3}\)=>\(z=-\frac{11}{3}.6=-22\)

Vậy

x,y nguyên không bạn

Ta có: x y − 3 x − 2 y = 16 x 2 + y 2 − 2 x − 4 y = 33 1

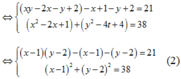
Đặt u = x − 1 , v = y − 2 ta được h

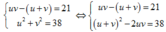
Đặt S = u + v, P = uv ta được hệ P − S = 21 S 2 − 2 P = 38 ⇔ P = S + 21 S 2 − 2 S − 80 = 0

⇔ S = − 8 P = 13 hoặc S = 10 P = 31

+ Khi ⇔ S = − 8 P = 13 thì u, v là nghiệm của phương trình X 2 + 8 X + 13 = 0

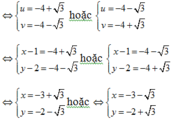
+ Khi S = 10 P = 31 thì u, v là nghiệm của phương trình X 2 - 10 X + 31 = 0 (vô nghiệm)

Vậy hệ có nghiệm  x ; y = − 3 − 3 ; − 2 + 3    x ; y = − 3 + 3 ; − 2 − 3

Đáp án cần chọn là: A

Đăng từng câu đio

,(8x-3).(3x+2)-(4x+7).(x+4)=(2x+1).(5x-1)-33 đúng không bạn

\(\Rightarrow\left(\dfrac{33}{11}\right)^{2x}=81\Rightarrow3^{2x}=3^4\Rightarrow x=2\)

\(A=-x^2-y^2+xy+2x+2y\\ =-2x^2-2y^2+2xy+4x+4y\\ =\left(-x^2+2xy-y^2\right)+\left(-x^2+4x-4\right)+\left(-y^2+4y-4\right)+8\\ =-\left(x^2-2xy+y^2\right)-\left(x^2-4x+4\right)-\left(y^2-4y+4\right)+8\\ =-\left(x-y\right)^2-\left(x-2\right)^2-\left(y-2\right)^2+8\\ =-\left[\left(x-y\right)^2+\left(x-2\right)^2+\left(y-2\right)^2\right]+8\\ \left(x-y\right)^2\ge0\forall x,y;\left(x-2\right)^2\ge0\forall x;\left(y-2\right)^2\ge0\forall y\\ \Rightarrow\left(x-y\right)^2+\left(x-2\right)^2+\left(y-2\right)^2\ge0\\ \Leftrightarrow-\left[\left(x-y\right)^2+\left(x-2\right)^2+\left(y-2\right)^2\right]\le0\\ \Leftrightarrow-\left[\left(x-y\right)^2+\left(x-2\right)^2+\left(y-2\right)^2\right]+8\le8\)

Dấu "=" xảy ra khi:

\(\left\{{}\begin{matrix}\left(x-y\right)^2=0\\\left(x-2\right)^2=0\\\left(y-2\right)^2=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x-y=0\\x-2=0\\y-2=0\end{matrix}\right.\\ \Leftrightarrow x=y=2\)

Vậy \(MAX_A=8\text{ khi }x=y=2\)

Đề là: \(P=x^3+y^3-\dfrac{x^2+y^2}{\left(x-1\right)\left(y-1\right)}\)

Hay \(P=\dfrac{x^3+y^3-\left(x^2+y^2\right)}{\left(x-1\right)\left(y-1\right)}\) 

Cái nào em nhỉ?

\(P=\dfrac{x^3+y^3-\left(x^2+y^2\right)}{\left(x-1\right)\left(y-1\right)}=\dfrac{x^3-x^2+y^3-y^2}{\left(x-1\right)\left(y-1\right)}=\dfrac{x^2\left(x-1\right)+y^2\left(y-1\right)}{\left(x-1\right)\left(y-1\right)}\)

\(P=\dfrac{x^2}{y-1}+\dfrac{y^2}{x-1}\)

Ta có:

\(\dfrac{x^2}{y-1}+4\left(y-1\right)\ge2\sqrt{\dfrac{4x^2\left(y-1\right)}{y-1}}=4x\)

Tương tự: \(\dfrac{y^2}{x-1}+4\left(x-1\right)\ge4y\)

Cộng vế:

\(P+4\left(x+y\right)-8\ge4\left(x+y\right)\)

\(\Rightarrow P\ge8\)

\(P_{min}=8\) khi \(x=y=2\)