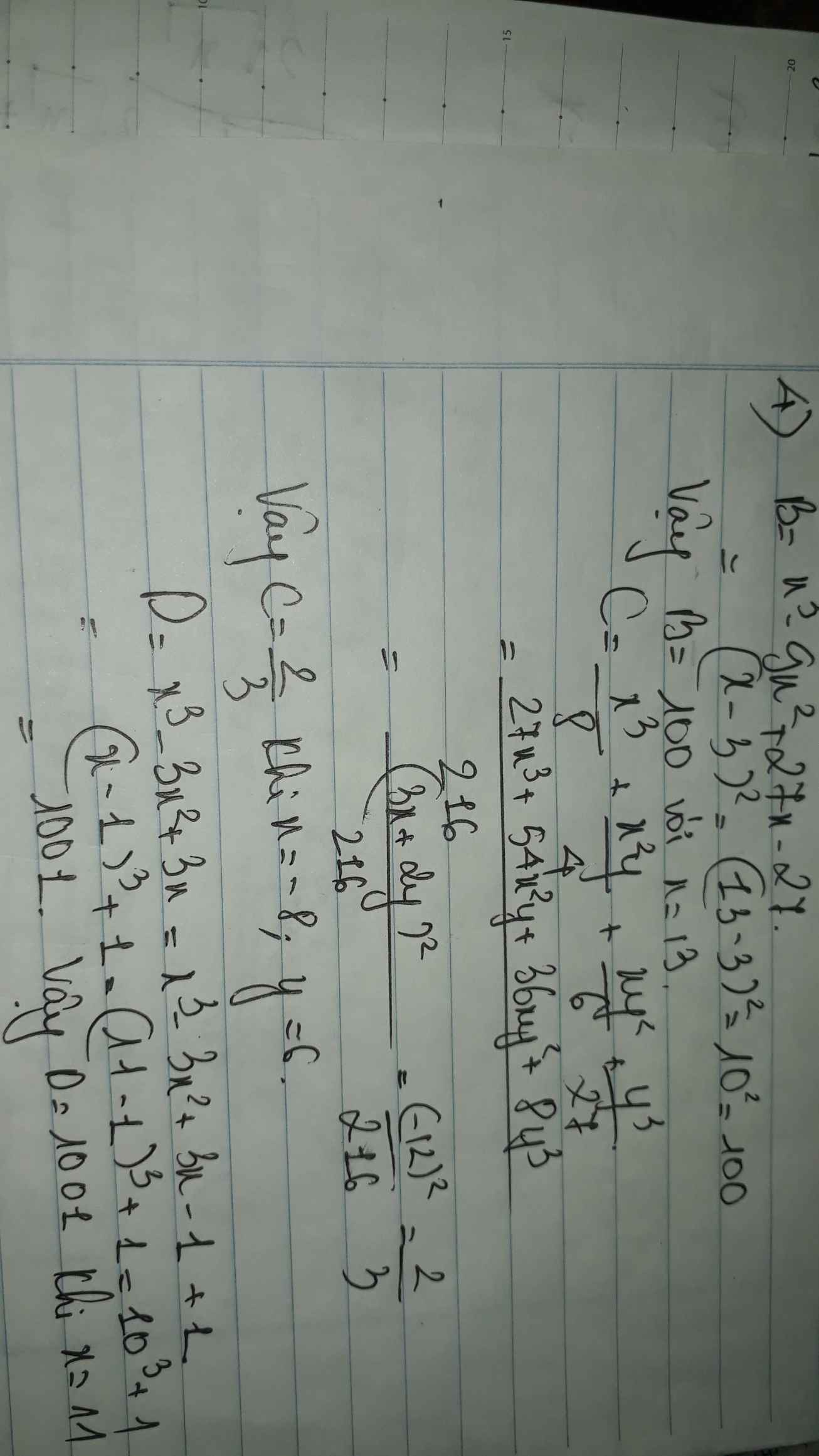Giúp mình câu c d bài hình với ạ :((

Những câu hỏi liên quan
Giải giúp mình bài hình câu c , d với ạ
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
Đọc tiếp
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Đúng 4
Bình luận (0)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
Đúng 1
Bình luận (0)
Giúp mình làm Câu c) bài hình và bài cuối với ạ, mình cảm ơn :3
Nhanh một chút ạ, mình đang cần

Câu 4:
D và F cùng nhìn AC dưới 1 góc vuông nên tứ giác ACDF nội tiếp
\(\Rightarrow\widehat{ADF}=\widehat{ACF}\) (cùng chắn AF)
Tương tự, ABDE nội tiếp \(\Rightarrow\widehat{ABE}=\widehat{ADE}\) (cùng chắn AE)
Lại có \(\widehat{ABE}=\widehat{ACF}\) (cùng phụ góc \(\widehat{A}\))
\(\Rightarrow\widehat{ADE}=\widehat{ADF}\) hay AD là phân giác góc \(\widehat{FDE}\)
./
Hoàn toàn tương tự, ta cũng có CF là phân giác \(\widehat{DFE}\Rightarrow\widehat{BFD}=\widehat{AFE}\)
Mà \(\widehat{AFE}=\widehat{BFK}\Rightarrow\widehat{BFK}=\widehat{BFD}\)
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{FK}{FD}\) theo định lý phân giác
Đồng thời \(\dfrac{CK}{CD}=\dfrac{FK}{FD}\) (CF là phân giác ngoài góc \(\widehat{DFK}\))
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{CK}{CD}\Rightarrow\dfrac{BK}{CK}=\dfrac{BD}{CD}\)
Qua B kẻ đường thẳng song song AC cắt AK và AD tại P và Q
Theo Talet: \(\dfrac{BK}{CK}=\dfrac{BP}{AC}\) đồng thời \(\dfrac{BD}{DC}=\dfrac{BQ}{AC}\)
\(\Rightarrow\dfrac{BP}{AC}=\dfrac{BQ}{AC}\Rightarrow BP=BQ\)
Mặt khác BP song song MF (cùng song song AC)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{AF}{AB}\) ; \(\dfrac{NF}{BQ}=\dfrac{AF}{AB}\) (Talet)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{NF}{BQ}\Rightarrow MF=NF\)
Đúng 1
Bình luận (3)
Câu 5:
ĐKXĐ: \(-1\le x\le1\)
Đặt \(\sqrt{1+x}+\sqrt{1-x}=t>0\)
\(\Rightarrow t^2=1+x+1-x+2\sqrt{\left(1+x\right)\left(1-x\right)}=2+2\sqrt{1-x^2}\)
Do đó pt trở thành:
\(t.t^2=8\Leftrightarrow t^3=8\)
\(\Leftrightarrow t=2\Leftrightarrow\sqrt{1-x}+\sqrt{1+x}=2\)
\(\Leftrightarrow2+2\sqrt{1-x^2}=4\Leftrightarrow\sqrt{1-x^2}=1\)
\(\Leftrightarrow1-x^2=1\)
\(\Leftrightarrow x=0\)
Đúng 1
Bình luận (0)
 giúp mình bài 4 câu B,C D với ạ
giúp mình bài 4 câu B,C D với ạ
Bài 4:
c) Ta có: \(\dfrac{x^3}{8}+\dfrac{x^2y}{2}+\dfrac{xy^2}{6}+\dfrac{y^3}{27}\)
\(=\left(\dfrac{x}{2}\right)^3+3\cdot\left(\dfrac{x}{2}\right)^2\cdot\dfrac{y}{3}+3\cdot\dfrac{x}{2}\cdot\left(\dfrac{y}{3}\right)^2+\left(\dfrac{y}{3}\right)^3\)
\(=\left(\dfrac{1}{2}x+\dfrac{1}{3}y\right)^3\)
\(=\left(\dfrac{-1}{2}\cdot8+\dfrac{1}{3}\cdot6\right)^3=\left(-4+2\right)^3=-8\)
Đúng 0
Bình luận (0)
Bài 6:
a) Ta có: \(P=\left(x+2\right)^3+\left(x-2\right)^3-2x\left(x^2+12\right)\)
\(=x^3+6x^2+12x+8+x^3-6x^2+12x-8-2x^3-12x\)
=0
b) Ta có: \(Q=\left(x-1\right)^3-\left(x+1\right)^3+6\left(x+1\right)\left(x-1\right)\)
\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1+6x^2-6\)
=-8
Đúng 0
Bình luận (0)
 giúp mình bài 2 câu c với d vs ạ
giúp mình bài 2 câu c với d vs ạ
Lời giải:
c.
$4(x+5)^3-7=101$
$4(x+5)^3=101+7=108$
$(x+5)^3=108:4=27=3^3$
$\Rightarrow x+5=3$
$\Rightarrow x=-2$
d.
$2^{x+1}.3+15=39$
$2^{x+1}.3=39-15=24$
$2^{x+1}=24:3=8=2^3$
$\Rightarrow x+1=3$
$\Rightarrow x=2$
Đúng 0
Bình luận (0)
ai giúp mình câu b,c,d bài 6 với ạ 
c: Gọi bốn số nguyên liên tiếp là x;x+1;x+2;x+3
Ta có: \(x\left(x+1\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+3x\right)\left(x^2+3x+2\right)+1\)
\(=\left(x^2+3x\right)^2+2\left(x^2+3x\right)+1\)
\(=\left(x^2+3x+1\right)^2\)
Đúng 0
Bình luận (0)
\(d,M=\left(x^2-4xy+4y^2\right)-2\left(x-2y\right)+1+9\\ M=\left(x-2y\right)^2-2\left(x-2y\right)+1+9\\ M=\left(x-2y+1\right)^2+9\ge9\\ M_{min}=9\Leftrightarrow x=2y-1\)
Đúng 1
Bình luận (0)
\(a,a^3+b^3+c^3=3abc\\ \Leftrightarrow a^3+b^3+c^3-3abc=0\\ \Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)=0\left(luôn.đúng.do.a+b+c=0\right)\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giúp mình giải câu b,c bài hình các bài tìm GTLN , GTNN với ạ mik đang cần gấp
a) \(A=\sqrt{1-x}+\sqrt{1+x}\)
\(\Rightarrow A^2=1-x+1+x+2\sqrt{\left(1-x\right)\left(1+x\right)}=2+2\sqrt{1-x^2}\)
Do \(-x^2\le0\Rightarrow1-x^2\le1\Rightarrow A^2=2+2\sqrt{1-x^2}\le2+2=4\)
\(\Rightarrow A\le2\)
\(maxA=2\Leftrightarrow x=0\)
Áp dụng bất đẳng thức: \(\sqrt{x}+\sqrt{y}\ge\sqrt{x+y}\)(với \(x,y\ge0\))
\(\Leftrightarrow\left(\sqrt{x}+\sqrt{y}\right)^2\ge x+y\)
\(\Leftrightarrow x+y+2\sqrt{xy}\ge x+y\Leftrightarrow2\sqrt{xy}\ge0\left(đúng\right)\)
\(A=\sqrt{1-x}+\sqrt{1+x}\ge\sqrt{1-x+1+x}=\sqrt{2}\)
\(maxA=\sqrt{2}\Leftrightarrow\)\(\left[{}\begin{matrix}1-x=0\\1+x=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Đúng 0
Bình luận (1)
b: Xét ΔABE vuông tại A có AH là đường cao ứng với cạnh huyền BE
nên \(BH\cdot BE=AB^2\left(1\right)\)
Xét ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC
nên \(AH\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BE=AH\cdot AC\)
Đúng 0
Bình luận (0)
Giúp mình câu c và d bài 4 tự luận với ạ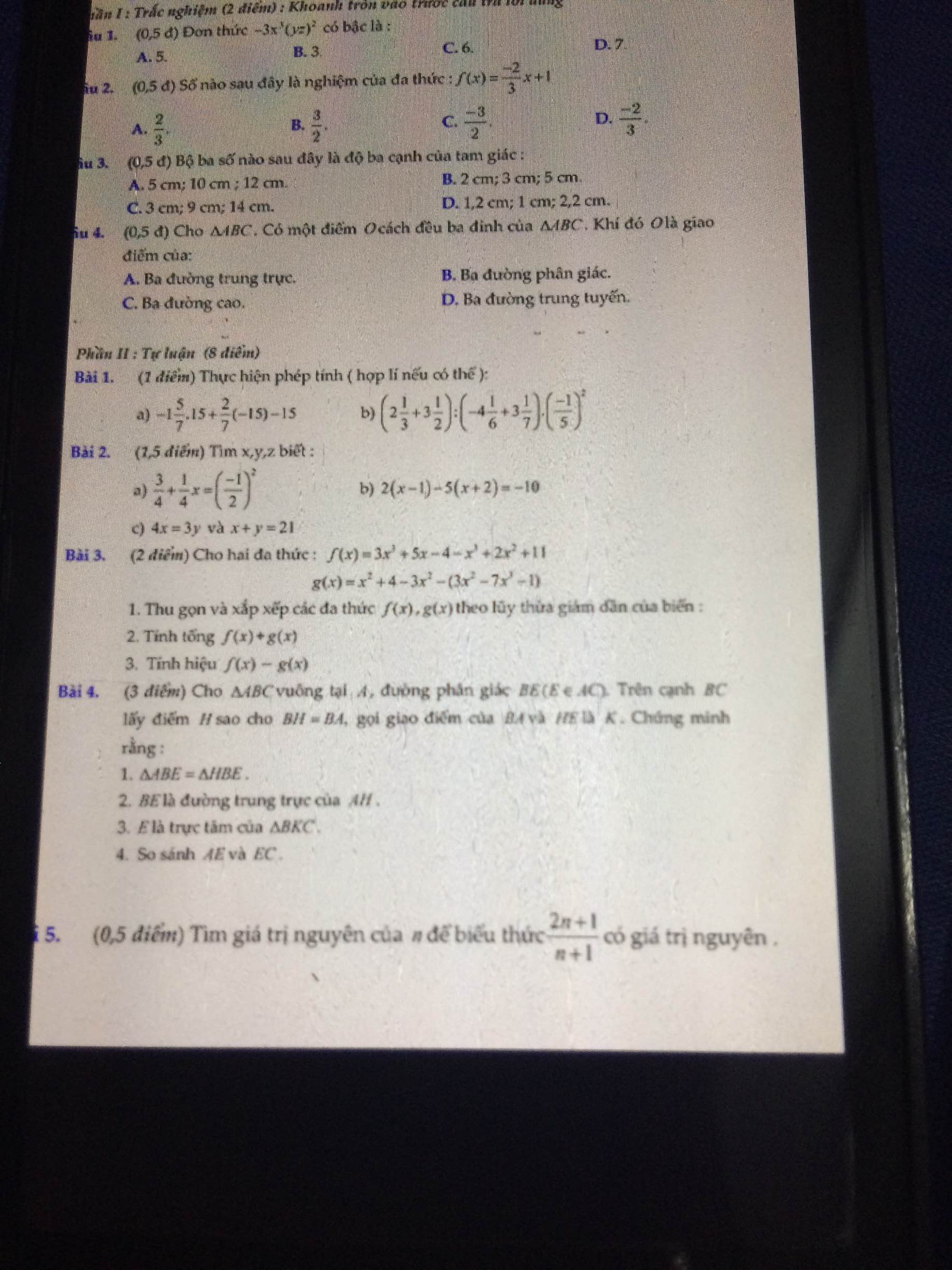
Bài 4:
a) Xét ΔABE và ΔHBE có
BA=BH(gt)
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
BE chung
Do đó: ΔABE=ΔHBE(c-g-c)
b) Ta có: ΔABE=ΔHBE(cmt)
nên EA=EH(hai cạnh tương ứng)
Ta có: BA=BH(gt)
nên B nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: EA=EH(cmt)
nên E nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BE là đường trung trực của AH
c) Ta có: ΔABE=ΔHBE(cmt)
nên \(\widehat{BAE}=\widehat{BHE}\)(hai góc tương ứng)
mà \(\widehat{BAE}=90^0\)(gt)
nên \(\widehat{BHE}=90^0\)
Xét ΔBKC có
KH là đường cao ứng với cạnh BC
CA là đường cao ứng với cạnh BK
KH cắt CA tại E
Do đó: E là trực tâm của ΔBKC(Tính chất ba đường cao của tam giác)
d) Ta có: EA=EH(cmt)
mà EH<EC(ΔEHC vuông tại H có EC là cạnh huyền)
nên EA<EC
Đúng 0
Bình luận (0)

Ai giúp mình phần 2 nhỏ bài tìm gtri nguyên n với câu 3 bài hình đc ko ạ(kèm vẽ hình) nếu cần thiết mn làm giúp e câu 5 ạ ko thì thôi ạ. Mình cảm ơn nhiều
Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)
Đúng 2
Bình luận (0)
Giúp mình bài 19 với câu d bài trên Với ạ😭
Bài 19:
a: \(A=5x+\dfrac{1}{9}y=5\cdot\dfrac{-1}{10}+\dfrac{1}{9}\cdot4.8=\dfrac{-1}{2}+\dfrac{8}{15}=\dfrac{-15+16}{30}=\dfrac{1}{30}\)
b: \(A=x-\dfrac{2}{3}=\dfrac{-1}{3}-\dfrac{2}{3}=-1\)
Đúng 1
Bình luận (0)
\(a,7x-2x-\dfrac{2}{3}y+\dfrac{7}{9}y=5x+\dfrac{1}{9}y\\ =5.\left(\dfrac{-1}{10}\right)+\dfrac{1}{9}.4,8\\ =\dfrac{-1}{2}+\dfrac{8}{15}=\dfrac{1}{30}\\ b,x=\dfrac{0,2-0,375+\dfrac{5}{11}}{-0,3+\dfrac{9}{16}-\dfrac{15}{22}}\\ =\dfrac{-1}{3}+\dfrac{\dfrac{-7}{40}+\dfrac{5}{11}}{\dfrac{21}{80}-\dfrac{15}{22}}\\ =\dfrac{-1}{3}+\dfrac{\dfrac{123}{440}}{\dfrac{-369}{880}}=\dfrac{-1}{3}+\dfrac{-2}{3}=\dfrac{-3}{3}=\left(-1\right)\)
Đúng 3
Bình luận (0)