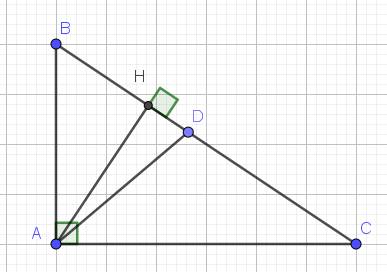
cho tam giác ABC,,BC= 10cm,góc b=30độ,c=40độ tính đường cao AH

Những câu hỏi liên quan
cho tam giác ABC,,BC= 10cm,góc b=30độ,c=40độ tính đường cao AH
kẻ đường cao AH ( H thuộc BC)
xét tam giác ABH có AH= BH .tanB
xét tam giác ACH có AH= CH.tanC
~> BH = CH.tanC/tanB
có BC = BH + CH = CH ( tanB + tanC)/tanB = 9
CH=9tanB/(tanB+tanC)
xét tam giác ACH có AC=CH/cosC
~> AC =7,91
Đúng 0
Bình luận (0)
cho tam giác ABC,,BC= 10cm,góc b=30độ,c=40độ tính đường cao AH giúp mình
cho tam giac ABC (AB=AC),kẻ đường cao AH (H ∈ BC)
a.c/m HB=HC và goc BAH=goc CAH
b.từ H kẻ HD vuông góc AB(D ∈ AB), kẻ HE vuong góc AC(E ϵ AC).C/m rằng AD=AE và tam giác HDE là tam giác cân
c.giả sử AB=10cm, BH=6cm. Hãy tính độ dài AH
ai giup vs![]()
a, xét tam giác HAB và tam giác HAC ta có
AB=AC(gt)
góc BAH= góc AHC ( 2 góc tương ứng )
AH ( chung)
=>tam giác AHD = Tam giác AHC ( c. g.c)
=> HB=HC ( hai cạnh tương ứng )
=>góc AHC=góc AHD ( hai góc tương ứng)
b,xét tam giác ADH và tam giác AEH ta có
AH ( chung )
góc ADH = góc AEH ( ..)
c. Tam giac ABC vuông tại C
2 2 2
=> BC =AB +AC
2 2 2
=>10 = 9 + AC
2
=>AC = 100-81 =19
=>AC = 4.35
Đúng 0
Bình luận (2)
cho tam giác ABC có góc B= 450, góc C= 300, cạnh BC= 10cm và đg cao AH. tính BH,CH,AH
cho tam giác ABC vuông tại A có AB=3cm,AC=4cm đường AH .a,Tính BC,AH ,b tính góc B ,góc C,c, phân giác của góc A cắt BC tại E .Tình BE,CE
a) Áp dụng ĐL Pytago vào tam giác ABC: BC^2= AB^2+AC^2= 3^2+4^2=25 =>> BC=5
Áp dụng hệ thức lượng: AH.BC=AB.AC => AH.5=3.4 => AH= 2,4
b) Áp dụng tỉ số lượng giác: sinB= AC/BC= 4/5= 0,8 => góc B= 59 độ
Góc C= 180-90-59= 31 độ
c) Áp dụng Pytago vào tam giác BHA: BH=1,8 (tự tính)
Góc BAH= 180-90-59= 31 độ
Góc BAE= 90/2= 45 độ (phân giác)
Góc HAE= 45 - 31= 14 độ
HE= tanHAE. AH= tan14. 2,4= 0,53
BE= HE+ BH= 0,53 + 1,8 = 2,33
CE= BC - BE= 5-2,33= 2,67
MẤY BÀI NÀY CHỈ CẦN THUỘC CÔNG THỨC LÀ LÀM ĐƯỢC HẾT .-. CHỊU KHÓ HỌC THUỘC ĐI RỒI MẤY BÀI NÀY SẼ TRỞ NÊN ĐƠN GIẢN ĐẾN BẤT NGỜ :))) ĐÂY LÀ KIẾN THỨC CŨ KO BIẾT LÀM ĐÚNG KO NỮA :33 HÊN XUI NHÁ!!
CỐ LÊN BABEEE <3
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A và AB =12cm, AC =16cm .Đường phân giác góc A cắt BC tại D
a) Tính BC ,BD vad CD ĐS: BC =20cm , BD≈8,6cm ,DC≈11,4 cm
b) Vẽ đường cao AH .Tính AH ,HD và AD ĐS: AH ≈9.6 cm , HD ≈1,4cm , AD ≈9,7 cm
Lời giải:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20$ (cm)
Áp dụng tính chất đường phân giác:
$\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}$
Mà: $BD+DC=BC=20$ nên:
$BD=20:(3+4).3=\frac{60}{7}$ (cm)
$CD= 20:(3+4).4=\frac{80}{7}$ (cm)
b.
$AH=2S_{ABC}:BC=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-9,6^2}=7,2$ (cm)
$HD = BD-BH = \frac{60}{7}-7,2=\frac{48}{35}$ (cm)
$AD = \sqrt{AH^2+HD^2}=\sqrt{9,6^2+(\frac{48}{35})^2}=\frac{48\sqrt{2}}{7}$ (cm)
Đúng 2
Bình luận (0)
a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=12^2+16^2=20^2\)
=>\(BC=20\left(cm\right)\)
Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
=>\(\dfrac{BD}{12}=\dfrac{CD}{16}\)
=>\(\dfrac{BD}{3}=\dfrac{CD}{4}\)
mà BD+CD=BC=20
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{20}{7}\)
=>\(BD=\dfrac{20}{7}\cdot3=\dfrac{60}{7}\left(cm\right);CD=\dfrac{20}{7}\cdot4=\dfrac{80}{7}\left(cm\right)\)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot20=12\cdot16=192\)
=>\(AH=\dfrac{192}{20}=9,6\left(cm\right)\)
Ta có: ΔAHB vuông tại H
=>\(HB^2+AH^2=AB^2\)
=>\(HB^2=12^2-9,6^2=51,84\)
=>\(HB=\sqrt{51,84}=7,2\left(cm\right)\)
=>HC=BC-HB=12,8(cm)
Vì CD<CH
nên D nằm giữa C và H
=>CD+DH=CH
=>\(DH=12.8-\dfrac{80}{7}=\dfrac{48}{35}\left(cm\right)\)
ΔAHD vuông tại H
=>\(AH^2+HD^2=AD^2\)
=>\(AD^2=\left(\dfrac{48}{35}\right)^2+9,6^2=\dfrac{4608}{49}\)
=>\(AD=\sqrt{\dfrac{4608}{49}}=\dfrac{48\sqrt{2}}{7}\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC , có AC=16, AB=12,BC=20
a) c/m:tam giác ABC vuông
b) kẻ đường cao AH. tính AH, góc BAH, góc CAH.
c) kẻ HE vuông AC tại E, HF vuông AB tại F. Tính HE, HF.
d)C/m: AB.AF=AE.AC
Cho tam giác ABC vuông tại A, AB= 4.5 cm, AC=6cm. Kẻ đường cao AH đường trung tuyến AD ( H và D thuộc BC)
a) C/M: tam giác HBA đồng dạng với tam giác ABC
b) Tính độ dài AH và diện tích tam giác AHB.
c) Kẻ các đường phân giác DE cùa góc ADB và DF của góc ADC ( E thuộc AB, F thuộc AC)
C/M: EF song song với BC
a) xét tam giác ABC và tam giác HBA có:
BAC=BHA (90°)
B chung
=> tam giác ABC~ tam giác HBA (g.g)
b) Áp dụng định lý py ta go trong tam giác ABC vuông tại A
BC 2 = AC 2 + AB 2
BC 2 = (4,5)2 + (6)2
BC 2 = 20.25 + 36
BC 2 = 56.25
BC = căn 56.25 = 7.5 (cm)
c) Áp dụng định lý đảo ta lét ta có
AE/ AB = AF / AC (E € AB, F € AC)
=> EF// BC
Đúng 0
Bình luận (0)
Cho tam giác ABC có số đo góc BAC bằng 90 độ.Kẻ đường cao AH của tam giác ABC ( H thuộc BC) và tia phân giác AM của góc BAH ( M thuộc BC )
a) chứng minh rằng góc ABC và HAC bằng nhau
b) cho số đo các góc MAC = 70 độ. Tính góc AMC?