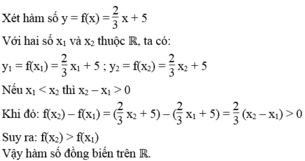Cho hàm số y=-2x + 5. Chứng minh rằng hàm số nghịch biến trên R

Những câu hỏi liên quan
1
cho hàm số y=f (x)=-2x chứng minh hàm số nghịch biến trên tập số thực R
Gọi x1, x2 là hai giá trị của x (x1>x2)
Ta có: x1>x2\(\Leftrightarrow\)-2x1<-2x2 \(\Leftrightarrow\)f(x1) < f(x2)
Vì x1>x2 mà f(x1) < f(x2) suy ra hàm số nghịch biến trên tập hợp số thực R
Đúng 2
Bình luận (0)
Vì a=-2
nên hàm số y=-2x nghịch biến trên R
Đúng 0
Bình luận (0)
Cho hàm số y = f(x) = 4 - 2/5x với x ∈ R. Chứng minh rằng hàm số đã cho nghịch biến trên R.
Với x 1 , x 2 là hai giá trị bất kì của x thuộc R, ta có:
y 1 = f( x 1 ) = 4 - 2/5 x 1 ; y 2 = f( x 2 ) = 4 - 2/5 x 2
Nếu x 1 < x 2 thì x 1 - x 2 < 0. Khi đó ta có:
y 1 - y 2 = (4 - 2/5 x 1 ) - (4 - 2/5 x 2 )
= (-2)/5( x 1 - x 2 ) > 0. Suy ra y 1 > y 2
Vậy hàm số đã cho là hàm nghịch biến trên R.
Đúng 0
Bình luận (0)
Chứng minh rằng hàm số y = 2 x - x 2 đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).
TXĐ: D = [0; 2]
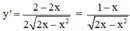
+ Hàm số đồng biến
⇔ y’ > 0
⇔ 0 < x < 1.
+ Hàm số nghịch biến
⇔ y’ < 0
⇔ 1 < x < 2.
Vậy hàm số đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).
Đúng 0
Bình luận (0)
Cho hàm số y=-5/9x-6
a) Tính f(-1),f(0),f(2),f(1/2)
b)Chứng minh hàm số luôn nghịch biến trên R
b: Vì \(a=-\dfrac{5}{9}< 0\) nên hàm số luôn nghịch biến trên R
Đúng 1
Bình luận (0)
Cho hàm số y = f(x) = 2 3 x + 5 với x ∈ R. Chứng minh rằng hàm số đồng biến trên R.
Vẽ đồ thị của các hàm số \(y=3x+1\) và \(y=-2x^2\). Hãy cho biết:
a) Hàm số \(y=3x+1\) đồng biến hay nghịch biến trên R.
b) Hàm số \(y=-2x^2\) đồng biến hay nghịch biến trên mỗi khoảng: \(\left(-\infty;0\right)\) và \(\left(0;+\infty\right)\)
Vẽ đồ thị \(y = 3x + 1;y = - 2{x^2}\)

a) Trên \(\mathbb{R}\), đồ thị \(y = 3x + 1\) đi lên từ trái sang phải, như vậy hàm số \(y = 3x + 1\) đồng biến trên \(\mathbb{R}\)
b) Trên khoảng \(\left( { - \infty ;0} \right)\), đồ thị \(y = - 2{x^2}\)đi lên từ trái sang phải với mọi \(x \in \left( { - \infty ;0} \right)\) , như vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị \(y = - 2{x^2}\)đi xuống từ trái sang phải với mọi \(x \in \left( {0; + \infty } \right)\) , như vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)
Đúng 0
Bình luận (0)
Cho hàm số \(y=f\left(x\right)=4-\dfrac{2}{5}x\) với \(x\in\mathbb{R}\)
Chứng minh rằng hàm số đã cho nghịch biến trên \(\mathbb{R}\)
Cho hàm số y=2x-1
Hàm số trên đồng biến hay nghịch biến trên R vì sao
Cho hàm số bậc nhất y=-2x+5
a, hàm số đã cho đồng biến hay nghịch biến R? Vì sao?
b, vẽ đồ thị hàm số trên
a: Hàm số này nghịch biến vì -2<0
Đúng 0
Bình luận (0)