Tam giác ABC vuống tại A có AB bằng 3cm AC bằng 4cm. Tính bán kính đường nội tiếp tam giác.

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại D và E. Tính bán kính của đường tròn (O) biết AB = 3cm, AC = 4cm.
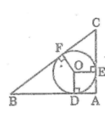
Áp dụng định lí Pitago vào tam giác vuông ABC ta có :
B C 2 = A B 2 + A C 2 = 3 2 + 4 2 = 25
Suy ra : BC = 5 (cm)
Theo tính chất hai tiếp tuyến giao nhau ta có:
AD = AE
BD = BF
CE = CF
Mà: AD = AB – BD
AE = AC – CF
Suy ra: AD + AE = AB – BD + (AC – CF)
= AB + AC – (BD + CF)
= AB + AC – (BF + CF)
= AB + AC – BC
Suy ra:
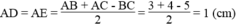
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB,AC lần lượt tại D,E
a)ADOE là hình gì? Vì sao?
b)Tính bán kính của (O) biết AB=3cm, AC=4cm
Cho tam giác ABC vuông tại A. Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại D, E
a) Tứ giác ADOE là hình gì ? Vì sao ?
b) Tính bán kính của đường tròn (O) biết AB = 3cm, AC = 4cm ?
a) tứ giác ADOE là hình vuông
vì \(\left\{{}\begin{matrix}DAE=90\left(giảthiết\right)\\ODA=90\left(DlàtiếpđiểmcủađườngtrònvớiAB\right)\\OEA=90\left(Elàtiếpđiểmcủađườngtròn\:vớiAC\right)\end{matrix}\right.\)
và OD = OE = R
Đúng 0
Bình luận (0)
Tính các cạnh của một tam giác ABC có bán kính đường tròn nội tiếp bằng 3cm, tiếp điểm trên cạnh AB chia cạnh ấy thành 2 đoạn thẳng AF = 3cm, FB = 4cm
Cho tam giác ABC có góc A bằng 60 độ , AB=2cm, AC= 4cm.
a) Tím diện tích tam giác ABC
b) Tính BC
c) Gọi r là bán kính đường tròn nội tiếp tam giác ABC . Tính r
1. Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R = 3cm. Tính diện tích hình quạt tạo bởi hai bán kính OB,OC và cung nhỏ BC khi \(\widehat{BAC}=60^o\)
2. Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm nội tiếp đường tròn (O). Tính diện tích hình tròn (O)
2: ΔABC vuông tại A nội tiếp (O)
=>O là trung điểm của BC
BC=căn 6^2+8^2=10cm
=>OB=OC=10/2=5cm
S=5^2*3,14=78,5cm2
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A nội tiếp đường tâm O, biết AB = 3cm, AC = 4cm. a) tính bán kính của (O) . b) vẽ đường kính AD. Chứng minh : ABCD là hình chữ nhật. c) kẻ AH vuông góc với BC tại H. Chứng minh: AB. AC = AH. AD
a: \(R=\dfrac{BC}{2}=2.5\left(cm\right)\)
b: Xét tứ giác ABDC có
O là trung điểm của AD
O là trung điểm của BC
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB 4cm, AC3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D
Cho tam giác ABC vuông tại A có AB4cm, AC3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D.
a) Tính độ dài đoạn thẳng AH
b) Chứng minh BD là tiếp tuyến của đường tròn (C)
c) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA,BD thứ tự E,F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua...
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = 4cm, AC=3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D Cho tam giác ABC vuông tại A có AB=4cm, AC=3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D. a) Tính độ dài đoạn thẳng AH b) Chứng minh BD là tiếp tuyến của đường tròn (C) c) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA,BD thứ tự E,F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua M kẻ tiếp tuyến với (C) cắt AB,BD lần lượt tại P,Q. Chứng minh EF bình phương =4PE.QF
a:\(BC=\sqrt{4^2+3^2}=5\left(cm\right)\)
AH=4*3/5=2,4cm
b: ΔCAD cân tại C
mà CH là đường cao
nên CH là phân giác của góc ACD
Xét ΔCAB và ΔCDB có
CA=CD
góc ACB=góc DCB
CB chung
Do dó: ΔCAB=ΔCDB
=>góc CDB=90 độ
=>BD là tiếp tuyến của (C)
Đúng 0
Bình luận (0)
cho tam giác abc có góc a bằng 90 độ. hai đường phân giác các góc B và C cắt nhau tại biết I. AB=5 AC=12. Tính độ dài bán kính đường tròn nội tiếp tam giác ABC
Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2\)=\(AB^2+AC^2\)
⇔\(BC^2\)= 52 + 122 =169
hay BC = 13cm
Ta có: ΔABC vuông tại A
nên bán kính đường tròn ngoại tiếp ΔABC là một nửa của cạnh huyền BC
hay
Đúng 0
Bình luận (0)



















