Giải giúp mình với giải hết chi tiết ak

Những câu hỏi liên quan
55470 :86
Giải chi tiết giúp mình ak
Cảm ơn các bn NHÌU
- -
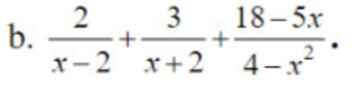 Giải giúp mình với,chi tiết hết luôn ạ,xin cảm ơn
Giải giúp mình với,chi tiết hết luôn ạ,xin cảm ơn
ĐKXĐ: \(x\ne\pm2\)
\(\dfrac{2}{x-2}+\dfrac{3}{x+2}+\dfrac{18-5x}{4-x^2}=\dfrac{2\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{5x-18}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x+4+3x-6+5x-18}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{10x-20}{\left(x-2\right)\left(x+2\right)}=\dfrac{10\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{10}{x+2}\)
Đúng 1
Bình luận (0)
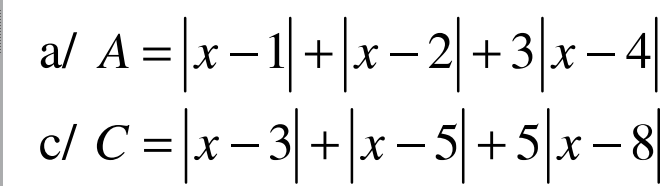
Tính GTNN
Mình cần rất rất gấp lời giải chi tiết 2 phần này. . Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn
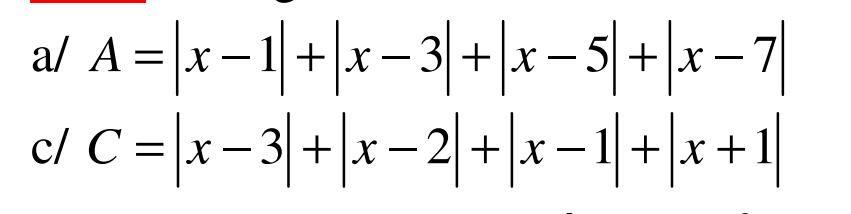
Tính GTNN
Mình cần rất rất gấp lời giải chi tiết 2 phần này. . Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn
https://hoc24.vn/cau-hoi/minh-can-rat-rat-gap-loi-giai-chi-tiet-2-phan-nay-de-bai-la-tinh-gtnn-moi-ng-giup-minh-voiiiiiiiiiiiiiiiiiiiii-ak-minh-cam-on.1527826665808
Mình làm ở đây rồi bạn nhé. Bạn vào link này tham khảo.
Đúng 0
Bình luận (0)
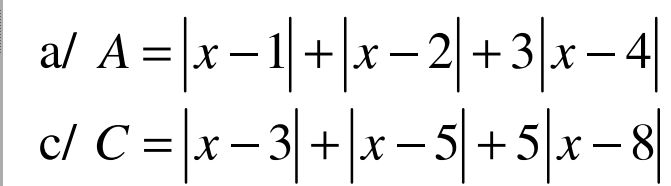
Tìm GTNN
Mình cần rất rất gấp lời giải chi tiết 2 phần này. Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn
a. Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$|x-1|+|x-4|=|x-1|+|4-x|\geq |x-1+4-x|=3$
$|x-2|+|x-4|=|x-2|+|4-x|\geq |x-2+4-x|=2$
$|x-4|\geq 0$
Cộng theo vế:
$A\geq 5$
Vậy $A_{\min}=5$. Giá trị này đạt tại \(\left\{\begin{matrix} (x-1)(4-x)\geq 0\\ (x-2)(4-x)\geq 0\\ x-4=0\end{matrix}\right.\Leftrightarrow x=4\)
Đúng 1
Bình luận (0)
c. Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ thì:
$|x-3|+|x-8|=|x-3|+|8-x|\geq |x-3+8-x|=5$
$|x-5|+|x-8|=|x-5|+|8-x|\geq |x-5+8-x|=3$
$3|x-8|\geq 0$
Cộng theo vế:
$C\geq 8$. Vậy $C_{\min}=8$. Giá trị này đạt tại $x=8$
Đúng 1
Bình luận (0)
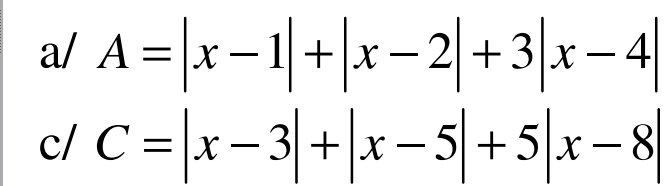
Tính GTNN
Mình cần rất rất gấp lời giải chi tiết 2 phần này. . Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn
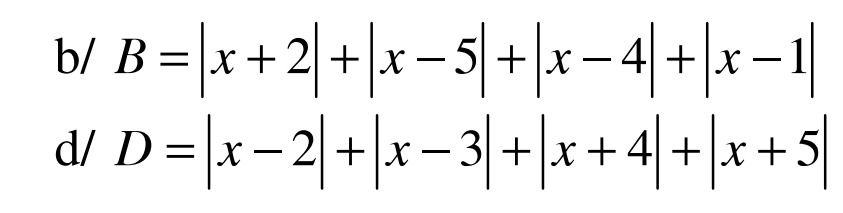
Mình cần rất rất gấp lời giải chi tiết 2 phần này. đề bài là tính GTNN. Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn
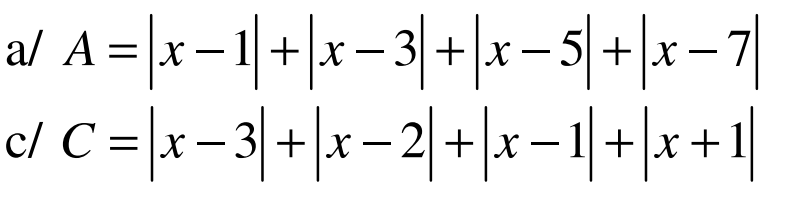
Mình cần rất rất gấp lời giải chi tiết 2 phần này. đề bài là tính GTNN. Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn
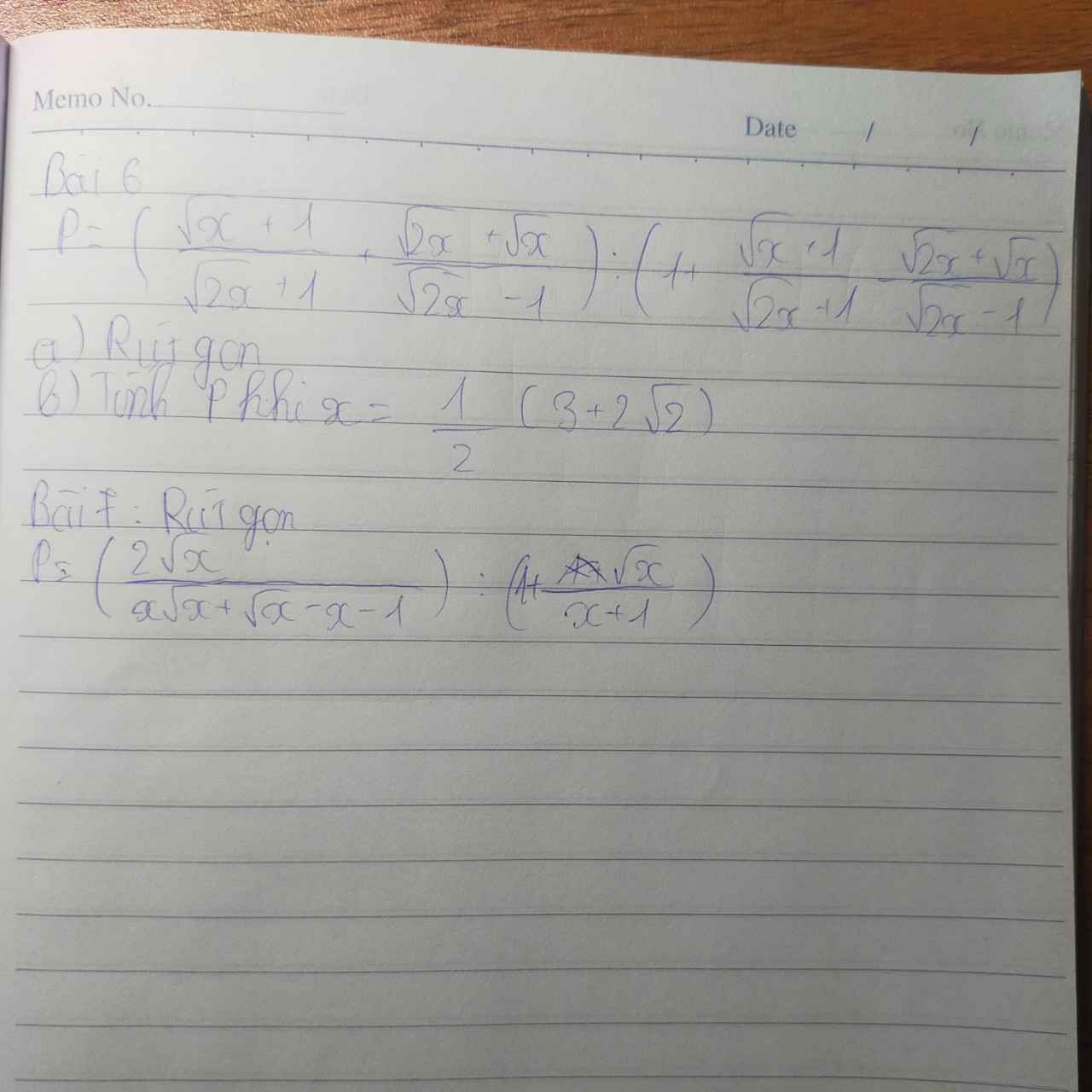
Giải chi tiết giúp em với ạ
Cảm ơn mn
#hứa vote ctrl hay nhất ak <3
Bài 7:
Ta có: \(P=\left(\dfrac{2\sqrt{x}}{x\sqrt{x}+\sqrt{x}-x-1}\right):\left(1+\dfrac{\sqrt{x}}{x+1}\right)\)
\(=\dfrac{2\sqrt{x}}{\left(x+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{x+1}{x+\sqrt{x}+1}\)
\(=\dfrac{2\sqrt{x}}{x\sqrt{x}-1}\)
Đúng 0
Bình luận (0)
















