GIÚP MÌNH VỚI NHA!!! LÀM ƠN!
Cho hình thoi ABCD có góc A = 60o. Hãy tính tỉ số \(\frac{AC^2}{AB^2}\)
Những câu hỏi liên quan
Cho hình thoi ABCD có diện tích bằng 50√3cm^2 và AC=10cm
1/ Tính độ dài BD và AB
2/ Tính số đo các góc của hình thoi ABCD
Giúp em câu 2 với ạ, em cảm ơn.
1) \(S_{ABCD}=\dfrac{1}{2}.AC.BD\Rightarrow BD=\dfrac{2S_{ABCD}}{AC}=\dfrac{2.50\sqrt[]{3}}{10}=10\sqrt[]{3}\left(cm\right)\)
Gọi O là giao điểm AC và BD
\(\Rightarrow\left\{{}\begin{matrix}OA=\dfrac{1}{2}AC=5\left(cm\right)\\OB=\dfrac{1}{2}BD=5\sqrt[]{3}\left(cm\right)\end{matrix}\right.\)
Xét Δ vuông OAB có :
\(AB^2=OA^2+OC^2=25+25.3=100\left(cm^2\right)\left(Pitago\right)\)
\(\Rightarrow AB=10\left(cm\right)\)
2) Xét Δ vuông OAB có :
\(AB=2OA=10\left(cm\right)\)
⇒ Δ OAB là Δ nửa đều
\(\Rightarrow\left\{{}\begin{matrix}\widehat{ABD}=30^o\\\widehat{BAC}=60^o\end{matrix}\right.\)
mà \(\left\{{}\begin{matrix}\widehat{BCD}=\widehat{BAD}=2\widehat{BAC}\\\widehat{ADC}=\widehat{ABC}=2\widehat{ABD}\end{matrix}\right.\) (tính chất hình thoi)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{BCD}=\widehat{BAD}=2.60=120^o\\\widehat{ADC}=\widehat{ABC}=2.30=60^o\end{matrix}\right.\)
Đúng 3
Bình luận (0)
6 tháng 3 2022 lúc 9:24
Vẽ hình giúp mik và làm giúp mình với:
Bài 2:
Cho △ABC ⊥ tại A, có góc B = 60o và AB = 5 cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC tại E
a) C/m △ABC = △EBD
b) C/m △ABE là △đều
c) Tính độ dài AC
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên BA=BE
=>ΔBAE cân tại B
mà \(\widehat{ABE}=60^0\)
nên ΔBAE đều
c: Xét ΔABC vuông tại A có
\(\tan B=\dfrac{AC}{AB}\)
\(\Leftrightarrow AC=5\sqrt{3}\left(cm\right)\)
Đúng 1
Bình luận (0)
Hình thoi ABCD có góc A bằng 60o đường thẳng MN cắt cạnh AB,AC theo thứ tự M,N Biết MB+NB bằng độ dài cạnh hình thoi Tính góc MDN
Cho hình thoi ABCD có A=60 tính tỉ số \(\frac{AC^2}{AB^2}\)
cho tam giác ABC vuông tại A có góc BAC=60, kẻ tia Ax song song với BC. Trên Axlấy điểm D sao cho AD=DC
a)Tíng góc BAD và góc DAC
b)Chứng minh tứ giác ABCD là hình thang cân
c)Gọi E là trung điểm của BC . Chứng minh tứ giác ADEB là hình thoi
d)Cho AC=8cm, AB=5cm. Tính diện tích hình thoi ABED
các bạn làm giúp mik nha cảm ơn nhiều mik đang cần gấp.Vẽ cả hình nữa nha
mik ko bt dc thấy cô giáo giao de nhu the
Đúng 0
Bình luận (0)
Vẽ hình rồi giải
Cho hình thang cân ABCD ( AB//CD) và AB=2CD , AB= AD+CB
a) Tính các góc của hình thang
b) Tính góc hợp bởi 2 đường chéo
c) CM AC vuông góc với CB
Nếu các bạn có thể làm hết thì hãy làm hết giúp mik , mik cảm ơn
Cho hình lăng trụ ABCD.ABCD có hình chiếu A lên mp(ABCD) là trung điểm AB, ABCD là hình thoi cạnh 2a, góc
A
B
C
^
60
O
,BB tạo với đáy một góc
30
o
. Tính thể tích hình lăng trụ ABCD.ABCD A.
a...
Đọc tiếp
Cho hình lăng trụ ABCD.A'B'C'D' có hình chiếu A' lên mp(ABCD) là trung điểm AB, ABCD là hình thoi cạnh 2a, góc A B C ^ = 60 O ,BB' tạo với đáy một góc 30 o . Tính thể tích hình lăng trụ ABCD.A'B'C'D'
A. a 3 3
B. 2 a 3 3
C. 2 a 3
D. a 3
Đáp án là C
Gọi H là hình chiếu của A’ trên (ABCD). Dễ thấy góc
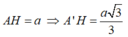
Dễ dàng tính được diện tích đáy
Đúng 0
Bình luận (0)
Cho hinh thang vuông ABCD có AB = 20cm AD = 30cm DC = 40cm Nối A với C được hai hình tam giác là ABC và ADC. Tính
A) diện tích của mỗi hình tam giác
B) Tỉ số phần trăm của diện tích tam giác ABC và diện tích tam giác ADC
Thông cảm ko bik vẽ hình nên bik chi thoi giúp mình nha làm ơn
ABC =300 cm
ADC=600 cm
thông cảm cho mình nha ko biết gõ kí hiệu vuông
Đúng 0
Bình luận (0)
Minh khong biet
Mình mới học lớp 4
Đáp số:Minh moi hoc lop 4
Đúng 0
Bình luận (0)
Các bạn giúp mình giải gấp mấy bài này với ạ, làm ơn ghi rõ ràng kĩ càng lời giải với nhé *nếu tiện thì phiền vẽ hình giùm mình luôn*. Mơn nhiều nha ^^a) HÌnh thanh ABCD ( AB // CD ) có góc A - góc D 20 độ ; góc B 2 lần gócC . Tính các góc của hình thangb) Cho tam giác ABC cân tại A, các đường phân giác BD,CE ( D thuộc AC, E thuộc AB ) . Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bênc) Hình thang ABCD ( AB//CD ) có góc ACD góc BDC . Chứng minh rằng ABCD là hình thang cân
Đọc tiếp
Các bạn giúp mình giải gấp mấy bài này với ạ, làm ơn ghi rõ ràng kĩ càng lời giải với nhé *nếu tiện thì phiền vẽ hình giùm mình luôn*. Mơn nhiều nha ^^
a) HÌnh thanh ABCD ( AB // CD ) có góc A - góc D = 20 độ ; góc B = 2 lần gócC . Tính các góc của hình thang
b) Cho tam giác ABC cân tại A, các đường phân giác BD,CE ( D thuộc AC, E thuộc AB ) . Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên
c) Hình thang ABCD ( AB//CD ) có góc ACD = góc BDC . Chứng minh rằng ABCD là hình thang cân
c,
- Gọi O là giao điểm của AC và BD.
- AB//CD nên góc BAC = góc ACD (so le trong), tương tự góc ABD=góc BDC.
- Theo đề bài góc ACD=gócBDC nên góc BAC=góc ABD.
=>Tam giác ABO cân tại O => 0A=0B.(1)
Tương tự tam giác ODC cân tại O =>OD=OC.(2)
Lại có góc AOD=góc BOC (đối đỉnh ) (3)
Từ (1), (2), (3) suy ra tam giác AOD = tam giác OBC nên suy ra :
+ AD=BC (*)
+ Góc ADB=góc BCA(**)
Từ (*) và (**) suy ra hình thang ABCD cân(hình thang có hai cạnh bên bằng nhau và hai góc ở đáy bằng nhau )
Đúng 0
Bình luận (0)