Một ca nô xuôi dòng từ A đến B rồi quay trở về A với vận tốc thực là 14km/h.Vận tốc dòng nước 2km/h.Biết thời gian ca nô xuôi dòng ít hơn thời gian ngược dòng là 1h.Tình quãng đường AB "_"

Những câu hỏi liên quan
Một cano xuôi dòng từ A đến B rồi quay trở về A với vận tốc thực là 14 km/h.Vận tốc dòng nước là 2 km/h.Biết thời gian cano xuôi dòng ít hơn thời gian cano ngược dòng là 1 giờ.Tính quãng đường AB
Một ca nô chạy xuôi dòng sông một quãng đường 9km, sau đó quay ngược trở lại đến một địa điểm cách nơi xuất phát 1km thì dừng lại. Biết thời gian đi xuôi dòng ít hơn thời gian ngược dòng là 15 phút và vận tốc của dòng nước là 2km/h. Tính vận tốc của ca nô khi nước đứng yên?
15 phút = (1/4)giờ
Gọi vận tốc của ca nô khi nước đứng yên là x (km/h). Điều kiện x > 2
Vận tốc ca nô khi xuôi dòng là x + 2 (km/h)
Vận tốc ca nô khi ngược dòng là x – 2 (km/h)
Thời gian ca nô khi xuôi dòng là:
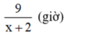
Thời gian ca nô khi ngược dòng là:
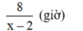
Ta có phương trình:
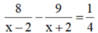
Quy đồng mẫu hai vế:
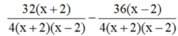
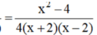
Suy ra:
32x + 64 - 36x + 72 = x2 - 4
⇔ -4x + 136 = x2 - 4
⇔ x2 + 4x - 140 = 0
⇔ (x2 + 4x + 4) - 144 = 0
⇔ (x + 2)2 - 122 = 0
⇔ (x + 14)(x - 10) = 0
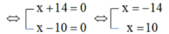
Giá trị x = -14 không thỏa mãn điều kiện
Giá trị x = 10 thỏa mãn điều kiện
Vậy vận tốc của ca nô khi nước yên lặng là 10km/h
Đúng 1
Bình luận (0)
Một ca nô xuôi dòng từ A đến B và ngược dòng từ B về A. Biết quãng đường AB dài 60km và thời gian ngược dòng nhiều hơn thời gian xuôi dòng 1 giờ. Tính vận tốc thực của ca nô, biết vận tốc dòng nước là 1km/h
Xem chi tiết
Gọi vận tốc thực của cano là x(km/h) (x>1)
Vận tốc xuôi dòng: x+1 (km/h)
Vận tốc ngược dòng x - 1(km/h)
Thời gian xuôi dòng: \(\dfrac{60}{x+1}\)(h)
Thời gian ngược dòng : \(\dfrac{60}{x-1}\left(h\right)\)
Theo bài ta có :
\(\dfrac{60}{x-1}-\dfrac{60}{x+1}=1\)
=> \(\dfrac{60\left(x+1\right)}{x^2-1}-\dfrac{60\left(x-1\right)}{x^2-1}=\dfrac{x^2-1}{x^2-1}\)
=> 60x + 60 - 60x + 60 = x2 - 1
=> 120 = x2 - 1
=> x2 = 121 => x = 11 (tm)
Vậy vận tốc thực cano là 11km/h
Đúng 2
Bình luận (0)
Một ca nô xuôi dòng từ A đến B rồi lại từ B về A với vận tốc thực là 27km/h. Tính AB, biết vận tốc của dòng nước là 3km/h, thời gian ca nô đi ngược dòng nhiều hơn thời gian ca nô đi xuôi dòng là 20 phút
Đổi 20 phút = 1/3 h
Gọi x (km) là độ dài quãng đường AB (x > 0)
Thời gian khi đi xuôi dòng: x/30 (h)
Thời gian khi đi ngược dòng: x/24 (h)
Theo đề bài ta có phương trình:
x/24 - x/30 = 1/3
⇔ 5x - 4x = 40
⇔ x = 40 (nhận)
Vậy quãng đường AB dài 40 km
Đúng 1
Bình luận (0)
Một chiếc ca nô xuôi dòng sông một đoạn 9km và quay trở về đi ngược dòng sông, đến một địa điểm cách chỗ xuất phát ban đầu 1km thì dừng lại. Vận tốc của dòng nước là 2km/h . Thời gian đi xuôi dòng ít hơn thời gian đi ngược dòng là 15 phút . Tính vận tốc thực của ca nô .
Gọi vận tốc thực của ca nô là: x (km/giờ) (ĐK: x > 0)
Thời gian đi xuôi dòng là: 9/(2 + x) (giờ)
Thời gian đi ngược dòng là: 8/(2 - x) (giờ)
=> Ta có PT:
\(\frac{8}{\left(2-x\right)}-\frac{9}{\left(2+x\right)}=\frac{1}{4}\)
\(\Leftrightarrow\orbr{\begin{cases}x=10\left(\text{TM}\right)\\x=-14\left(\text{loai}\right)\end{cases}}\)
Đúng 0
Bình luận (1)
Ta có: 15 phút =\(\frac{1}{4}\)giờ
Gọi vân tốc cano khi nước đứng yên là x,x>0 và tính bằng km/h
Đến đây, có 4 đại lượng biểu diễn là:
-Vận tốc cano xuôi dòng
-Vận tốc cano đi ngược dòng
-Thời gian cano đi xuôi dòng
-Thời gian cano đi ngược dòng
Các đại lượng này được thể hiện trong bảng sau
| Xuôi dòng | Ngược dòng | Chênh lệch | |
| Vận tốc | x+2 | x-2 | |
| Thời gian | \(\frac{9}{x+2}\) | \(\frac{8}{x-2}\) | \(\frac{8}{x-2}-\frac{9}{x+2}\) |
Nhìn vào bảng, ta dễ dàng lập phương trình:
\(\frac{8}{x-2}-\frac{9}{x+2}=\frac{1}{4}\)ĐK: \(x\ne\pm2\)
Mẫu chung là: 4(x-2)(x+2)
Quy đồng và khử mẫu, ta đưa về phương trình
x2+4x-140=0
<=> (x-10)(x+14)=0
<=> x1=10; x2=-14
Giá trị x2=-14 (loại) vì x>0
Vậy vận tốc thực của cano là 10km/h
*Trình bày bài bạn không cần đưa bảng vào nhé*
Bài 1: khoảng cách giữa 2 bến sông A và B là 30km. Một ca nô đi xuôi dòng từ bến A đến bến B rồi lại ngược dòng từ B về A. Thời gian ca nô xuôi dòng ít hơn thời gian ca nô ngược dòng là 1h. Tìm vận tốc của ca nô khi nước yên lặng, biết vận tốc dòng nước là 4km/h Bài 2: Hai bến sông cách nhau 15km. Thời gian ca nô xuôi dòng từ bến A đến Bến B, tại bến B nghỉ 20 rồi ngược dòng từ bến B trở lại bến A tổng cộng là 3h. Tính vận tốc của ca nô khi nước yên lặng, biết vận tốc dòng nước là 3km/h Bài 3: M...
Đọc tiếp
Bài 1: khoảng cách giữa 2 bến sông A và B là 30km. Một ca nô đi xuôi dòng từ bến A đến bến B rồi lại ngược dòng từ B về A. Thời gian ca nô xuôi dòng ít hơn thời gian ca nô ngược dòng là 1h. Tìm vận tốc của ca nô khi nước yên lặng, biết vận tốc dòng nước là 4km/h
Bài 2: Hai bến sông cách nhau 15km. Thời gian ca nô xuôi dòng từ bến A đến Bến B, tại bến B nghỉ 20' rồi ngược dòng từ bến B trở lại bến A tổng cộng là 3h. Tính vận tốc của ca nô khi nước yên lặng, biết vận tốc dòng nước là 3km/h
Bài 3: Một chiếc thuyền đi trên dòng sông dài 50km. Tổng thời gian xuôi dòng và ngược dòng là 4h10'. Tính vận tốc thực của thuyền, biết rằng một chiếc bè thả nổi phải mất 10h mới xuôi hết dòng sông
Bài 4: Hài bến sông A và B cách nhau 40km. Cùng một lúc với ca nô đi xuôi từ A có một chiếc bè trôi từ A với vận tốc 3km/h. Sau khi đến B ca nô trở về A ngay về gặp bè đi đã trôi được 8km. Tính vận tốc riêng của ca nô
CÁC BẠN CHỈ CẦN GỌI ẨN, TÌM ĐIỀU KIỆN VÀ PHƯƠNG TRÌNH THÔI. MÌNH GIẢI PHƯƠNG TRÌNH ĐƯỢC.
Bài 2:
Gọi vận tốc cano là x
Vận tốc cano khi đi là x+3
Vận tốc cano khi về là x-3
Theo đề, ta có: 15/x+3+15/x-3=3-1/3=8/3
=>(15x-45+15x+45)/(x^2-9)=8/3
=>8x^2-72=3*30x=90x
=>8x^2-90x-72=0
=>x=12
1:
Gọi vận tốc cano là x
=>Vận tốc lúc đi là x+4, vận tốc lúc về là x-4
Theo đề, ta co: 30/x-4-30/x+4=1
=>(30x+120-30x+120)/(x^2-16)=1
=>x^2-16=240
=>x^2=256
=>x=16
Đúng 1
Bình luận (0)
Một ca nô xuôi dòng từ A đến B với vận tốc 30km/h, sau đó lại ngược dòng từ B về A. Thời gian đi xuôi ít hơn thời gian đi ngược là 40 phút. Tính khoảng cách AB biết vận tốc dòng nước là 3km/h và vận tốc thật của ca nô không đổi
Gọi khoảng cách giữa AB là x(km).
Thời gian cano đi xuôi là: x/30(h)
Vận tốc cano ngược dòng là 20km
Vậy thời gian di ngược là x/20(h)
Thời gian xuôi ít hơn tg ngược 1h20'=4/3h nên ta có pt x/30+4/3=x/20
x = 80
Đúng 0
Bình luận (0)
1 ca nô đi xuôi dòng trên khúc sông từ A đến B rồi đi ngược dòng từ B trở về A Biết vận tốc dòng nước là 1km/h. Gọi x(km/h) tốc độ của ca nô. Tính vận tốc ca nô biết thời gian đi ít hơn thời gian về là 1 giờ
Một ca nô đi xuôi dòng từ A đến B với vận tốc 50km/giờ. Đi ngược dòng từ B đến A với vận tốc 40km/giờ. Biết thời gian đi xuôi dòng ít hơn thời gian đi ngược dòng là 30 phút? Tính độ dài quãng đường AB?
Tham khảo:
30 phút =0,5 giờ
Giả sử có 2 ca nô cùng khởi hành một lúc thì khi ca nô đi xuôi dòng đến B thì ca nô ngược dòng còn cách A:
40×0,5=20(km)
Hiệu vận tốc xuôi và ngược dòng:
50–40=10(km/giờ)
Thời gian ca nô xuôi dòng hết quãng AB
20:10=2(giờ)
Quãng đường AB:AB:
50×2=100 (km)
Đúng 1
Bình luận (0)





















