Cho hình chữ nhật MNPQ (MN>NP) kẻ MN vuông QN={H}. a.CM:∆MNH~∆NQP. b.CM:MN^2=QN.NH

Những câu hỏi liên quan
Cho hình chữ nhật MNPQ (MN>NP); MH vuông với QN tại H.
a) C/m tam giác MNH đồng dạng với tam giác NQP
b) C/m MN2 = QN.NH
c) Lấy E, F lần lượt là trung điểm của NH,MH. Chứng minh tam giác MNE và tam giác QMF đồng dạng
d) MH cắt PQ tại I. Tính diện tích tam giác MNI, cho QI = \(\frac{1}{2}\)IP và diện tích QHI = 3cm2
Cho hình chữ nhật MNPQ (MN > NP). MH vuông góc với QN tại H.
a) Chứng minh các tam giác MNH và NQP đồng dạng.
b) Chứng minh QN . NH = MN2
c) Lấy E, F lần lượt là trung điểm của NH, MH. Chứng minh tam giác MNE đồng dạng với tam giác QMF.
d) MH cắt PQ tại I. Tính diện tích tam giác MNI, biết QI = \(\dfrac{1}{2}\)IP và diện tích tam giác QHI là 3cm2
a) Xét ΔMNH vuông tại H và ΔNQP vuông tại P có
\(\widehat{MNH}=\widehat{NQP}\)(hai góc so le trong, MN//QP)
Do đó: ΔMNH\(\sim\)ΔNQP(g-g)
Đúng 1
Bình luận (0)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔMNQ vuông tại M có MH là đường cao ứng với cạnh huyền NQ, ta được:
\(NH\cdot NQ=MN^2\)
Đúng 1
Bình luận (0)
Cho hình chữ nhật MNPQ (MN>NP); MH vuông góc QN tại H. Cho QI=1/2IP; diện tích tam giác QHI bằng 3cm vuông. Tính diện tích tam giác MIN
Cho hình chữ nhật MNPQ có MN = 4cm ; NP = 3cm
Vẽ đường cao MH của tam giác MNQ
a, Chứng minh : tam giác MHN đồng dạng với tam giác NQP
b, Chứng minh : MQ2 = QH . QN
c, Tính độ dài đoạn thẳng QH , MH
Cho hình chữ Nhật MNPQ có MN=8cm, NP=6cm. Gọi H là chân đường cao kẻ từ M xuống QN. PE là đường phân giác của góc P
1) chứng minh Tam giác MHN đồng dạng với Tam giác NPQ
2) chứng minh MH.EQ=HN.EN
3) tính diện tích tứ giác MEPH
1: Xét ΔMHN vuong tại H và ΔNPQ vuông tại P có
góc MNH=góc NQP
=>ΔMHN đồng dạng với ΔNPQ
2: EQ/EN=PQ/PN=HN/MH
=>EQ*MH=EN*HN
Đúng 0
Bình luận (0)
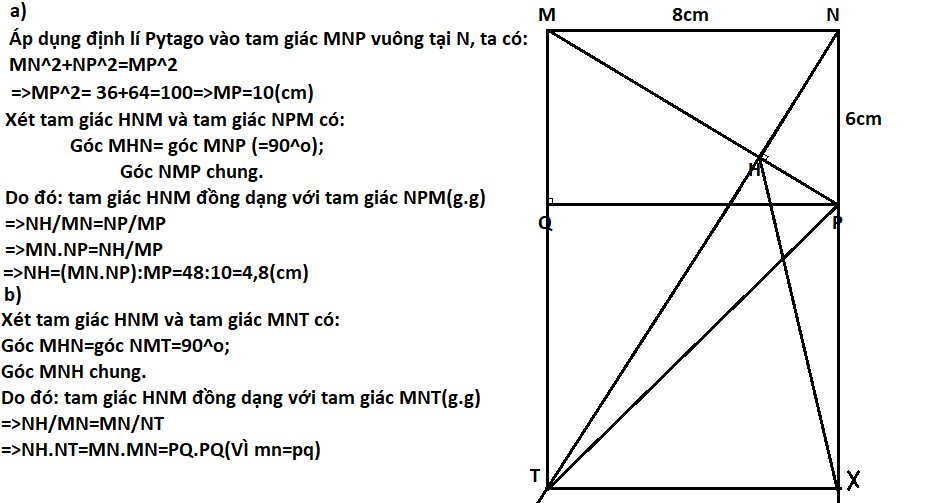
Cho hình chữ nhật MNPQ có MN=8cm, NP=6cm. Kẻ NH vuông góc với MP tại H, tia NH cắt đường thẳng MQ ở T
a. Tính NH
b. Chứng minh NH.NT=PQ.PQ
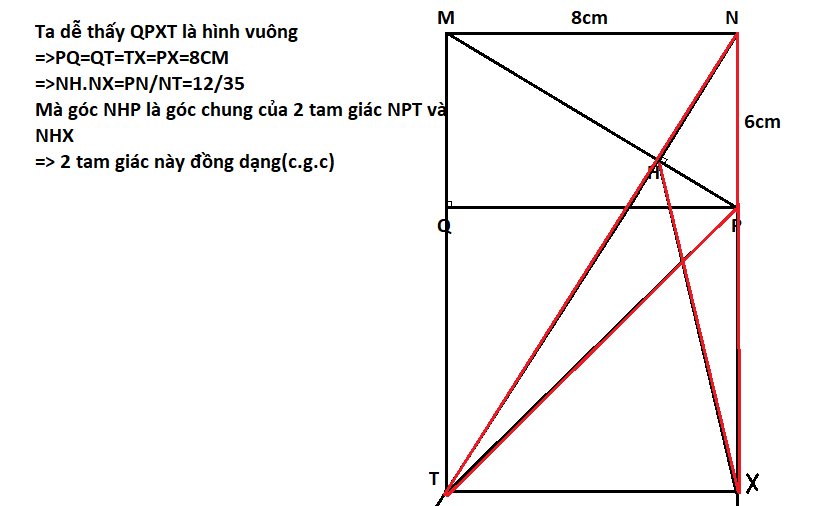
c. Kẻ TX vuông góc với NP tại X. Chứng minh Tam giác NPT đồng dạng với Tam giác NHX
Cho hình vuông ABCD có cạnh AB = 4cm và hình chữ nhật MNPQ có cạnh MN = 2cm, NP = 8cm. Khi đó:
A.Diện tích hình vuông ABCD nhỏ hơn diện tích hình chữ nhật MNPQ
B.Diện tích hình vuông ABCD bằng diện tích hình chữ nhật MNPQ
C.Diện tích hình vuông ABCD lớn hơn diện tích hình chữ nhật MNPQ
D.Không so sánh được diện tích của hai hình
Xem thêm câu trả lời
Cho hình thang cân MNPQ (MN// PQ, MN < PQ), NP = 15cm, đường cao NI = 12cm, QI = 16cm. QN vuông góc NP. E là trung điểm PQ. Đường thẳng vuông góc EN tại N cắt PQ tại K. Chứng minh: KN^2 = KP.KQ.
Cho hình thang MNPQ (MN//PQ) , góc QMN=góc QNP. MP cắt QN tại O.
a. CMR: tam giác MNQ đồng dạng với tam giác NQP.
b.Tính QN, ON,OQ biết MN=9, PQ=16;
c.Có AN là tia phân giác góc MNQ, QB là tia phân giác góc NQP. CMR: AM.BP=AQ.BN=AQ.AQ
d.CMR:AB//MN