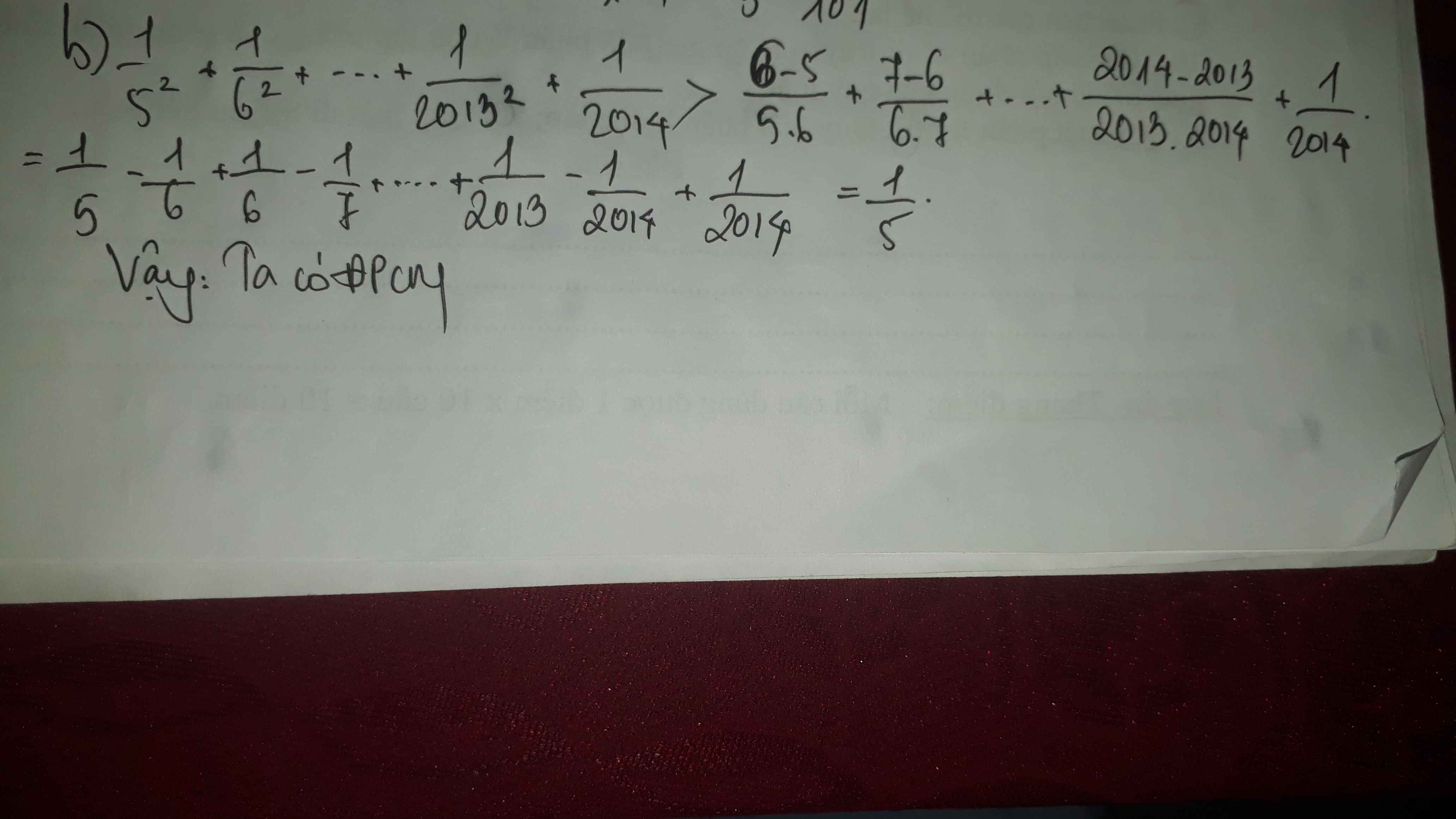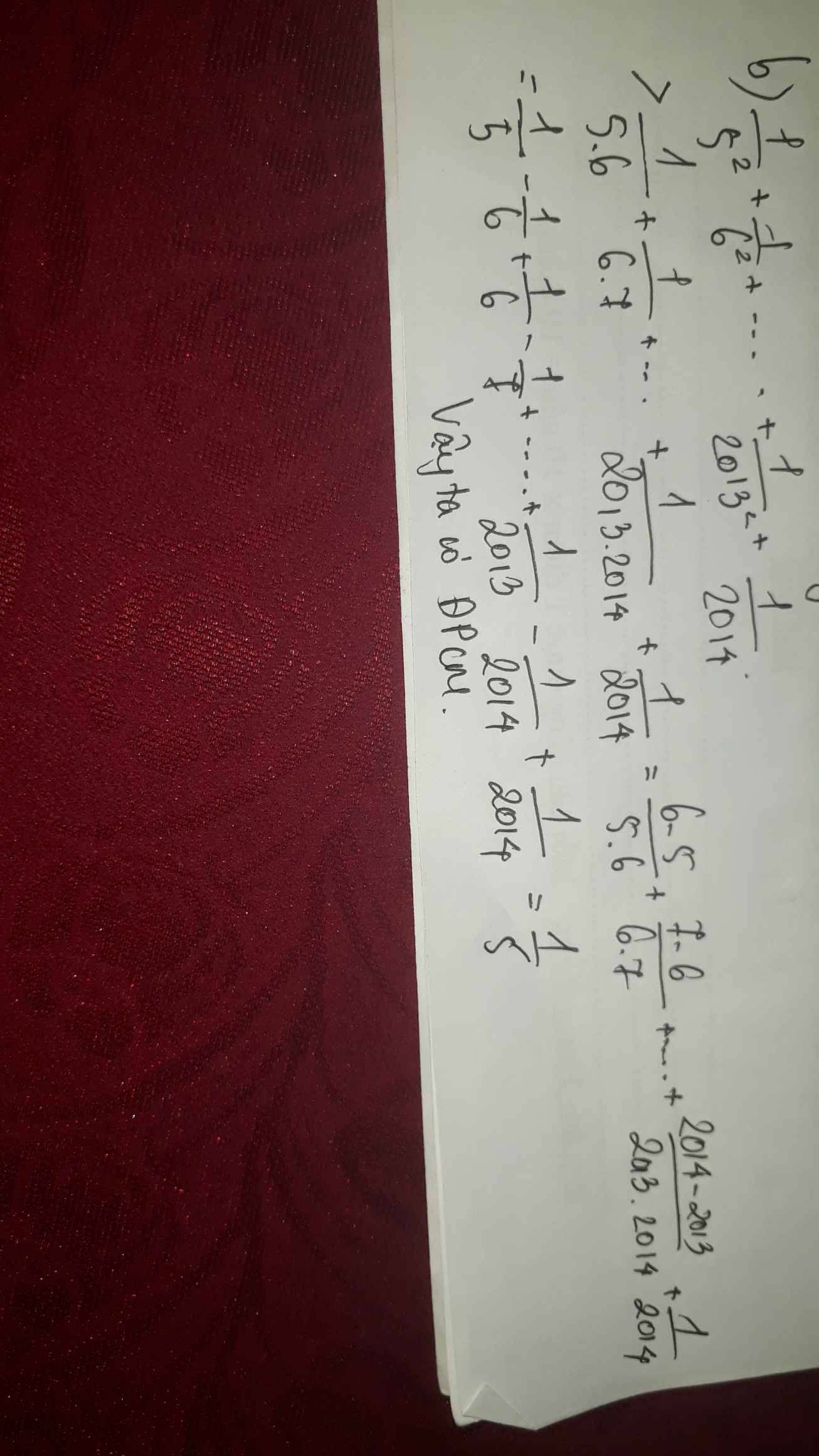B=1/5+1/5^2+1/5^3+...+1/5^2014.Chứng minh B<1/4
Những câu hỏi liên quan
1 Chứng minh
a) A= (-1/5)^0 + (-1/5)^1 + (-1/5)^2 + ..........+(-1/5)^2014 < 5/6
b) B= 1/101 + 1/102 + 1/103 + ....+ 1/200 < 3/4
B=
\(\frac{1}{^{5^2}}+\frac{1}{5^4}+\frac{1}{5^6}+......+\frac{1}{5^{^{2014}}}\)
chứng minh B<1/24
Ta có: \(B=\frac{1}{5^2}+\frac{1}{5^4}+\frac{1}{5^6}+...+\frac{1}{5^{2014}}\)
=> \(25B=1+\frac{1}{5^2}+\frac{1}{5^4}+...+\frac{1}{5^{2012}}\)
=> 25B-B=24B= \(1-\frac{1}{5^{2014}}\)
=> \(B=\frac{1-\frac{1}{5^{2014}}}{24}< \frac{1}{24}\)
=> đpcm
Đúng 0
Bình luận (0)
25 tháng 7 2021 lúc 14:43
chứng minh rằng :
a) \(\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}< \dfrac{1}{4}\) b)\(\dfrac{1}{5^2}+\dfrac{1}{6^5}+...+\dfrac{1}{2013^2}+\dfrac{1}{2014}>\dfrac{1}{5}\)
Cho A = 1/5+1/5^2+1/5^3+...+1/5^2014. Chứng minh rằng A < 1/4
TỪ ĐỀ BÀI => 5A=1+1/5+1/5^2+......+1/5^2013
CÓ 4A=5A-A
=>4A=(1+1/5+1/5^2+.....+1/5^2013)-(1/5+1/5^2+1/5^3+....+1/5^2014)
=>4A= 1- 1/5^2014
=>A= (1-1/5^2014)/4 ;CÓ 1-1/5^2014 <1
=>A<1/4
Đúng 0
Bình luận (0)
\(\text{Giải}\)
\(\text{5A=1+1/5+1/5^2+......+1/5^2013}\)
\(\Rightarrow5A-A=4A=1-\frac{1}{5^{2014}}< 1\Rightarrow A< \frac{1}{4}\left(\text{đpcm}\right)\)
Đúng 0
Bình luận (0)
25 tháng 7 2021 lúc 11:54
chứng minh :
a) \(\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}>\dfrac{1}{4}\) b) \(\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{2013^2}+\dfrac{1}{2014}>\dfrac{1}{5}\)
Chứng minh : 1/2-1/3+1/4-1/5+...+1/2013-1/2014 < 2/5
25 tháng 7 2021 lúc 15:39
chứng minh rằng :
b) \(\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{2013^2}+\dfrac{1}{2014}>\dfrac{1}{5}\)
mọi người ơi chú ý hộ mik là cái chỗ \(\dfrac{1}{2014}\) trên kia là đúng nha
Chứng minh rằng: 1/5+2/52+3/53+4/54+...+2014/52014 < 5/8
CHỨNG MINH 1/2-1/3+1/4-1/5+1/6-1/7+....+1/2012-1/2013+1/2014 < 2/5